Character Table COPY

Question 1

“Mulliken Symbol​”

Meaning: Designates symmetry with respect to inversion center_​

Answer 1

Gerade (symmetric)

Ungerade (Antisymmetric)

Question 2

“Mulliken Symbol​”

In D Point Groups:

Meaning: Designate symmetry with respect to ⊥C_2​

Answer 2

Subscript 1 (Symmetric)

Subscript 2 (Antisymmetric)

Question 3

“Mulliken Symbol​”

In C Point Groups:

Meaning: Designate symmetry with respect to σ_{<span>v</span>}

Answer 3

Subscript 1 (Symmetric)

Subscript 2 (Antisymmetric)

Question 4

Properties of Multiplication Tables

A symmetric multiplication table of a finite group implies the group is _____.

Answer 4

An Abelian Group

Question 5

Properties of Multiplication Tables

Every row and column contains each element exactly once.

True or False

Answer 5

True

Question 6

A group whose elements are all members of another higher order group, both being subject to the same operations.

Answer 6

Subgroup

(Practical use: Building correlation diagrams)

Question 7

Properties of the Character Table

The square of any irreducible representation will include the_____.

Answer 7

Totally symmetric irreducible representation

Question 8

Around the Character Table

Identify the highlighted property of the character table below.

Answer 8

Totally symmetric irreducible representation

Question 9

Around the Character Table

Identify the highlighted property of the character table below.

Answer 9

Mulliken Notation

Question 10

Around the Character Table

Identify the highlighted property of the character table below.

Answer 10

Dimensions

Question 11

Around the Character Table

What is the symmetry of a rotation along the x-axis in a D_3h symmetric molecule?

Answer 11

E’‘

( x and y rotations are degenerate in this case)

Question 12

The D4h molecule [PtCl₄]^2- has a b_1g bending mode:

Applying the the project operator for b_1g yields with θ₁ as the basis:

Pb_1g(θ₁)=N(θ₁ + θ₃- θ₂ - θ₄)

What does the bending motion look like?

Answer 12

Question 13

The facial isomer of MCl₃(CO)₃ has Cl streching modes with the irreducible representations of:

Γ​=A₁+E

How many Cl streching modes are there in MCl₃(CO)₃

Answer 13

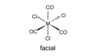
3 Cl streching modes

A₁ (1 mode)

E (2 degenerate modes)

Question 14

What is the subgroup(s) of C_3V based on the multiplication table below?

Answer 14

C₃ (in purple)

C_s (in orange)

Question 15

To have a subgroup g in a higher order group G, the divisor of the orders must be an integral value (e.g h/g )

True or False

Answer 15

True

Question 16

Use the multiplication table below:

C₄*σ_x= ?

Answer 16

σ_d

Question 17

A group whose group operation between two elements does not depend on the order in which they are written.

Answer 17

Abelian Group

Question 18

If a multiplication table’s values are symmetric along its diagonal axis, then that is an _______.

Answer 18

Abelian Group

Question 19

Around the Character Table

What is the symmetry of the dipole moment along the z-axis in a D_3h symmetric molecule?

Answer 19

A₂’‘

Question 20

Around the Character Table

The highlighted operations are ordered in what way?

Answer 20

Classes of Operations

Question 21

Properties of Irreducible Representations

Each irreduible representation is _______ to all other irreducible representation of that group.

Answer 21

Orthogonal

Question 22

Properties of Irreducible Representations

The number of irreducible representations of the group equals____.

Answer 22

The number of classes in a group

Question 23

The characters of all operations in the same class.

Answer 23

Identical

Question 24

Representations that are the combinations of irreducible representations.

Answer 24

Reducible Representations

Question 25

A fundamental representation of a operator’s matrix that cannot be reduced further.

Answer 25

Irreducible Representations

Question 26

What are the characters of the direct product of

(A₁‘)x(A₂”) ?

Answer 26

{1,1,-1,-1,-1,1}

Therefore, the direct product A₂“

(Note: Anything direct producted with the symmetric irreducible representation is itself.)

Question 27

What is direct product of

(E”)x(E’) irreducible representations

in the D_3h point group?

(Note: Will involve a reduction to a sum of irreducible representations)

Answer 27

A₁“+A₂“+E”

Question 28

What is direct product of

(A₂‘)x(A₁“)x(A₂”) irreducible representations

in the D_3h point group?

Answer 28

A₁‘

Question 29

Inspect the multiplication table for C_3v, is this an Abelian group?

Answer 29

Yes

(Symmetric along the diagonal)

Question 30

What is the order of D_3h?

Answer 30

h=12

Question 31

Total number of symmetry operations in the group

Answer 31

Group Order

Question 32

Elements related by a similarity transform_____.

Answer 32

belong to the same class of elements

Question 33

A, B, and X are elements of a group. What does the following operation represent?

X*A*X^-1= B

Answer 33

Similarity Transform

(“ B is the similarity transform of A and X”)

Question 34

“Mulliken Symbol​”

Meaning: Designate symmetry with respect to σ_h

Answer 34

Primes (symmetric)

Double Primes (antisymmetric)

Question 35

“Mulliken Symbol​”

Meaning: Dimension 3

(Triply Degenerate)

Answer 35

T

Question 36

“Mulliken Symbol​”

Meaning: Dimension 2

(Doubly Degenerate)

Answer 36

E

Question 37

“Mulliken Symbol​”

Meaning: Dimension One

Answer 37

A or B

Question 38

Every element of the group must have a reciprocal which is also an element of the group

A*(B*C)=(A*B)*C

Answer 38

Reciprocity

Question 39

The result of an expression is independent of the grouping of the terms

A*(B*C)=(A*B)*C

Answer 39

Associativity

Question 40

One element of the group must, when multiplied in either direction, leave the other elements unchanged.

Answer 40

Identity

Question 41

The product of any two elements of the group or the square any elements, is a member of the group.

Answer 41

Closure

Question 42

A collection of elements that obey the following:

Closure

Contains an Idenitiy

Associativity

Reciprocity

Answer 42

Group