COMP-311 Final Flashcards
2-3 Trees
- 1 to 2 values in each node
- 0 to 3 links to other nodes
- Balanced, non-binary trees
- All leaves are at the lowest level
Approximately, what is the maximum height of a binary search tree of N nodes?
log2 n
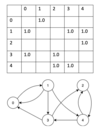
The following items are inserted into a B-tree: 3, 6, 5, 2, 4, 7, 1. Which node is the deepest?
Question doesn’t make sense. Must specify the degree of the B-Tree. Even then, all leaves are at the bottom so there will be many nodes at the “deepest” level.
The following items are inserted into a 2-3 tree: 3, 6, 5, 2, 4, 7, 1. Which node is the deepest?
3, 5
1, 2 | 4 | 6, 7
What operation(s) will require the most time in a balanced binary search tree?
Insertion and deletion have to perform rotations, so they will take longer than search, but they’re all still O(log n).
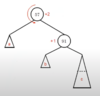
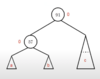
Show the 2-3 tree after inserting each of the following values one at a time: 1, 4, 9
7
3 | 11
7
1, 3 | 11
3, 7
1 | 4 | 11
3, 7
1 | 4 | 9, 11
2-3 Tree Insertion Algorithm
- Find the leaf where the item should be inserted
- If there is only 1 other item in the leaf, put the new item in the leaf
- Otherwise, split the node into two other nodes with the leftmost and rightmost elements, ejecting the middle element up to the parent node.
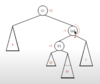
Show the following tree after inserting each of the following one at a time: 9, 13, 17
7
3 | 11, 15
7, 11
3 | 9 | 15
7, 11
3 | 9 | 13, 15
11
7 | 15
3 | 9 || 13 | 17
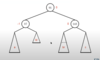
Show the 2-3 tree that would be built for the following sentence: “Rather fail with honor than succeed by fraud.”
rather
fail, rather
rather
fail | with
rather
fail, honor | with
rather
fail, honor | than, with
rather, than
fail, honor | succeed | with
rather
fail | than
by | honor || succeed | with
rather
fail | than
by | fraud, honor || succeed | with
2-3-4 Trees
- Like 2-3 trees, but with another data element and reference
- Node can hold 1-3 data elements
- Node can hold 0-4 references
- Split full nodes upon descent for insertion - ensures that there is always space in a leaf to insert the new item
2-3-4 Trees continued
- 2-3-4 trees are equivalent to Red-Black trees
- 2-node is a black node
- 4-node is a black node with 2 red children
- 3- node is a black node with a read left child or a black node with a red right child (arbitrary choice)
B-Trees
- The natural extension to 2-3-4 trees
- A node holds n data elements and n+1 references to other nodes
- Said to be of degree n
- Algorithms work the same as on 2-3-4 trees
B-Tree Uses
- Disk structures large databases and indexes
- Very high order (200 or more) leads to wide but shallow trees
- Still need to do many comparisons within a node to locate which reference to follow
Selection Sort Algorithm
- Divide array into left (sorted) and right (unsorted) sections
- Find smallest element in the right section
- Swap smallest into first right-side index
- O(n2)
Insertion Sort Algorithm
- Divide array into left (sorted) and right (unsorted) sections
- Pick next element in right section
- Find where it fits in the left section
- O(n2)
Bubble Sort Algorithm
- So long as an exchange takes place
- Loop over all the elements pairwise
- If the elements are out of order, then exchange them
Show the progress of each pass of the selection sort for the following array. How many passes are needed? How many comparisons are performed? How many exchanges?
Original
40 | 35 | 80 | 75 | 60 | 90 | 70 | 75
- # passes: 7 (i.e. n-1)
- # comparisons: 28 (i.e. n * (n-1)/2)
- # exchanges: 7 (i.e. n-1)
Pass1
35 | 40 | 80 | 75 | 60 | 90 | 70 | 75
Pass 2
35 | 40 | 80 | 75 | 60 | 90 | 70 | 75
Pass 3
35 | 40 | 60 | 75 | 80 | 90 | 70 | 75
Pass 4
35 | 40 | 60 | 70 | 80 | 90 | 75 | 75
Pass 5
35 | 40 | 60 | 70 | 75 | 90 | 80 | 75
Pass 6
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Pass 7
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Show the progress of each pass of the bubble sort for the following array. How many passes are needed? How many comparisons are performed? How many exchanges?
Original
40 | 35 | 80 | 75 | 60 | 90 | 70 | 75
- # passes: 4 (varies)
- # comparisons: 22 (varies 7+6+5+4)
- # exchanges: 9 (varies)
Pass 1
35 | 40 | 75 | 60 | 80 | 70 | 75 | 90
Pass 2
35 | 40 | 60 | 75 | 70 | 75 | 80 | 90
Pass 3
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Pass 4
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Show the progress of each pass of the insertion sort for the following array. How many passes are needed? How many comparisons are performed? How many shifts?
Original
40 | 35 | 80 | 75 | 60 | 90 | 70 | 75
- # passes: 7 (i.e. n-1)
- # comparisons: 15 (varies)
- # exchanges: 13 (varies)
Pass 1
35 | 40 | 80 | 75 | 60 | 90 | 70 | 75
Pass 2
35 | 40 | 80 | 75 | 60 | 90 | 70 | 75
Pass 3
35 | 40 | 75 | 80 | 60 | 90 | 70 | 75
Pass 4
35 | 40 | 60 | 75 | 80 | 90 | 70 | 75
Pass 5
35 | 40 | 60 | 75 | 80 | 90 | 70 | 75
Pass 6
35 | 40 | 60 | 70 | 75 | 80 | 90 | 75
Pass 7
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Shell Sort Algorithm
- A better insertion sort
- Sorts parallel sub-arrays
- Decreases gap, and sort larger arrays each pass
- Proven O(n(3/2)) for gaps from 2k-1
- Probably O(n(5/4)) or even O(n(7/6)) for initial gap of n/2, then subsequent gaps dividing by 2.2
Heap Sort Algorithm
- Naive algorithm
- Insert values into a heap
- Repeatedly extract-max
- Can be done efficiently in-place
- Convert array to heap
- For each element: Swap max with last element, Reconvert to a heap
Tree sort algorithm
- Insert values into a binary search tree
- Perform in-order traversal to get sorted list
Merge Sort Algorithm
- “Divide and conquer” algorithm
- Splits list in two
- Sort sub-lists (recursively)
- Merge sub-lists
Quick Sort Algorithm
- “Divide and conquer” algorithm
- Select pivot
- Partition list into:
- items less than pivot
- pivot
- items greater than pivot
- Sort the items on either side of the pivot (recursively)
Show the progress of each pass of the shell sort for the following array. Show the array after all sorts when the gap is 3 and the final sort when the gap is 1. List the number of comparisons and exchanges required when the gap is 3 then 2 and then 1. Compare this with the number of comparisons and exchanges that would be required for regular insertion sort.
Original
40 | 35 | 80 | 75 | 60 | 90 | 70 | 75
Pass 1, Gap 3
40 | 35 | 80 | 70 | 60 | 90 | 75 | 75
Pass 2, Gap 2
40 | 35 | 60 | 70 | 75 | 75 | 80 | 90
Pass 3, Gap 1
35 | 40 | 60 | 70 | 75 | 75 | 80 | 90
Sort the following number using heapsort. What is the efficiency of this algorithm? 55, 50, 10, 40, 80, 90, 60, 100, 70, 80, 20
This is “in-place” O(n log n)
55 | 50 | 10 | 40 | 80 | 90 | 60 | 100 | 70 | 80 | 20
55 | 50 | 10 | 100 | 80 | 90 | 60 | 40 | 70 | 80 | 20
55 | 50 | 90 | 100 | 80 | 10 | 60 | 40 | 70 | 80 | 20
55 | 100 | 90 | 70 | 80 | 10 | 60 | 40 | 50 | 80 | 20
100 | 80 | 90 | 70 | 80 | 10 | 60 | 40 | 50 | 55 | 20
90 | 80 | 60 | 70 | 80 | 10 | 20 | 40 | 50 | 55 | 100
80 | 80 | 60 | 70 | 55 | 10 | 20 | 40 | 50 | 90 | 100
80 | 70 | 60 | 50 | 55 | 10 | 20 | 40 | 80 | 90 | 100
70 | 55 | 60 | 50 | 40 | 10 | 20 | 80 | 80 | 90 | 100
Sort the following numbers using merge sort. What is the efficiency of this algorithm? 55, 50, 10, 40, 80, 90, 60, 100, 70, 80, 20
- recursive and fast [O(n log n)] but requires at least 2n space
- n comparisons to merge output
Original
55 | 50 | 10 | 40 | 80 | 90 | 60 | 100 | 70 | 80 | 20
Split 1
55 | 50 | 10 | 40 | 80 || 90 | 60 | 100 | 70 | 80 | 20
Split 2
55 | 50 || 10 | 40 | 80 || 90 | 60 | 100 || 70 | 80 | 20
Split 3
55 || 50 || 10 || 40 || 80 || 90 || 60 || 100 || 70 || 80 || 20
Merge 1
55 || 50 || 10 || 40 | 80 || 90 || 60 | 100 || 70 || 20 | 80
Merge 2
50 | 55 || 10 | 40 | 80 || 60 | 90 | 100 || 20 | 70 | 80
Merge 3
10 | 40 | 50 | 55 | 80 || 20 | 60 | 70 | 80 | 90 | 100
Merge 4
10 | 20 | 40 | 50 | 55 | 60 | 70 | 80 | 80 | 90 | 100
Sort the following numbers using tree sort. What is the efficiency of this algorithm? 55, 50, 10, 40, 80, 90, 60, 100, 70, 80, 20
- recursive and fast [O(n log n)] if the tree is kept balanced, but requires at least 4n space
Sort the following numbers using quick sort. What is the efficiency of this algorithm? 55, 50, 10, 40, 80, 90, 60, 100, 70, 80, 20
- recursive and fast [O(n log n)] if the pivot is chosen wisely
Original
55 | 50 | 10 | 40 | 80 | 90 | 60 | 100 | 70 | 80 | 20
Pivot 1
20 | 50 | 10 | 40 || 55 || 80 | 90 | 60 | 100 | 70 | 80
Pivot 2
10 || 20 || 50 | 40 || 55 || 80 | 60 | 80 | 70 || 90 || 100
Pivot 3
10 || 20 || 40 || 50 || 55 || 70 | 60 || 80 || 80 || 90 || 100
Pivot 4
10 || 20 || 40 || 50 || 55 || 60 || 70 || 80 || 80 || 90 || 100
Comparison of sorting algorithms
- All O(n2) algorithms are poor. But of these, insertion sort is fastest due to cache hits
- All O(n log n) algorithms are adequate. But of these, quick sort is fast when choosing the pivot well.
What is a graph?
- A graph is an ordered pair (V, E) where V is a set of nodes called vertices, and E is a collection of node paris called edges
- Analogy: vertices are destinations and edges are roads connecting destinations
Directed vs Undirected Graphs
- Undirected graphs: an edge {A, B} implies that there is a connection from A to B and backward from B to A. i.e. the edge is an unordered pair of vertices
- Directed graphs: the edge is an ordered pair, i.e. (A, B) is a “one-way” street leading only from A to B
Draw the undirected graph whose vertex and edge sets are as indicated below:
- Vertices: {A, B, C, D, E, F, G}
- Edges: {{A, E}, {B, G}, {B, C}, {B, A}, {C, E}, {G, D}, {E, F}}
What’s the difference between two graphs?
The directed graph is less connected. For example, there is no path that terminates at B.
Referring to the following graphs, indentify the following when you see them: cycle, weighted graph, directed graph, undirected graph, connected graph, and unconnected graph.
- A cycle is a loop in a directed graph
- A weighted graph has weights associated to each edge, which usually signify some form of cost
- A directed graph has ordered pairs, signifying the direction from one vertice to the other
- An undirected graph an edge is an unordered pair of vertices, signifying a connection in both directions
- A connected graph is when there is an edge to each vertice
- An unconnected graph is where the graph can be separated into two separate pieces, and there are no edges between those pieces
Adjecency Matrix
- Vertices numbered [0..(n-1)]
- 2D array (n * n). Rows represent outgoing edges, columns represent incident edges
- Element at index [i, j] is a number with 1.0 indicating an edge from i to j and 0.0 to infinity representing no edge.
Adjaceny List
- Vertices numbered [0..(n - 1)]
- Array of length n representing source vertices
- Linked list of integers stored at each index representing destination vertices
- Similar in structure to a hash table with chaining
What makes graphs different from most of the other data structures that we have discussed?
Most general structure. Not used to just hold or order data. Represent relationships between elements.
A network of roads and cities: Should it be directed or undirected? Should the edges have weights? If so, what would they mean?
- Undirected
- Weighted with a “cost” of travel
- Cost could be miles, time, or even money (tolls)
Will an undirected and weighted graph adequately represent all road connections?
No, because a directed graph would be required for one-way streets
An electronic circuit with junctions and components: Should it be directed or undirected? Should the edges have weights? If so, what would they mean?
- Digital circuits are directional (have a + & - flow), therefore directed
- Could be weighted, with resistance of the conductor, but unlikely
A frienship graph between people: Should it be directed or undirected? Should the edges have weights? If so, what would they mean? If I am your friend, does that mean you are my friend? How could you tell who has the most friends? What is the largest clique?
- Directed graph A -> B means A considers B a friend. Note A -> B does not imply B -> A
- Could be wieghted with the “strength” of the friendship on a sociological scale (i.e. acquaintance, casual, close, intimate)
- Most friends: most outgoing or most incident edges on a vertex?
- Clique: in graph theory, a clique in an undirected graph G, is a set of vertices V such that for every two vertices in V, there exists an edge connecting the two. This is equivalent to saying that the subgraph induced by V is a complete graph. The size of a clique is the number of vertices it contains.
What is the space complexity for the adjacency matrix implementation?
Space complexity:
- |V|2 => number of vertices squared
- Good when the graph is “dense,” i.e. when |E| ~= |V|2
What is the space complexity for the adjacency list implementation?
Space complexity:
- |E| + |V|
- Good when the graph is “sparse,” i.e. when |E| « |V|2
The following four operations are used extensively in the implementations graph algorithms:
- Find edge (u, v)
- Enumerate all edges
- Enumerate edges emanating from u
- Enumerate edges incident on v
Find the time complexities for each of the operations depending on the implementation (matrix or list) of the graph. Make a chart for comparison.
- Find edge (u, v)
- Adjacency list: O(|Eu|)
- Adjacency matrix: O(1)
- Enumerate all edges
- Adjacency list: O(|E|)
- Adjacency matrix: O(|V|2)
- Enumerate edges emanating from u
- Adjacency list: O(|Eu|)
- Adjacency matrix: O(|V|)
- Enumerate edges incident on v
- Adjacency list: O(|E|)
- Adjacency matrix: O(|V|)
Given a “maze” representation convert it to a graph and demonstrate an algorithm to find a path through the maze.
- Start, end, dead ends, and junctions of 3 or more corridors become vertices
- Apply depth first search or breadth first search to locate the exit
- Observation: the graph is bifrucated
- Result: graph is unconnected
- Conclusion: no path from S to E
Given the following undirected graph, illustrate how breadth-first search works when starting at vertex A:
- V: {A, B, C, D, E}
- E: {{A, B}, {A, D}, {C, E}, {D, E}}
Breadth first: Visit starting vertex, then 1-hop vertices, then 2-hop vertices, etc.
Pass 1
Seen: { A }
Visited: { }
Queue: [A]
Pass 2
Seen: { A, B, D }
Visited: { A }
Queue: [B, D]
Pass 3
Seen: { A, B, D }
Visited: { A, B }
Queue: [D]
Pass 4
Seen: { A, B, D, E }
Visited: { A, B, D }
Queue: [E]
Pass 5
Seen: { A, B, D, E, C }
Visited: { A, B, D, E }
Queue: [C]
Pass 6
Seen: { A, B, D, E, C }
Visited: { A, B, D, E, C }
Queue: []
Illustrate Dijkstra’s algorithm on the following graph. (Dijkstra’s algorithm determines the least-cost path from a source vertex to every other vertex in the graph).
Starting with our initial vertex
S: { 0 }
VS: { 1, 2, 3, 4 }
p: [0, 0, 0, 0, 0]
d: [0, 10, I, 30, 100]
Compare and select the shortest distance. Update distances if shorter distance is found from newly seen vertex, and update predecesor with new vertex.
S: { 0, 1 }
VS: { 2, 3, 4 }
p: [0, 0, 1, 0, 0]
d: [0, 10, 60, 30, 100]
Choose the next shortest distance. Update distances if shorter distance is found from newly seen vertex, and update predecesor with new vertex.
S: { 0, 1, 3 }
VS: { 2, 4 }
p: [0, 0, 3, 0, 3]
d: [0, 10, 50, 30, 90]
Choose the next shortest distance. Update distances if shorter distance is found from newly seen vertex, and predecesor with new vertex.
S: { 0, 1, 3, 2 }
VS: { 4 }
p: [0, 0, 3, 0, 2]
d: [0, 10, 50, 30, 60]
Review the final vertex, and update the distances and predecesors if applicable.
S: { 0, 1, 3, 2 }
VS: { 4 }
p: [0, 0, 3, 0, 2]
d: [0, 10, 50, 30, 60]
Once all vertices have been seen, then the predecesor array will provide the best path to each vertex.
Illustrate Prim’s algorithm on the following graph (Prim’s alogrithm finds a minimum spanning tree)
- Start with original graph
- Will build a new graph
- min-heap with edges
- set of vertices
- set contains everything but starting vertex
- while set is empty, if edge not in the heap, it’s added
- then it will take each edge out of the heap to determine if the vertex has been seen
- then move to the new vertex with the smallest cost
- if the new vertex has edges to vertices we’ve already seen, none of the edges are added, and review the remaining edges (if no destinct smallest, becomes a random choice based on implementation)
u = 0
s = { 1, 2, 3, 4, 5 }
h = [{0, 2}, {0, 3}, {0, 1}]
t = []
u = 2
s = { 1, 3, 4, 5 }
h = [{3, 5}, {2, 1}, {3, 3}, {0, 3}, {0, 1}, {2, 4}]
t = [{0, 2}]
u = 5
s = { 1, 4, 5 }
h = [{5, 3}, {2, 1}, {2, 3}, {5, 4}, {0, 3}, {0, 1}, {2, 4}]
t = [{0, 2}, {2, 5}]
u = 3
s = { 1, 4, }
h = [{2, 1}, {2, 3}, {5, 4}, {0, 3}, {0, 1}, {2, 4}]
t = [{0, 2}, {2, 5}, {5, 3}]
u = 1
s = { 4, }
h = [{1, 4}, {2, 3}, {5, 4}, {0, 3}, {0, 1}, {2, 4}]
t = [{0, 2}, {2, 5}, {5, 3}, {2, 1}]
u = 4
s = { }
h = [{2, 3}, {5, 4}, {0, 3}, {0, 1}, {2, 4}]
t = [{0, 2}, {2, 5}, {5, 3}, {2, 1}, {1, 4}]
Minimum spanning tree is: [{0, 2}, {2, 5}, {5, 3}, {2, 1}, {1, 4}]
Apply DFS, BFS, Prim’s, and Dijkstra’s algorithms to:
One possible DFS:
- (0, 1, 3, 5, 8, 6, 7)
BFS:
- (0, 5, 3, 1, … )
- (0, 5, 3, 1, 10, 8, 6, 4, 2, 11, 9, 7)
Prim’s:
- [{0, 1}, {1, 3}, {1, 4}, {4, 2}, {0, 5}, {5, 8}, {8, 6}, {6, 9}, {9, 7}, {8, 11}, {11, 10}, {9, 12}]
Dijkstra’s
Floyd-Warshall Algorithm
- Works like dijkstra’s, but reviews all possible paths at once
- reviews
- if d[i, j] > d[i, k] + d[k, j]
- If the path from i to j is longer than the path from i to k and k to j, then the latter is shorter
- Sets the new distance, and updates the path
Kruskal’s algorithm
- Spanning tree algorithm, like Prim’s
- Start with a bunch of one vertex graph (each vertex is independent of all the others)
- Take the cheapest edge in the whole graph to connect two vertices - create a union on the sets, so now the vertices are part of the same little graph
- Then take the next cheapest edge
- If an edge is pulled that connects two already connected pieces, it is ignored
- A bunch of little graphs that keep growing, until it creates one large spanning tree
- Works fine as long as there’s a union-find method
Comparing Kruskal’s and Prim’s algorithms
Prim’s good for dense graphs
- Adjacency matrix: O(|V|2)
- Adacjency list: O(|E| + |V| log |V|)
Kruskal’s good for sparse graphs
- Adjacency matrix: O(|V|2 log |E|)
- Adacjency list: O(|E| log |E|)
AVL Trees
- Interested in relative heights of left and right trees (rheight - lheight)
- “Balanced” is when left and right trees differ in height by no more than 1. Recursively, left and right subtrees are also balanced.
Critically unbalanced trees
Four cases:
LL, LR, RR, RL
Left-Left rebalancing
Right- Right rebalancing
Right-Left rebalancing
double rotation
Left-Right rebalancing
Red-Black Trees
- Tree nodes have a color, either red or black
- The root of the tree is black
- Red nodes may not have red children
- The number of black nodes on the paths from every leaf to the root must be the same
- Case one: color new node red - if parent is black, done
- Case two: if parent and uncle are red, color parent and uncle black, color grandpaernt red. Recurse onto grandparent
- Case three: rotate so reds on same side (if necessary), color parent black, grandparent red, rotate again
Red-black insertion
If each branch could only split into two parts at any point, how could Suhai keep the branches and fruit from touching the ground?
By keeping the tree balanced, Suhai could allow the maximum number of fruits to grow before the tree touched the ground
If the room was 10 meters in height, and each branch point could only happen after about a meter branch, roughly how many fruit could the tree produce?
Branch ten times, so 1024
The text gives an algorithm for a right rotation. Describe the algorithm for a left rotation
You can replace right with left everywhere, and it will be the left rotation
Show how the final AVL tree for the “The quick brown fox” changes as you insert “apple,” “cat,” and “hat” in that order.
Build an AVL tree that inserts the integers 30, 40, 15, 25, 90, 80, 70, 85, 15, 72 in the given order
Build the AVL tree from the sentence “Now is the time for all good men to come to the aid of the party.”
Insert the numbers 6, 3, and 0 into the tree
Build the red-black tree from the sentence “Throw your dreams into space like a kite, and you do not know what it will bring back.”
Suppose that the root of a red-black tree is red. If you make it black, does the tree remain red-black? What about the reverse situation?
The root of a red-black tree is always black. Changing it to black might make it a red-black tree. The reverse situation will make the root red, and so it will not be a red-black tree.
What is the largest possible number of internal nodes in a red-black tree with black-height k? What is the smallest possible number?
Largest = 22k - 1
Smallest = 2k - 1
Comparing RB/AVL Trees
- AVL: average height 1.44 log n
- An insert can trigger log n rotations
- RB: average height 2 log n
- An insert triggers constant (amortized) number of rotations or re-colorings
- Conclusion: AVL trees are shorter, but cost more time to keep that way
