Derivatives (Studies) Flashcards
(17 cards)
How are derivatives and tangent lines related?
The derivative is the slope of the tangent line for a given x.
For example, the gradient of the tangent to a function at the point (2,3) will be f’(2).
What is the power rule for finding derivatives?
You bring the exponent down and multiply it in front of its term. Then you reduce the value of the exponent by 1.
For example, if f(x)=-2x2, the derivative is
f’(x)=2*-2x=-4x

What is the derivative of a constant?
0.
When you take the derivative of a constant, that term just disappears.
How do you find the tangent line of a function at a given point (x1,y1)?
- Take the derivative of the function to find f’(x).
- Plug in the x-coordinate for the point they asked you to find the tangent at. (This is the gradient of your tangent line.)
- Since the tangent line is straight, it can be represented as y=mx+c.
- Plug in (x1, y1) from the point you’re given.
- Plug in the gradient you got in the last step.
- Solve for c.
- Write the equation in final form (y=mx+c), but with m and c replaced by their found values.
How do you take the derivative of a function with two or more terms?
For example, f(x)=4x3+2x2-3
You apply the sum or difference rule. The derivative of a function that adds or subtracts two or more terms is the derivative of each term added or subtracted together. You just take the derivative of each term.
For example, f’(x)=8x2+4x.
How are derivatives related to the max/min of a function?
The tangent at the min or max of a function is a flat line, which means its slope is 0. Therefore, the min/max occurs at f’(x)=0.
You find the derivative and then solve for x when f’(x)=0. (This gives you the x-coordinate. To find the y-coordinate, you have to plug this x into the original function.)
What should you do when asked to “minimize”, “maximize”, or “optimize” a function?
- Option 1:
Graph the function on your GDC and use it to find the min/max - Option 2:
- Find the derivative of the function, f’(x).
- Set the derivative to zero, f’(x)=0.
- Solve for x.
- Plug in x from the previous step to find the y-value.
How can you use the derivative to find out on which intervals the original function is increasing/decreasing?
- When the derivative is negative (f’(x)<0), the function is decreasing.
- When the derivative is positive (f’(x)>0), the function is increasing.
What should you do if you are asked to
“find the gradient of the graph of f at x=3 “?
- By hand (and at least written on exam for method marks):
- Take the derivative of f.
- Plug 3 into this function. Make sure to write down “ f’(3) “.
- On the calculator (to double check)

What should you do if you are asked to
Use your answer to a previous part to show that a minimum value of f(x) is -22.
- You must write down “ f’(x)=0”.
- You will have found f’(x) in a previous part. Write down that expression instead of f’(x) on the left side of the equation.
- Solve for x.
- Plug you x-value from step 3 into the original function. You will find that it is -22.
What does this mean?
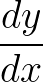
It means derivative. It’s just another way of writing
f’(x).

What are stationary points?
Thye are the points where the derivative equals zero.
All of the solutions to f’(x)=0.
What should you do if asked to:
Find the point on the graph of f at which the gradient of the tangent is equal to 6.
The instant you see “tangent”, you’ll need f’(x).
- Write down f’(x)=6.
- Solve this equation for x.
- Plug this x into the original function to find the other coordinate of the point (x,y).
Why would they tell you this?
The tangent to the graph of y=f(x) at A has equation
y = -2x + 5.
They want you to write down:
- f’(xA)=-2. (xA is the x-coordinate of point A.)
- Solve this equation to find the x-value of A.
How are normal lines and tangent lines related?
They are perpendicular to one another.
Why would they tell you this?

They want you to write down,
f’(2)=21.
In this case, you have an extra variable, k, in your f(x) function and this equation will allow you to solve for it.


