Place Values, Sig. Figs. and Rounding Flashcards
(15 cards)
Why do we round numbers?
Rounding numbers is useful as a way to simplify or estimate an amount. People round numbers in everyday life all the time. Newspapers will talk about 300 people losing their homes as opposed to 287, or someone will mention a currency exchange rate rounded to the nearest euro.
What are the place values?
The place or position of a digit in any number determines its value. For example a 3 on its own only represents a total amount of three items together. But if we put a 0 after it, it becomes a 30. So its position next to the 0 changed its value entirely.
Name the place values to the left of the decimal point.
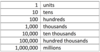
Name the place values to the right of the decimal point.

Why do I need to know the place values?
You need to know what each digit inside any number is called because you can be asked to round off to any one of them for a final answer or for an additional calculation.
Name the place values of each digit in the number
7, 238, 159
7, 238, 159
7 – million
2 – hundred thousand
3 – ten thousand
8 – thousand
1 – hundred
5 – ten
9 – unit
Name the place values of each digit in the number
201.345
201.345
2 – hundred
0 – ten
1 – unit
3 – tenth
4 – hundredth
5 – thousandth
What are the rules for rounding down?
If the number right after the one being rounded off is less than five (0, 1, 2, 3, or 4), we keep that number the same and all the numbers after it become a 0.
e. g. Round 213 to the nearest ten.
The “ten” is the 1 between the 2 and the 3. Look at the digit right after it, the 3. Because it is less than 5, the ten stays the same, but the 3 has to become a zero, because 13 is closer to 10 than it is to 20, so we stick to 10.
So 213 ≈ 210 (to the nearest ten)
What are the rules for rounding up?
If the number right after the one being rounded off is 5 or greater (5, 6, 7, 8, 9), then we round it up to the next integer and everything else after it becomes a 0.
e. g. Round 2,613 to the nearest thousand. The “thousand” is the 2; look at the number right after it, the 6. Because it is greater than 5, the 2 has to round up to 3 and all the other numbers become a zero. When rounding to the nearest thousand, 2,613 is closer to 3,000 than it is to 2,600.
So 2,613 ≈ 3,000 to the nearest thousand
How do we know what number to round off?
You will usually be told, but if no instructions are given, express your final answer to 3 significant figures.
e.g. If you get the result 1,356, rounding off to 3 s. f. would be 1,360.
Round 23,497 to the nearest ten
The “ten” in this case is the 9 in 23,497. So we check if the number right after it is 5 or greater, which in this case it is because it’s a 7. This means we would have to round up the 9 to the next integer - which makes the 400 round up to 500. This answer makes sense, as 23,497 is closer to 23,500 than it is to 23,490.
So 23,497 ≈ 23,500 (to the nearest ten)

What are significant figures?
Significant figures are the digits of a given number that have meaning in an estimate or measurement.
So if we have the number 234.0182736, perhaps the numbers that are most important to us (i.e. are the most significant) are 234, because the decimals are too small to really matter. In this case we say that
234 is our original number
expressed to 3 significant figures (3 s. f.)
Are all numbers (digits) significant?
All numbers are significant except:
- Trailing zeros (these are the zeros that are part of a whole number that come after a digit that is not a zero.) e.g. 4,000 is a number with only 1 significant figure because the 0s don’t count
- Leading zeros (these are the zeros to the left of a whole number.) e.g. 042
Which figures are significant if we have a decimal less than 1?
A decimal less than 1 starts with a 0 followed by a decimal point (e.g. 0.123)
For these decimals, all figures are significant except the leading zeros after its decimal point (i.e. all the zeros before any number that is not 0).
- 0.139kg is less than 1 and has 3 s. f. This is equivalent to 139 grams.
- 0.000936kg is also less than 1 and has 3 s. f. The three zeros between the 936 (i.e. the leading zeros) and the decimal point do not count as significant.
- 0.1003km is less than 1, BUT the zeros between the 1 and the 3 are significant because they are neither leading nor trailing (they are not before the 1, nor after the 3). This number is expressed to 4 s. f. and is the equivalent to 100.3m
Is rounding to a place value different from rounding to a certain number of significant figures?
No, the process is the same. You just need to make sure you don’t miscount the significant figures.
e. g. Round 5647
a) to the nearest hundred, b) to 3 s. f.
a) the hundred in this number is the 6. The number right next to it is a 4 (which is less than 5), so we round down. 5647 ≈ 5600 (to the nearest hundred)
b) 3 significant figures will be the first three digits: 564. Check if the next number is 5 or greater. In this case it is a 7, which means we need to round up.
5647 ≈ 5650 (to 3 s. f.)


