Differentiation

Question 1

In one word,
what is
differential calculus
about?

Answer 1

The
instant.

More specifically, the
rate of change at an instant.

Question 2

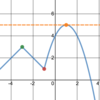
What type of
line
will tell you the
average speed over time?

Answer 2

Secant line.

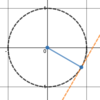
A
slope tells you the
ARC of a
vertical variable
with respect to a
horizontal variable.

ARC is

Δy
Δx

which is also the
slope of the secant line.

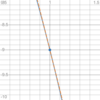
ex:

Δy
Δx

= y₂ − y₁
x₂ − x₁

= 4 − 0
1 − 0

= 4

Question 3

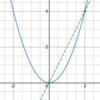
What type of
line
will tell you
instantaneous speed?

Answer 3

Tangent line.

A
slope tells you the
ARC of a
vertical variable
with respect to a
horizontal variable.

The slope of the secant line will approach that of the tangent line as the distances for the secant line approach zero.

Question 4

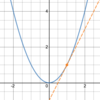
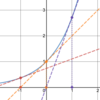
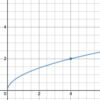
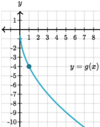
g(x) = √(x)

How can you

• *express** the
• *derivative** of √(x)?

Answer 4

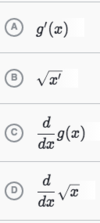
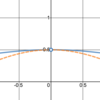
A, C, and D.

Question 5

What is a

• *reasonable** estimate of
• *g’(1)**?

A: −2
B: 1/4
C: 2
D: 0
E: −1/4

Answer 5

−2

Question 6

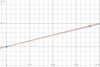
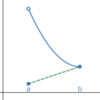
Compare

f(−4) ___ f’(−1).

A: <

B: >

Answer 6

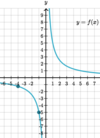
B: >

The slope of the tangent line would be less negative at f(−4).

Question 7

The

• *tangent line** to the graph of
• *function f** at the point
• *(2, 3)** passes through the point
• *(7, 6)**.

What is
f’(2)?

Answer 7

3/5.

The derivative tells you the slope of the tangent.

Δy
Δx

= y₂ − y₁
x₂ − x₁

= 6 − 3
7 − 2

= 3/5

Question 8

What is the

• *formal definition** of the
• *derivative** of a function?

f’(x) = _____?

Answer 8

lim_Δx→0 f(x₀ + Δx) − f(x₀)
Δx

This is basically the slope formula with a limit tacked on:

Δy
Δx

= y₂ − y₁
x₂ − x₁

= lim_Δx→0 f(x₀ + Δx__) − f(x₀)
(x₀ + Δx) − x₀

= lim_Δx→0 f(x₀ + Δx) − f(x₀)
Δx

Question 9

What is the

• *alternate definition** of the
• *derivative** of a function?

f’(x) = _____?

Answer 9

lim_x→a f(x) − f(a)
x − a

This is basically the slope formula with a limit tacked on:

Δy
Δx

= y₂ − y₁
x₂ − x₁

= lim_x→a f(x) − f(a)
x − a

Question 10

How do you write the
equation of a
tangent line using the
formal definition of a
limit of the function below?

f(x) = x² at x = 0.2

Answer 10

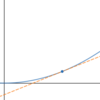
1. Find the derivative
   f(x) = x²
   lim_Δx→0 f(x + Δx) − f(x)
   (x + Δx) − x
   f’(x) = lim_Δx→0 (x + Δx)² − x²
   (x + Δx) − x
   = lim_Δx→0 x² + 2x•Δx + Δx² − x²
   Δx
   = lim_Δx→0 2x•Δx + Δx²
   Δx
   = lim_Δx→0 2x + Δx
   f’(x) = 2x
2. Find the slope of the tangent
   f’(x) = 2x
   = 2(0.2)
   f’(0.2) = 0.4
3. Find the right point on the function
   f(x) = x²
   f(0.2) = (0.2)²
   f(0.2) = 0.04
4. Write the equation of the tangent line
   y − y₀ = m(x − x₀)
   y − 0.04 = 0.4(x − 0.2)

Question 11

Given:

• f(−1) = 2
• f(0) = 0
• f(1) = 1
• f(8) = 5

what is the
best estimate of f’(−1/2) we can make
given these values?

Answer 11

−​2

Δy
Δx

= y₂ − y₁
x₂ − x₁

= 2 − 0
−1 − 0

= −2

Question 12

Given:

• f(−1) = 2
• f(0) = 0
• f(1) = 1
• f(8) = 5

what is the
best estimate of f’(8) we can make
given these values?

Answer 12

4/7

Δy
Δx

= y₂ − y₁
x₂ − x₁

= 5 − 1
8 − 1

= 4
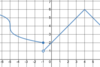
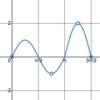
7

Question 13

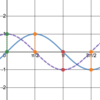
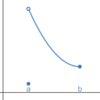
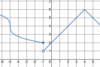
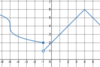
Graphically,
what are
all x-values for which this
function is
not differentiable?

Dashed lines represent asymptotes.

Answer 13

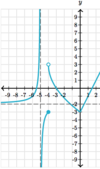
−5, −4, 0

Question 14

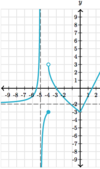
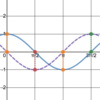
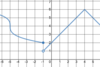
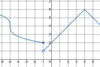
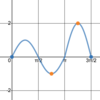
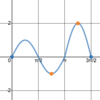
Graphically,
what are
all x-values for which this
function is
not differentiable?

There’s a
vertical tangent at x = 1.

Answer 14

1, 5

Question 15

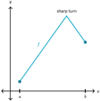
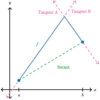
Visually, what
features of a
graph will indicate that
the function is
not differentiable at an x-value?

Answer 15

1. Vertical tangent
   * (the slope of the tangent line is undefined)*
2. Discontinuity
   * (there’s no limit at that location)*
3. “Sharp” turn
   * (the one-sided limits aren’t equivalent, so there’s no limit at that location)*

Question 16

How do you know whether function

• *g(x)** is
• *continuous** at
• *x = a**?

Answer 16

g(x) is continuous at x = a if

• *g(a)** and
• *both one-sided limits** are
• *equal**.
• (Which is to say that the lim_x→a g(x) exists and is equal to g(a).)*
• ex:*

g(x) = { x² + 2x , x < 1
{ 4x − 1 , x > 1

g(1) = (1)² + 2(1)
= 3 = lim_x→1⁻ g(x)

lim_x→1⁺ g(x) = 4(1) − 1
= 3

g(1) = lim_x→1⁻ g(x) = lim_x→1⁺ g(x)

So g(x) is continuous at x = 1.

Question 17

How do you know whether function

• *g(x)** is
• *differentiable** at
• *x = a**?

Answer 17

g(x) is differentiable at x = a
if it is
continuous at x = a and
lim_x→a f(x) − f(a)
x − a
exists.

(Which is to say that you can find the slope of a tangent line that intersects g(x) at x = a)

(Once you know it’s continuous, you’re looking for a
vertical tangent or a
“sharp” turn)

ex:

g(x) = { x² + 2x , x < 1
{ 4x − 1 , x > 1

g(1) = (1)² + 2(1)
= 3 = lim_x→1⁻ g(x)

lim_x→1⁺ g(x) = 4(1) − 1
= 3

g(1) = lim_x→1⁻ g(x) = lim_x→1⁺ g(x)

So g(x) is continuous at x = 1.

lim_x→a f(x) − f(a)
x − a

lim_x→1⁻ x² + 2x − (3)
x − 1

= lim_x→1⁻ (x − 1)(x + 3)
x − 1

= lim_x→1⁻ x + 3

= 4

lim_x→1⁺ 4x − 1 − (3)
x − 1

= lim_x→1⁺ 4x − 4
x − 1

= lim_x→1⁺ 4(x − 1__)
x − 1

= 4

Because the one-sided limits are approaching the same value, the limit exists, and g(x) is differentiable at x = 1.

Question 18

Differentiability
implies _____.

Answer 18

Continuity

Proof:

• Differentiability:
  lim_x→c f(x) − f(c) = f’(c)
  x − c
• Continuity:
  lim_x→c (f(x) = f(c))

Assume f is differentiable at x = c

lim_x→c (f(x) − f(c))

= lim_x→c (x − c) • f(x) − f(c)
x − c

= lim_x→c (x − c ) • lim_x→c f(x) − f(c)
x − c

= 0 • lim_x→c f(x) − f(c)
x − c

= 0 • f’(c)

lim_x→c (f(x) − f(c)) = 0

lim_x→c f(x) − lim_x→c f(c) = 0

lim_x→c f(x) − f(c) = 0

lim_x→c f(x) = f(c)
(this is the definition of continuity)

Question 19

Constant Rule:

Answer 19

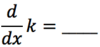
0.

The derivative of
any constant is 0.

Algebraically:

f(x) = 1

f(x + Δx) = 1

g’(x) = lim_Δx→0 f(x + Δx) − f(x)
Δx

f’(x) = lim_Δx→0 1 − 1
Δx

= lim_Δx→0 0
Δx

= 0

Graphically:
The derivative measures a function’s
instantaneous rate of change at a particular x-value.

Where f(x) is a constant, there is
no change from one x-value to the next, so the derivative is 0.

Question 20

Sum/Difference Rules:

f(x) = g(x) + j(x)

f’(x) = ______

Answer 20

g’(x) + j’(x)

f(x) = g(x) + j(x) ⇒ f’(x) = g’(x) + j’(x)

Algebraically:

f(x) = g(x) + j(x)

f’(x) = lim_Δx→0 g(x + Δx) + j(x + Δx) − (g(x) + j(x))
Δx

= lim_Δx→0 g(x + Δx) − g(x) + j(x + Δx) − j(x)
Δx

= lim_Δx→0 g(x + Δx) − g(x) + j(x + Δx) − j(x)
Δx Δx

= lim_Δx→0 g(x + Δx) − g(x) + lim_Δx→0 j(x + Δx) − j(x)
Δx Δx

= g’(x) + j’(x)

The difference rule is identical.

Question 21

Constant Multiple Rule:

• *d [k•f(x)]** = _____?
• *dx**

Answer 21

k• d [f(x)]
dx

Also:
f(x) = k•g(x) ⇒ f’(x) = k•g’(x)

Algebraically:

h’(x) = lim_Δx→0 f(x + Δx) − f(x)
Δx

f(x) = k•g(x)

f’(x) = lim_Δx→0 k•g(x + Δx) − k•g(x)
Δx

= lim_Δx→0 k•g(x + Δx) − k•g(x)
Δx

= lim_Δx→0 k • g(x + Δx) − g(x)
Δx

= k•lim_Δx→0 g(x + Δx) − g(x)
Δx

= k•g’(x)

Question 22

Constant Rule:

f(x) = 2x³ − √x + 1/x + 2

f’(x) = _____

Answer 22

6x² − ½x^−1/2 − x⁻²

*f(x) = x<sup>n</sup>
f'(x) = nx<sup>n−1​</sup>*

f(x) = 2x³ − √x + 1/x + 2

= 2x³ − x^1/2 + x⁻¹ + 2

f’(x) = d/dx(2x³) − d/dx(x^1/2) + d/dx(x⁻¹) + d/dx(2)

= (3)2x³⁻¹ − (½)x^1/2−1 + (−1)x⁻¹⁻² + 0

= 6x² − ½x^−1/2 − x⁻²

Question 23

Power Rule:

f(x) = xⁿ, n ≠ 0

f’(x) = _____

Answer 23

f’(x) = nxⁿ⁻¹

Proof:
(for positive integers)

Question 24

f(x) = 2x³ − √x + 1/x + 2

f’(x) = _____

Answer 24

6x² − ½x^−1/2 − x⁻²

*f(x) = x<sup>n</sup>
f'(x) = nx<sup>n−1​</sup>*

f(x) = 2x³ − √x + 1/x + 2

= 2x³ − x^1/2 + x⁻¹ + 2

f’(x) = d/dx(2x³) − d/dx(x^1/2) + d/dx(x⁻¹) + d/dx(2)

= (3)2x³⁻¹ − (½)x^1/2−1 + (−1)x⁻¹⁻² + 0

= 6x² − ½x^−1/2 − x⁻²

Question 25

How would you write the

• *equation** of a
• *line**
• *tangent** to

f(x) = x³ − 6x² + x − 5

at

x = 1?

Answer 25

1. Find the point the tangent touches
   (this is just f(1))
   f(x) = x³ − 6x² + x − 5
   f(1) = (1)³ − 6(1) + (1) − 5 = −9
   (1, −9)
2. Find the slope of the tangent at that point
   (this is just the derivative)
   f’(x) = 3x² − 12x² + 1
   f’(1) = 3(1)² − 12(1)² + 1
   = −8
3. Write the equation of the line
   y − y₀ = m(x − x₀)
   y + 9 = −8(x − 1) (for point/slope form)
   y = −8x + 8 − 9
   y = −8x − 1 (for slope/intercept form)

Question 26

f(x) = sin(x)

f’(x) = _____

Answer 26

cos(x)

Green: slope of 1

Orange: slope of 0

Red: slope of −1

Question 27

f(x) = cos(x)

f’(x) = _____

Answer 27

−sin(x)

Green: slope of 1

Orange: slope of 0

Red: slope of −1

Question 28

f(x) = e^x

f’(x) = _____

Answer 28

e^x

• This is one of the “magical” things about e.*
• In fact, e can be defined this way.*

Question 29

f(x) = ln(x)

f’(x) = _____

Answer 29

1
x

Question 30

Product Rule:

p(x) = [f₁(x) • f₂(x)]

p’(x) = _____

Answer 30

f₁‘(x) • f₂(x) + f₁(x) • f₂‘(x)

p(x) = [ln(x) • cos(x)]

p’(x) = d/dx(ln(x)) • cos(x) + ln(x) • d/dx(cos(x))

= 1/x • cos(x) + ln(x) • (−sin(x))

= cos(x) − ln(x) • sin(x)
x

Question 31

Quotient Rule:

q(x) = [n(x)]
[d(x)]

q’(x) = _____

Answer 31

n’(x) • d(x) − n(x) • d’(x)
( d(x) )²

q(x) = [sin(x)]
[x²]

q’(x) = d/dx(sin(x)) • x² + sin(x) • d/dx(x²)
(x²)²

= x² • cos(x) − sin(x) • 2x
x⁴

= x (x•cos(x) − 2•sin(x))
x⁴​

= x•cos(x) − 2•sin(x)
x³​

Question 32

f(x) = tan(x)

f’(x) = _____

Answer 32

1 = sec²(x)
cos²(x)

f(x) = tan(x)

= sin(x)
cos(x)
f’(x) = d [sin(x)]
dx [cos(x)]

= cos(x) • cos(x) + sin(x) • sin(x)
cos²(x)

= cos²(x) + sin²(x)
cos²(x)

= 1
cos²(x)

= sec²(x)

Question 33

f(x) = cot(x)

f’(x) = _____

Answer 33

− 1 = −csc²(x)
sin²(x)

f(x) = cot(x)

= cos(x)
sin(x)
f’(x) = d [cos(x)]
dx [sin(x)]

= −sin(x) • sin(x) − cos(x) • cos(x)
sin²(x)

= −sin²(x) − cos²(x)
sin²(x)

= − 1
sin²(x)

= −csc²(x)

Question 34

f(x) = sec(x)

f’(x) = _____

Answer 34

tan(x) • sec(x)

f(x) = sec(x)

= 1
cos(x)

= 0 • cos(x) + sin(x) • 1
cos²(x)

= sin(x)
cos²(x)

= sin(x) • 1
cos(x) cos(x)

= tan(x) • sec(x)

Question 35

f(x) = csc(x)

f’(x) = _____

Answer 35

−cot(x) • csc(x)

f(x) = csc(x)

= 1
sin(x)

= 0 • sin(x) − cos(x) • 1
sin²(x)

= −cos(x)
sin²(x)

= −cos(x) • 1
sin(x) sin(x)

= −cot(x) • csc(x)

Question 36

Chain Rule:

f(x) = o(i(x))

f’(x) = _____

Answer 36

o’( i(x)) • i’(x)

ex:

• h(x) = (5 − 6x)⁵ = o(i(x))
  
  • i(x) = 5 − 6x
    i’(x) = −6
  • o(x) = x⁵
    o’(x) = 5x⁴
• h’(x) = o’(i(x)) • i’(x)
• = 5 ( 5 − 6x)⁴ • −6
• −30( 5 − 6x)⁴

Question 37

Is

f(x) = cos²(x)

a
composite function?

Answer 37

Yes,
so the
chain rule applies.

A function is composite if you can write it as
f(g(x)).

In other words, it is a
function within a function, or a
function of a function.

cos²(x) = (cos(x))² = o(i(x))

i(x) = cos(x)

o(x) = x²

Question 38

f(x) = b^x,
where b is any positive number

d [b^x] = _____
dx

Answer 38

b^x • ln (b)

d/dx [e^x] = e^x​

b = e^{ln (b)}
(remember: log_b a = c ⇔ b^a = c)
(ln (b) is the number that you have to raise e to in order to get b, so if you raise e to that number, you get b)

d/dx [b^x]

= d/dx [(e^{ln (b)})^x] (substitution)

= e^{ln (b) • x} • ln(b) (chain rule)

= (ln (b)) • (e^{ln (b)})^x

= b^x • ln (b)

Question 39

f(x) = log_b a,
where b is any positive number

d/dx [log_b a] = _____

Answer 39

1
(ln b) • a

d/dx [ln x] = 1/x​

Question 40

• *d [y]** = _____?
• *dx**

Answer 40

dy
dx

These are simply equivalent statements.

Question 41

• *d [y²]** = _____?
• *dx**

Answer 41

2y • dy
dx

Just the chain rule:
c(x) = o(i(x))
c’(x) = o’(i(x) • i’(x)

• First, we assume that y does change with respect to x — it’s not a constant.
• Then you can set up y as a function of x:
  y(x)

= d [y²]
dx

= d(y²) • dy
dy dx

↑ This part is just the chain rule:

The
derivative of *something* squared
with respect to that *something*
times the
derivative of that *something*
with respect to x.

= 2y • dy
dx

Question 42

• *d [xy]** = _____?
• *dx**

Answer 42

y + x • dy
dx

Apply the product rule:
p(x) = f₁(x) • f₂(x)
p’(x) = f₁‘(x) • f₂(x) + f₁(x) • f₂‘(x)

• *d [xy]**
• *dx**

= dx • y + x • dy
dx dx

= y + x • dy
dx

Question 43

Given

x² + y² = 1,

how do you obtain

• *dy**?
• *dx**

Answer 43

Implicit differentiation:
Treat the
variable you’re looking for as a
function of the other and
solve.

x² + y² = 1

d (x² + y²) = d (1)
dx dx

d (x²) + d (y²) = 0
dx dx

2x + 2y • dy = 0
dx

2y • dy = −2x
dx

dy = − x
dx y

Question 44

d sin⁻¹ (x) = _____
dx

Answer 44

1
√(1 − x²)

Equivalent statements:
y = sin⁻¹ (x) ⇔ sin(y) = x

x = sin(y)

Derivative of Both Sides w/ respect to x:
dx/dx = d/dx [sin(y)]

1 = d/dy [sin(y)] • dy/dx

1 = cos(y) • dy/dx

_dy_ = _1_ 
 dx cos(y)

Pythagorean trig identity:
dy = 1
dx √(1 − sin²(y))

Substitution:
dy = 1
dx √(1 − x²)

Question 45

d cos⁻¹ (x) = _____
dx

Answer 45

− 1
√(1 − x²)

Equivalent statements:
y = cos⁻¹ (x) ⇔ cos(y) = x

x = cos(y)

Derivative of Both Sides w/ respect to x:
dx/dx = d/dx [cos(y)]

1 = d/dy [cos(y)] • dy/dx

1 = −sin(y) • dy/dx

dy = 1
dx − sin(y)

Pythagorean trig identity:
dy = − 1
dx √(1 − cos²(y))

Substitution:
dy = − 1
dx √(1 − x²)

Question 46

d tan⁻¹ (x) = _____
dx

Answer 46

1
1 + x²

Equivalent statements:
y = tan⁻¹ (x) ⇔ tan(y) = x

x = tan(y)

Derivative of Both Sides w/ respect to x:
dx/dx = d/dx [tan(y)]

1 = d/dy [tan(y)] • dy/dx

1 = 1 • dy/dx
cos²(y)

dy = cos²(y)
dx

Pythagorean trig identity:

= cos²(y)
cos²(y) + sin²(y)

Multiply numerator and denominator by same amount:

= cos²(y) • 1 / cos²(y)
cos²(y) + sin²(y) 1 / cos²(y)

= 1
1 + ( sin(y) / cos(y) )²

Def of tangent:
= 1
1 + tan²(y)

Substitution:
= 1
1 + tan²(y)

Question 47

Functions
f and g are
inverses.

In
terms of its inverse,

f’(x) = _____.

Answer 47

1
g’(f(x))

The
derivative of a function is
equal to the
reciprocal of the
derivative of its
inverse.

• Definitions
  f(x) = g⁻¹(x) ⇔ g(x) = f⁻¹(x)
  f(g(x)) = x = g(f(x))
• Now, the work . . .
  
  • g(f(x)) = x
  • d [g(f(x))] = dx
    dx dx
  • g’(f(x)) • f’(x) = 1
  • f’(x) = 1
    g’(f(x))

Question 48

Given the
table below,
and that
functions g and h are
inverses,

how could you
determine

g’(0)?

Answer 48

g’(0) = 1
h’(g(0))

g’(x) = 1
h’(g(x))

= 1
h’(g(0))

= 1
h’(−2)

= 1
−1

= −1

Question 49

What’s the best way to
evaluate

• *d [(x + 5)(x − 3)]**?
• *dx**

Answer 49

Expand,
then the
product rule.

Expressions can be rewritten to make differentiation easier!

Question 50

What’s the

• *key** to
• *evaluating**
• *d [(x² sin(x))³]**?
• *dx**

Answer 50

Label, label, label.

When applying multiple rules, label them all.

• Rewriting:
  (x² sin(x))³
  = x⁶ sin³(x)
  = f(x) • g(h(x))
• Labeling:
  f(x) = x⁶
  g(x) = x³
  h(x) = sin(x)
• Differentiating:
  f’(x) = 6x⁵
  g’(x) = 3x²
  h’(x) = cos(x)
• d [x⁶ sin³(x)]
  dx
• Product Rule:
  = d [f(x)] • g(h(x)) + f(x) • d [g(h(x))]
  dx dx
• Chain Rule:
  = f’(x) • g(h(x)) + f(x) • g’(h(x)) • h’(x)
• Substitution:
  = 6x⁵ • sin³(x) + x⁶ • 3 sin²(x) • cos(x)
• = 6x⁵ sin³(x) + 3x⁶ sin²(x) cos(x)

Question 51

What’s the

• *key** to
• *evaluating**
• *d [sin (ln (x²))]**?
• *dx**

Answer 51

Label, label, label.

When applying multiple rules, label them all.

• sin(ln(x²)) = f (g (h(x)))
• f(x) = sin(x)
  g(x) = ln(x)
  h(x) = x²
• f’(x) = cos(x)
  g’(x) = 1/x
  h’(x) = 2x
• d [sin(ln(x²))]
  dx
• = f’ (g (h(x))) • g’ (h(x)) • h’(x)
• = cos (ln (x²)) • 1/(x²) • 2x
• = 2 cos (ln (x²))
  x

Question 52

f(x) = x³ + 2x²

f’(x) = 3x² + 4x

f’‘(x) = _____

Answer 52

6x + 4

This is the
second derivative, or the
derivative of the first derivative

Could also be written as:

d²y [x³ + 2x²]
dx²

Question 53

How would you
evaluate

lim_h→0 5 log (2 + h) − 5 log (2)
h

Answer 53

Use the derivative

lim_h→0 5 log (2 + h) − 5 log (2)
h

= 5 lim_h→0 log (2 + h) − log (2)
h

• The above, by definition, is f’(2)*
• So…*
• f(x) = log(x)*

f’(x) = 1
ln(10) x

f’(2) = 1
ln(10) 2

Substitution:
5 • f’(2) = 5 lim_h→0 log (2 + h) − log (2)
h

= 5
2 • ln(10)

Question 54

What is a
related rates problem?

Answer 54

Applied problems where
you find the
rate at which
one quantity is changing by
relating it to
other quantities whose
rates are known.

e.g.:

The radius r(t) of a circle is increasing at a rate of 3 centimeters per second. At a certain instant t₀, the radius is 8 centimeters.

What is the rate of change of the area A(t) of the circle at that instant?

Question 55

What are the

• *keys** to a
• *related rates problem**?

Answer 55

1. Draw a diagram
2. Label, label, label
   Label what you know and what you’re trying to figure out
3. Divide and conquer
   Use information you know to figure out information you need — in several steps if necessary.

Question 56

Given

√(2) = 4,

how might you
approximate

√(4.36)?

Answer 56

Local linearity

You can use the line tangent to at a known point to approximate the value of a value that’s close, but unknown.

Question 57

In words,
What can
L’Hôpital’s rule
do?

Answer 57

Use

• *derivatives** to find
• *limits** with
• *undetermined forms**

This is in contrast to what we normally do, which is to use limits to find derivatives (in fact, the definition of derivatives is based on limits).

Question 58

Mathematically,
what is
L’Hôpital’s rule?

Answer 58

Zero Case:

• If:
  lim_x→c f(x) = 0
  &
  lim_x→c g(x) = 0
  &
  lim_x→c f’(x) = L
  g’(x)
• Then:
  lim_x→c f(x) = L
  g(x)

​Infinity Case:

• If:
  lim_x→c f(x) = ±∞
  &
  lim_x→c g(x) = ±∞
  &
  lim_x→c f’(x) = L
  g’(x)
• Then:
  lim_x→c f(x) = L
  g(x)

Question 59

How would you
evalulate

• *lim_x→0 sin(x)**?
• *2x**

Answer 59

L’Hôpital’s rule

Direct substitution yields:

lim_x→0 sin(x) = 0
2x 0

0/0 is undetermined form.

The first two conditions of the rule are met, so we should try to take the derivatives to see if the third condition is also met.

= lim_x→0 cos(x) = 1
2 2

Therefore . . .

lim_x→0 sin(x) = 1
2x 2

Question 60

How would you
evalulate

• *lim_x→∞ 4x² − 5x**?
• *1 − 3x²**

Answer 60

L’Hôpital’s rule

(is one way, although factoring and canceling would also work)

Direct substitution yields:

lim_x→∞ 4x² − 5x = ∞
1 − 3x² −∞

This is undetermined form.

The first two conditions of the rule are met, so we should try to take the derivatives to see if the third condition is also met.

= lim_x→∞ 8x − 5 = ∞
−6x −∞

This is still undetermined, so we should try L’Hôpital’s rule again:

lim_x→∞ 8 = −4
−6 3

Question 61

Mathematically,
describe the
mean value theorem?

Answer 61

Given that function f is:

• differentiable over the
• open interval (a*, b)** and
• continuous over the
• closed interval [a*, b]**,

There is at least

• *one number c** on the
• *interval** from a to b such that

f’(c) = f(b) − f(a)
b − a

Question 62

Graphically,
describe the
mean value theorem?

Answer 62

An
arc between
two endpoints has a
point at which the
tangent to the arc is
parallel to the
secant through its endpoints

Question 63

Does the

• *mean value theorem**
• *apply** to this function?

Answer 63

No.

For the MVT to apply, the
function must be differentiable
over (a, b).

The function has only two possible tangent lines, neither of which is parallel to the secant between x = a and x = b.

Question 64

Does the

• *mean value theorem**
• *apply** to this function?

Answer 64

No.

For the MVT to apply, the
function must be continuous
over [a, b].

All possible tangent lines are necessarily decreasing, while the secant line is increasing.

Question 65

Does the
mean value theorem
apply to this function
over the interval
[−6, −2]?

There is a vertical tangent at x = −5

Answer 65

No,
because of the
vertical tangent.

The function
must be differentiable
over (−6, −2) for the MVT to apply.

Question 66

Does the
mean value theorem
apply to this function
over the interval
[−4, −1]?

There is a vertical tangent at x = −5

Answer 66

Yes.

The function is
continuous over [−4, −1] and
differentiable over (−4, −1).

Question 67

Does the
mean value theorem
apply to this function
over the interval
[−1, 2]?

There is a vertical tangent at x = −5

Answer 67

No.

The function
must be continuous
over (−1, 2) for the MVT to apply.

Question 68

Does the
mean value theorem
apply to this function
over the interval
[0, 4]?

There is a vertical tangent at x = −5

Answer 68

Yes.

The function is
continuous over [0, 4] and
differentiable over (0, 4).

Question 69

Does the
mean value theorem
apply to this function
over the interval
[0, 5]?

There is a vertical tangent at x = −5

Answer 69

No,
because of the
“sharp” turn.

The function
must be differentiable
over (0, 5) for the MVT to apply.

Question 70

Mathematically,
describe the
extreme value theorem?

Answer 70

Given that function f is:

• *continuous** over the
• closed interval [a*, b]**,

There are
values c and d
in the interval [a, b] such that
f(c) < f(x) < f(d).

Question 71

Graphically,
describe the
extreme value theorem?

Answer 71

Where function f is
continuous over [a, b],
there is an
absolute maximum value of f over the interval
and an
absolute minimum value of f over the interval.

Question 72

Visualize why an
interval must be continuous
for the
extreme value theorem to apply.

Answer 72

Question 73

Visualize why an
interval must be closed
for the
extreme value theorem to apply.

Answer 73

Question 74

What is a
critical point?

Answer 74

An x-value:

• within the domain of function f (graphed below)
• where
  
  • f’(x) = 0
    or
  • f’(x) is undefined

Green is local max — f’(x) is undefined
Red is local min — f’(x) is undefined
Orange is global max — f’(x) is zero

Question 75

How do you find an
increasing or decreasing interval
of a function?

Answer 75

Differentiate
and evaluate
around critical points.

f’(x) will be
positive where f(x) is increasing
and
negative where f(x) is decreasing.

Question 76

How do you find
global/absolute extrema?

(aka the first derivative test)

Answer 76

Same as local/relative extrema,
except you must
check the edges
in both directionsbecause
endpoint can be global/absolute extrema.

• Differentiate
• Find
  
  • critical points
    and
  • where f(x) is undefined
• Analyze intervals using first derivative
• Find extremum points, which will be where
  
  • f(x) is defined
    and
  • f’(x) changes signs
• Check edges

Question 77

How do you find
local/relative extrema?

(aka the first derivative test)

Answer 77

• Differentiate
• Find
  
  • critical points
    and
  • where f(x) is undefined
• Analyze intervals using first derivative
• Find extremum points, which will be where
  
  • f(x) is defined
    and
  • f’(x) changes signs