Entrepreneurial Firm

Question 1

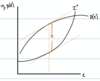
Draw Scitovsky’s diagram for an entrepreneurial firm and explain it.

Answer 1

• I⁰ = inndifference curve - shows opportunity cost of effort in the firm
• y = p(e) = gross income from effort
• π = economic profit = rev - opp cost
  *

Question 2

Show that the owners indifference curve is upward sloping.

Answer 2

• U = U(e,y)
• U_e < 0, U_ee < 0
• U_y > 0, U_yy < 0
• find ^dy/_de using implicit fn theorum
• prove its value is >0
  *

Question 3

How does an entrepreneur maximise profits in the skitovsky model?

Answer 3

• π = p(e) - A(e,u⁰)
• F.O.C: ^dπ/_de = p_e(e) - A_e(e,u⁰) = 0

This rearranges into: p_e(e) = A_e(e,u⁰)

The revenue slope = the indifference curve slope

Question 4

How does an entrepreneur maximise utility in the skitovsky model?

Answer 4

• Lagrangean max U(e,y) s.t. y=p(e)
• Solution : p_e(e*) = - ^U_e/_Uy

Optimal at tangency

Question 5

Explain Skitovsky’s condtion

Answer 5

• Utility max can only equal profit maximisation point if I⁰ is the same shape as I¹
  
  • ​income must have no impact on preferences for effort
  • Quasi linear preferences
  • U_ey = 0

How likely is it?

1. Leisure is a normal good so prefs would change
2. Work is an investment in human capital so changes over time
3. HH and family concerns alter preferences
4. tax creates distortion

Question 6

Explain the basic principles of the input market

Answer 6

The owner can seperate effort into their own firm and into the market

e_F = effort into firm, e = total effort from owner

manager can be hired to spend effort in firm

firm profit = π = p(e_F) - w(e_F)

Owners utility = U(e,y) = U(e, [π(e_F) + we])

Question 7

How do you maximise utility and profit in the input market?

Answer 7

• max U(e,y) = U( e, [p(e_F) - we_F +we] )
• Utility max: ^dU/_de = U_e + U_yw = 0
• w = - ^Ue/_Uy wage slope = idc slope
• Profit max
• ^dU/_def = U_y.U_ef = U_y ( p’(e_F) - w) 0
• p’(e_F) = w
• Wage = revenue slope (max gap)