Exam III Flashcards
(24 cards)
Fundamentally, how do spectroscopic techniques work?
They rely on the ineraction between matter and electromagnetic radiation
I
Nuclei often act as a single entity with intrinsic angular momentum I.
A characteristic of the collection of protons and neutrons (which are fermions) is that a nucleus of odd mass number A will have a half-integer spin and a nucleus of even A will have integer spin. The suggestion that the angular momenta of nucleons tend to form pairs is supported by the fact that all nuclei with even Z and even N have nuclear spin I = 0. For example, in the nuclear data table for iron below, all the even A nuclides have spin I = 0 since there are even numbers of both neutrons and protons. The half-integer spins of the odd-A nuclides suggests that this is the nuclear spin contributed by the odd neutron

When does I = 0?
Even atomic mass (A: protons + neutrons) and even number (Z: protons)
Even A
Even Z
12C, 16O
When does I = whole integer?
Even atomic mass (A: protons + neutrons) and odd number (Z: protons)
Even A
Odd Z
14N, 2H, 10B
When does I = half integer?
Odd atomic mass (A: protons + neutrons)
Odd A
Even or odd Z
1H, 13C, 15N, 31P
Lamor frequency
The Larmor frequency depends on a quantity known as the gyromagnetic ratio, γ , the chemical shift δ, and the strength of the applied magnetic field, B0:
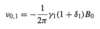
γ
Gyromagnetic ratio, γ, (rad⋅s−1⋅T−1) of a particle is the ratio of its magnetic moment to its angular momentum.
Most common nuclei such as 1H and 13C have positive gyromagnetic ratios.
1H γ = 267.513 (106 rad s−1 T −1)
13C γ = 67.262 (106 rad s−1 T −1)

What is the energy differential between α and β spin states in a 1-spin system when B0 = 0?
No difference in energy states when B0 = 0, they are degenerate.
Notice when B0 = 0, ν0,1 = 0 so Eα = Eβ —> ΔE = 0
What is the energy differential between α and β spin states in a 1-spin system when B0 > 0?
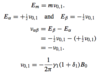
Selection Rule
In the case of NMR, the selection rule refers to the quantum number m: only transitions in which m changes by one (up or down) are allowed. This is sometimes expressed as:

What happens to nuclear spins outside of a magentic field?
They exist in the ground state, no energy difference between spins and so the spins are disordered. They are degenerate.
What happens to nuclear spins when a magentic field is applied?
In a magnetic field at equilibrium, the magnetic moments are not aligned randomly but in such a way that when their contributions are all added up there is a net magnetic field along the direction of the applied field (B0). This is called the bulk magnetization of the sample.
The magnetization can be represented by a vector – called the magnetization vector – pointing along the direction of the applied field (z)

Express the angular velocity of a nuelcus, ω0, in terms of an applied magnetic field strength B0
ω0 = -γB0
Express the angular velocity of a nuelcus, ω0, in terms of the Larmor frequency, ν0
ω0 is in rad s-1
ν0 is in Hz
Hz * 2π = rad s-1
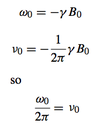
How do you calculate the ratio of the α/β spin level populations?
Boltzmann distribution
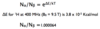
What part of the EM specrum does NMR fall into?
Radiofrequency
~400MHz 1H
~100MHz 13C

If you measure the peak of TMS on one machine as 400 MHz, and you move to another machine with twice the magnetic field strength, what frequency will TMS absorb?
800 MHz
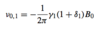
Conceptually, what is the vector model?
Classical simplification that is a very visual way of comprehending the results of pulses and delay times in many modern nmr experiments.
At equilibrium the magnetic moments are not aligned randomly, but in such a way that when their contributions are all added up there is a net magnetic field along the direction of the applied field (B0). This is called the bulk magnetization of the sample.
The magnetization can be represented by a vector – called the magnetization vector – pointing along the direction of the applied field (z). In the vector model we will only be concerned with what happens to this vector.
Vector model: isotropic spin distribution
If the addition of the magnetic moments results in a net magnetic moment of 0 (due to random spin orientation) then we can say that the spin distribution is isotropic.
Isotropic: (of a property or phenomenon) not varying in magnitude according to the direction of measurement.
Vector model: What happens immediately after a sample is placed into a magnetic field?
Immediately after entering the field, the spins begin precessing about the external magnetic field (B0, by convention about the z-axis).
A sample of normal concentration would contain on the order of 1016 spins, all precessing out-of-phase with μ (mag moment) pointing in random directions.
Immediate addition of these μ vectors upon entering the field will result in a net magnetic moment of 0.
When μnet = 0, spin distribution is isotropic
Vector model: anisotropic spin distribution
When the spin component vectors add up to give a net magnetisation along an axis we say that the spin distribution is anisotropic.
Anisotropy: (of a property or phenomenon) varying in magnitude according to the direction of measurement.
Rotating coordinate frame
Uses a moving coordnate frame to reduce the time component of the magnetic motion vector.
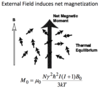
M0
The net magnetic moment of the sample from an external magnetic field.
N – number of spins, γ – gyromagnetic ratio, ħ – Planks constant, I – spin quntum number, μ0 – permeability of free space, B0 – Applied magnetic field strength (induction), K - Boltzman constant, T – temperature.