Finals Flashcards
degrees → radian
degree • pi/180
radians → degree
radian • 180/pi
evaluate sin x, cos x, and tan x for a value x
- if necessary, convert x to degrees
- Check what quadrant it’s in
- Do whatever the quadrant says to do
- Use special/quadrantal angles tables to solve
special angles table
quadrantal angles table
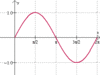
y = sin x graph → 0 1 0 -1 0
y = cos x graph → 1 0 -1 0 1
tan x = sinx/cosx
state the number of revolutions for an angle
- convert to radians
- radians/2pi
convert to decimal degree form
Ex: 152o15’29”
152 + (15/60) + (20/3600) =
152.26o
decimal degree form
156.33o
DMS form
122o25’51”
convert to DMS form
Ex: 24.240
24o(.24*•60)’ (.4**•60)”
24o14’24”
*.24 is from 24.24
**.4 is from (.24•60 = 14.4)
1’ = ?
one minute = (1/60)(1o)
1” = ?
one second = (1/60)(1’) = (1/3600)(1o)
quadrant rules
terminal ray
the pipe cleaner
in which quadrant does the terminal side of each angle lie when it is in standard position?
- convert to degrees
- if negative, + 360; if over 360, - 360
- find which quadrant it’s in
find the exact value of sin/cos/tan x. no calculator.
- if radians, convert to degrees
- use quick charts
use a calc to approximate sin/cos/tan x to four decimal places
- if degree, change calc to Degree mode
- if radians, change calc to Radians mode
sketch w/out a calculator a sin/cos/tan curve
xmin = -2pi
xmax = 2pi
xscl = pi/2 (unless stated otherwise)
ymin = -5
ymax = 5
yscl = .5
sin, cos
- if y = c + cos(x) → period & amplitude same; c = pos moves max/min up, c = neg moves max/min down
- if y = a sin(x) → period same; move max to a
- if y = sin(bx) → max/min/amp same; normal period/b
- if y = sin(x + b) → if b = pos, move left; if b = neg, move right
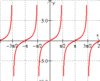
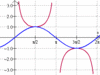
**tan, cot, sec, csc - **no ampl/min/max
- y = c + tan(x) → if c = pos, move up; c = neg, move down (easier to just move x-int’s)
- y = a csc(x) → move min/max’s to a
- y = cot(bx) → period/b
period
- for sin, cos curves → the shortest distance along the x-axis over which the curve has one complete up-and-down cycle
- for tan, distance b/w consecutive x-intercepts
amplitude
max - min
vertical asymptotes
lines that the graph approaches but doesn’t cross
periodic
repeating
Ex: tan function
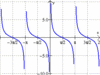
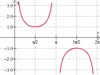
csc, sec, cot
csc = 1/sin
sec = 1/cos
cot = 1/tan
what happens to y = csc(x) whenever y = sin(x) touches the x-axis?
vertical asymptote
why are y = sin(x) and y = csc(x) tangent whenver x is a multiple of x
they r reciprocals, so csc’s max is at sin’s min, and csc’s min is at sin’s max
sine function: y = sin(x)
“wave”
amplitude - 1
period - 2pi
frequency = 1 cycle in 2pi radians (1/2pi)
max - 1
min - (-1)
one cycle occurs between 0 and 2pi with x-int @ pi
cosine function: y = cos(x)
also “wave”
amplitude = 1
period = 2pi
period = 2pi
frequency = 1 cycle in 2pi radians (1/2pi)
max = 1
min = -1
one cycle occurs b/w 0 & 2pi w/ x-int’s @ pi/2 & 3pi/2
tangent function: y = tan(x)
amplitude = none, go on forever in vertical directions
period = pi
one cycle occurs b/w -pi/2 and pi/2 (x-int = 0)
cotangent function: y = cot(x)
amplitude = none
period = pi
one cycle occurs b/w 0 and pi (x-int pi/2)
relationship b/w tan & cot graphs
the x-int’s of y = tan(x) are the asymptotes of y = cot(x)
and vice versa
cosecant function: y = csc(x)
amplitude = none
period = 2pi
one cycle is between 0 & 2pi, with the center being @ pi/2
relationship b/w sin & csc graphs
the maximum values of y = sin(x) are min values of the pos sections of y = csc(x)
the min values of y = sin(x) are the max values of the neg sections of y = csc(x)
the x-int’s of y = sin(x) are the asymptotes for y = csc(x)
secant function: y = sec(x)
amplitude = none
period = 2pi
one cycle occurs between -pi/2 and pi/2, with the center being at 0
relationship b/w cos & sec graphs
the max values of y = cos(x) are the min values of the pos sections of y = sec(x)
the min values of y = cos(x) are the max values of the neg sections of y = sec(x)
the x-int’s of y = cos(x) are the asymptotes for y = sec(x)
algorithm
a set of step-by-step directions for a process
simple sequence of steps that u follow in order
loop
a group of steps that r repeated for a certain # of time or until some condition is met
solving algorithms in two ways
- algebra - just solve
- graph - for inequalities
- graph both sides of equation separately
- estimate x-coord of intersection
- Ex: - 3x + 9 < 4
- all values of x for which y = -3x + 9 is BELOW y =4 (remember to use sign! and flip if necessary!!)
box and whisper plot
gives data in 4 parts - each part = 25% of the data
scatter plot
break-even point
when income = expenses
- separate expenses from income
- write equations to model the situation for I and E
- find break-even point, when I = E
- use a graph
- graph the equations on same set of axes
- x-coord of itnersection = BEP
- use algebra
- use a graph
matrices
x + y = 10,000
7x + 15y = 86,000
[A] [xy] = [B]
A = coefficient matrix, B = constant matrix
[17115] [xy] = [10,00086,000]
use calc 2nd matrix → edit
[A]-1 [B]
linear equation with 3 variables
ax + by + cz = d
assigning
- connect
- look for something that connects with only one other thing
- narrow down
diagramming
- put the thing w/ the most things in the center
- when 2 vertices r connected by 2+ edges, draw @ least 1 edge as a curved line
- draw arrows to show “direction”
matrixing
each row = departure
each column = destination
1 = on, 0 = off
vertex of a network
a dot in the network
edge of a network
line connecting 2 dots in a network
maximizing and minimizing
x-value of vertex = -b/2a
finding the shortest route
- Draw a network diagram that models the map. Each vertex represents a city. Each edge represents an interstate highway. Distances do not need to be drawn to scale.
- Label the starting point with the ordered pair (-,0)
- For each edge that connects a labeled and an unlabeled vertex, find this sum:
- s = y-value of ordered pair for labeled vertex + length of edge
- Choose the edge from Step 3 that has the minimum sum s. Label the unlabeled vertex of that edge with this:
- (label of the other vertex of the edge, s)
- Repeat Steps 3 & 4 until the vertex for the destination is labeled. (Go all the way back to find shortest distance).
- When the vertex for Danville is labeled, use the ordered pairs to find the shortest route. (backtrack)
constraint
any condition that must be met by a variable or by a linear combination of variables
x > 0 → The # of AM ads can’t be negative
y > 0 → the # of PM ads can’t be negative
x + y < 20 → the total # of ads must be less than/equal to 20
200x + 50y < 2200 → the total cost of the ads must be less than or equal to $2200
feasible region
the graph of the solution of a system of inequalities that meets all given constraints
graphing feasible regions
use system of inequalities from “constraint” definition
- Since x > 0 and y > 0, the feasible region is in the first quadrant.
- Graph x + y < 20 in the first quadrant.
- Identify points inthe blue shaded region that also make 200x + 50y < 2200 true.
- The feasible region consists of all pts on or inside quadrilateral ABCO. u can find the coord’s of each vertex by solving a system of equations from the intersecting lines
- the origin (0,0) is the solution of the system: x = 0, y = 0
- solve this system: x + y = 20, x = 0 to get (0,20)
- Solve x + y = 20, 200x + 50y = 2200 to get (8,12)
- solve 200x + 50y = 2200, y = 0 to get (11,0)
linear programming
can be used
- when u can represent the constraints on the variables with a system of linear inequalities
- when the goal is to find the max/min value of a linear combo of the variables
corner-point principle
any max/min value of a linear combo of the variables will occur at one of the vertices of the feasible region
using the corner-point principle
AM ads heard by 90,000; PM ads heard by 30,000
@ most 20 ads, @ least as many AM ads as PM ads, at least 720,000 listeners
hows many of each ad should u run to minimize the total cost? how much will the ads cost?
- Represent the constraints with a system of linear inequalities
- Let x = the number of AM ads, y = # of PM ads
- x + y < 20
- x > y
- 90,000x + 30,000y > 720,000
- x > 0
- y > 0
- Graph and find vertices
- Write a linear combo that represents the total cost of the ads: 200x + 50y
- Use the corner-pt principle. Find the total cost for the combo of ads represented by each vertex.
- min turns out to be A(6,6)
even function
a function if its graph = symmetric w/ respect to y-axis
f(-x) = f(x)
odd function
a function if its graph is symmetric with respect to the origin
turn upside down to test - 180o
f(-x) = -f(x)
holes
when a value of x sets both the denom & the numer of a rational function equal to 0, there is a hole in the graph
a single pt in which the function has no value
to find:
f(x) = (x2[x-2])/(x-2)
look for repeating thingies like x -2
therefore, x = 2
finding asymptotes, holes, 0’s, x-int’s, & y’int’s
f(x) = x2+x-6 / x+3
- vertical asymptote
- set denom to 0
- x + 3 = 0 → x = -3
- holes
- factor out the numerator to (x+3)(x-2)
- x+3 is found on both the num & denom
- therefore, x = -3
- zeros (where y = 0)
- set f(x) to 0 and solve for x
- x-int’s → same as zeros
- y-int (where x=0)
- set all x’s to 0 and solve
control variable
a variable that determines, or controls, another variable
x
domain
dependent variable
a variable that is determined by, or depends on, another variable
y
range
function
a relationship for which each value of the control variable is paired with only one value of the dependent variable
domain
all possible values of the control variable
x-axis
range
all possible values of the dependent variable
y-axis
values of a function
the numbers in its range
vertical line test
if no vertical line crosses a graph in >2 points, the graph represents a function
one-to-one function
a function in which each member of the range = paired with exactly one member of the domain
horizontal line test
if no horizontal line crosses the graph, it’s
- a one-to-one function
- has an inverse
many-to-one function
a member of the range may be paired with more than 1 member of the domain
linear function
a function that has an equation of the form f(x) = mx + b, where m is the slope of its linear graph & b is the y-intercept
domain = all real #’s
range = all real #’s
f(x) = x + b → pos moves left, neg moves right
f(x) = mx → 0 < m < 1 less steep, m > 1 more steep
f(x) = -x → reflection
slope
change in f(x)
____________
change in x
long division
if no 3a, would still have to put 0a!!!
synthetic division
ignore green
inside numbers from coefficients
once have an x2 in answer, just factor normally to get x
degree
greatest power
horizontal asymptotes
- if degree of num > degree of denom → NO hor. asympt.
- n < d → hor. asympt. at y = 0 (x-axis)
- if n = d, there is hor. asympt. @ y = an/bm where an = leading coeffcient of num & bm = leading coefficient of denom.
piecewise function
a function defined by 2+ equations
each equation applies to diff part of the function’s domain
Ex:
1/2lb or less → $13
more than 1/2 lb but less than 1 lb → $20
1lb + → $25
w = weight, c(w) = charge
c(w) = {13 if 0 < w < 1/2
{20 if 1/2 < w < 1
{25 if 1 < w
absolute value functions
|x| = x if x > 0; -x if x < 0
f(x) = |x| + b → pos moves up, neg moves down
f(x) = |x - 3| → neg moves right, pos moves left
f(x) = m|x| → 0 < m < 1 less steep, m > 1 more steep
f(x) = -|x| → reflection
graph: y = |x + 2|
y = x + 2 if x + 2 > 0 → x > -2
-(x + 2) if x + 2 < 0 → x < -2
Graph y = x + 2 and y = -(x + 2)
quadratic functions
f(x) = ax2 + bx + c
where a, b, and c are constants and a doesn’t equal 0
parabola
sign of a determines whether parabola opens upward or downward
f(x) = x2 + b → pos. up, neg. down
f(x) = (x - c)2 → c neg move right, pos. move left
f(x) = ax2 → same as others
f(x) = -x2 → same as others
height and distance formulas
t = time, v0 = initial speed, A = angle at which obj is thrown, h0 = initial height
distance fallen d(t) = 16t2
height after being thrown h(t) = -16t + (v0 sin A)t + h0
distance problems
a person drops a penny from a height of 50ft. express height of penny above ground as a function of time
let h(t) = height after t secs
(distance fallen) + (height above ground) = (initial height)
16t2 + h(t) = 50ft
h(t) = -16t2 + 50
domain = 0 < t <
range = 0 < h(t) < 50
height problems
lacrosse: ball leaves player’s stick from initial height of 7ft @ speed of 9ft/s & @ angle of 30o w/ respect to horizon
1. express height of ball as function of time
h(t) = -16t2 + (V0 sin A)t + h0
- 16t2 + (90 sin 30)t + 7
- 16t2 + 45t + 7 <- (quadratic)
1. When is the ball 25ft above ground?
h(t) = 25 → 25 = -16t2 + 45t + 7
0 = -16t2 + 45t - 18
- graph & find intersecting pts [h(t) = 25]
- quadratic formula
t = .5 sec and 2.3 sec
direct variation
has the form f(x) = kxn
where n is a pos integer & k doesn’t equal 0
the exponent n is also **degree **of the function
direct variation problems
solve for k to write a function
ball bearing varies directly w/ cube of radius, r = .4cm and w = 2.1g
write direct var function that describes weight in terms of radius
r = radius W(r) = weight
W(r) = kr3
2.1 = k(.4)3
k = 32.8
W(r) = 32.8r3
polynomial function
sum of 1+ direct variation functions
Ex: P(x) = x4 + 16x3 + 5x2 - 13x + 6
zeros of a function
values of x that make f(x) = 0
radical problems
sqrt(x + 7) - 1 = x
sqrt(x + 7) = x + 1
(sqrt[x+y])2 = (x+1)2
x + 7 = (x+1)(x+1)
x + 7 = x2 + 2x + 1
0 = x2+ x - 6
x = -3, x = 2
**check for extraneous **
x = 2
radical functions
functions that have a variable under a radical symbol
f(x) = √x + b → pos up, neg down
f(x) = √(x-c) → neg right, pos left
f(x) = a√x → 0 < a < 1 steeper, a > 1 less steep
f(x) = -√x → reflection
Properties of Radicals
n√b = x when xn = b
n√(bn) = {b when n is odd} { |b| when n is even}
n√(ab) = n√a • n√b {when n is odd, for all values of a & b; when n is even, for pos. values of a & b}
rational function
a function defined by a rational expression
rational expression
a quotient of 2 polynomials
graphing: find asymptotes
rational function problems
Eric took 2 exams & average was 63%. if gets 100 on rest of exams, how many does he need to take for aver 85%?
t = # of tests
(63 • 2 + 100t) / (t + 2) = 85
126 + 100t = 85(t + 2)
126 + 100t = 85t + 170
15t = 44
t = 2.93 → 3 exams
composite of 2 functions
the composite of 2 functions f and g = the function f(g(x)), which is read “f of g of x”
u write (f○g)(x), which is read “the composite of f and g”
to find (f○g)(x), u can find g(x) first and then find f(x) for that value
compositing problems
Given h(x) = x2 + x and k(x) = 6x, find
- (h○k)(x)
h(k(x) = h(6x) <- substitute in
h(x) = x2 + x → h(6x) = (6x)2 + (6x) = 36x2 + 6x
- (h○k)(1/3)
just use previous rule to plug in
4 + 2 = 6
-
OPERATIONS ⇒ Given: f(x) = x2 + 1 and g(x) = x2 - 1
- f(x) + g(x) = (x2 + 1) + (x2 - 1) = 2x2
- f(x) - g(x) = (x2 + 1) - (x2 - 1) = (x2 + 1) + (-x2 + 1) ← flip the signs when subtracting = 2
- f(x) ÷ g(x) = (x2 + 1)(x2 - 1) = x4 - 1 ← (x² + 1) / (x² - 1)
only simplify if neg, √, or fraction in denom
- word problems - Chris pays 15% of quarterly earnings for tax and adds $50 to be on the safe side. earns $90 a day. days(d). x = payment on “x” dollars. find function for amount earned as function of days
e(d) = 90d ← income
E(x) = 0.15x + 50 ← tax
for d days, estimated tax payment = (E ○ e)(d) = E(90d)
E(0.15x + 50) → E(90d) = 0.15(90d) + 50 = 13.5d + 50
synthetic proof
proof built using a system of postulates & theorems in which the prop’s of figures, but not their actual measurements r studied
justifications of synthetic proof
given statements
definitions
postulates
previously proved theorems
Bisecting Diagonals Th
if the 2 diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram
implications
if-then statements that can be represented by symbols
Ex: p → q reads “If p, then q”
logically equivalent
either both true or both false
original & contrapositive
not logically equivalent
just cuz original = true, doesn’t mean converse & inverse r too
converse
q → p
If q, then p
inverse
~p → ~q
If not p, then not q
contrapositive
~q → ~p
If not q, then not p
median (of a triangle)
a segment joining a vertex to the midpt of the opp. side
coordinate proof
a proof based on a coord. system in which all pts r represented by ordered pairs of #’s
justifications for coordinate proof
distance & midpt formulas
parallel lines have the same slope
perp. lines have slopes that r neg. reciprocals of each other
a geometric figure may be placed anywhere in the coord. plane
distance formula
midpoint formula
Isosceles Median Theorem
In an isosceles triangle, the medians drawn to the legs r equal in measure
isosceles trapezoid
a trapezoid w/ a line of symmetry that passes through the midpts of the bases
Isosceles Trapezoid Th
in an isosceles trapezoid
- the legs r equal in measure
- the diagonals r equal in measure
- the 2 angles@ each base r equal in measure
inclusive definition
a definition that includes all possibilites
exclusive definition
a definition that excludes some possibilities
quadrilateral chart
past postulates & theorems
Addition, Subtraction, Mult, Div Prop’s of Eq Post’s
Reflexive Prop of Eq Post
Subsitution
Distributive
If 2 angles r supp’s of same angle, then r equal in measure
if 2 angles r compl’s of same angle, then equal
Straight Angle Post - if the sides of an angle form a straight line, then the angle is a straight angle w/ measure 180º
Angle/Segment Addition Post - for any seg/angle, the measure of the whole = to the sum of the measures of its non-overlapping parts
vertical angles r =
the sum of the measures of the angles of a triangle = 180º
an exterior angle of a triangle = the sum of the measures of its 2 remote interior angles
if 2 sides of a triangle r =, then the angles opp those sides r =, and vice versa
if a tri is equilateral, then also equiangular, w/ three 60º angles, and vice versa
if 2 parallel lines r intersected by a trans, then corr angles r =, vv
if 2 parallel lines r intersected by a trans, then alt int angles r =, vv
if 2 par lines r inters’d by a trans, then co-int angles r supp, vv
if 2 lines r perp to the same trans, then they’re parallel
if a trans = perp to one of 2 par lines, then its perp to the other one as well
thru a pt not on a given line, there’s 1 and only 1 parallel line to the given line
if a pt is the same distance from both endpts of a segment, then it lies on the perp bisector of the seg
a seg can be drawn perp to a given line from a pt not on the line
AA similiarity - if 2 angles of 1 tri r = to 2 angles of another tri, then the 2 tri’s r similar
if a line is drawn from a pt on 1 side of a tri parallel to another side, then it forms a tri similar to the original tri
in a tri, a seg that connects the midpts of 2 sides is parallel to the 3rd side & half as long
ASA, AAS th’s
SAS, SSS post’s
If the alt = drawn to the hyp of a right tri, then the 2 tri’s formed r similar to the orginal tri & to each other
Pythagorean Th
if the alt is drawn to the hyp of a right tri, then the measure of the alt is the geometric mean b/w the measures of the parts of the hyp
the sum of the lengths of any 2 sides of a tri > length of 3rd side
in an isosc tri, the medians drawn to the legs r equal in measure
in a parallelogram, the diagonals have the same midpt
in a rectangle, the diagonals r equal in measure
in a kite, the diagonals r perp to each other
in a parallelogram, opp sides r equal in measure
if a quadrilateral is a parallelogram, then consecutive angels r supp
if a quad is parallelogram, then opp angles r =
the sum of the measures of the angles of a quad = 360º
if both pairs of opp angles of a quad r equal in measure, then the quad = a parallelogram
Interior Angle Measures in Polygons Th
the sum of the angle measures of an n-gon is given by the formula
S(n) = (n - 2)180º
Exterior Angle Measures in Polygons Th
the sum of the exterior angle measures of an n-gon, 1 angle at each vertex, is 360º
regular polygon
iff all its sides & angles r = in measure
inscribed
drawn inside the figure
circumscribed
drawn outside the figure
chords
segments whose endpts r on the circle
perp bisector of a chord th
the perp bisector of a chord of a circle passes thru the center of the circle
central angle
an angle w/ its vertex @ the center of the circle
measure of an arc intercepted (cut off) by a central angle = measure of that central angle
minor arc
< 180
can be named w/ 2/3 letter (just remember that a major arc is named w/ 3 letters to distinguish it from a minor arc w/ the same endpts)
semicircle
= 180
named w/ 3 letters
outside letters = diameter
major arc
180 < arc < 360
named w/ 3 letters
inscribed angle
an angle formed by 2 chords that intersect at a point ON circle
intercepted arc
the arc that lies w/in an inscribed angle
inscribed angle measure th
the measure of an inscribed angle of a circle = 1/2 the measure of its intercepted arc
inscribed right angle th
an inscribed angle whose intercepted arc is a semicircle is a right angle
equal inscribed angles th
if 2 inscribed angles in the same circle intercept the same arc, then they r = in measure
intersecting chords theorem
the measure of angle formed by 2 chords that intersect INSIDE a circle = 1/2 the sum of the measures of the intercepted arcs
.5(a + b)
secants & tangents th
the measure of an angle formed by 2 secants, 2 tangents, or a secant & a tangent drawn from a pt outside the circle = 1/2 the difference of the measures of the intercepted arcs
½(big - small)
tips for finding angles
continue radius to diameter
use systems of equations
remember perp rule
tangent
a line in the plane of a cricle and intersecting the circle in exactly 1 pt
secant
a line intersecting the circle in 2 pts
Short Point Post
a seg can be drawn perp to a given line from a pt not on the line
the length of this seg is the shortest distance from the pt to the line
Perp Tangent Th
if a line is tangent to a circle, then the line is perp to the radius drawn from the center to the pt of tangency
Converse of Perp Tangent Th
if a line in the plane of a circle is perp to a radius at its center endpt, then then the line is tangent to the circle
Equal Tangents Th
if 2 tangent segments are drawn from the same pt to the same circle, then they equal in measure
semiperimeter
half the perimeter
how to find area of circumscribed polygons using trig
- total degrees = 360º
- divide 360 by # of vertices to find all internal angles
- divide internal angles by 2 to find angle in new right triangle
- use trig to find sides (already have radius & angle & know its right tri)
- find area of original triangle
- multiply by # of vertices
Ex: pentagon w/ radius 30cm
- total degrees = 360
- 360÷5 = 72
- 72÷2 = 36
- tan36º = x/30; x = ~21.8
- 21.8 • 2 = 43.6; ½bh = ½(30)(43.6) = 654cm²
- 654 • 5 = 3,270cm3
area of a circumscribed polygon
the area of any circumscribed polygon is the product of the radius(r) of the inscribed circle & the semiperimeter(s)
A = rs
polyhedron
a space figure whose faces are all polygons
semiregular polyhedron
a polyhedron w/ faces that r all regular polygons, & w/ the same # of faces of each type @ each vertex
regular polyhedron
a polyhedron w/ faces that r all the same type of regular polygon, & w/ the same # of faces @ each vertex
5 regulars: tetrahedron, hexahedron, octahedron, dodecahedron, icosahedron
tetrahedron
4 equilateral triangles
hexahedron
6 squares
octahedron
8 equilateral triangles
dodecahedron
12 regular pentagons
icosahedron
20 equilateral triangles
Convex Polyhedron Postulate
in any convex polyhedron, the sum of the measures of the angles at each vertex is less than 360º
net
a 2D drawing showing the connected faces of a space figure & how they r connected
can be cut out & “folded up” to form the space figure
defect
the angle measure of the gap @ a vertex on a net for a polyhedron
can be found by subtracting the sum of the angles @ that vertex from 360
Euler’s formula
F + V = E + 2
f = # of faces
v = # of vertices
e = # of edges
formulas to know
explicit arithmetic → an = a1 + d(n - 1)
recursive arithmetic → a1 = first term; an = an-1 + d
explicit geometric → an = a1rn-1
recursive geometric → a1 = first term; an = (an-1)r
sum finite arithmetic series → S = n(a1+an) ÷ 2
sum finite geometric series → S = a1 - anr ÷ 1-r
sum geoemtric infinite series → S = a1 ÷ 1-r; |r| < 1
sequence
an ordered list of numbers
terms
the numbers in a sequence
finite sequence
a sequence with a last term
infinite sequence
a sequence with no last term
graphing sequences
each term is paired w/ a number that gives its position in the sequence
by plotting pts with coord’s (position, term), u can graph a sequence on a coord plane
limit of a sequence
when the terms of an infinite sequence get closer and closer to a single fixed number L, then L is called the limit
not all infinite sequences have one; repeating ones, for ex, like 1, 2, 3, 1, 2, 3, …
graphing it often helps
explicit formula
gives the value of any term an in terms of n
finding explicit formulas
Ex: Given 90, 83, 76, 69,…, find a formula for the sequence
- Find a pattern. || a repeated subtraction of 7
- write the 1st few terms. Show how u found each term. ||
a1 = 90
a2 = 83 = 90 - 1(7)
a3 = 76 = 90 - 2(7)
a4 = 69 = 90 - 3(7)
- Express the pattern in terms of n. || an = 90 - (n - 1)7
2.
subscript 0
when the 1st term of a sequence represents a starting value before any change occurs, subscript 0 is often used
Ex: monthly bank account balances, 1st term is v0 for initial deposit. next term = v1, for 1st month’s interest, etc. etc.
percentage explicit formulas
Ex: bacteria count increases 10% each day; 10,000 now; Find formula for bacteria count after n days
- d + .1d {if annual interest, compounded monthly, then d + (.1/12)d}
d(1 + .1)
d(1.1)
- d0 = 10,000
d1 = 10,000(1.1)
d2 = d1(1.1)
= 10,000(1.1)(1.1)
= 10,000(1.1)²
d3 = d2(1.1)
= 10,000(1.1)2(1.1)
= 10,000(1.1)3
•
•
•
dn = 10,000(1.1)n
self-similarity
the appearance of any part is similar to the whole shebang
recursive formula
tells how to find the nth term from the term(s) before it
2 parts:
- a1 = 1 ↔ value(s) of 1st term(s) given
- an = 2an-1 ↔ recursion equation
finding recursive formulas
Ex: 1, 2, 6, 24
- Write several terms of the sequence using subscripts. Then look for the relationship b/w each term & the term before it.
a1 = 1
a2 = 2 = 2 • 1
a3 = 6 = 3 • 2
a4 = 24 = 4 • 6
- Write in terms of a
a2 = 2 • a1
a3 = 3 • a2
a4= 4 • a3
- Write a recursion equation
an = nan-1
- Write recursive formula
a1 = 1
an = nan-1
percentage recursive formulas
Ex: 650mg of aspirin every 6h; only 26% of aspirin remaining in body by the time of new dose; what happens to amount of aspirin in body if taken several days?
- write a recursion equation
amount aspiring after nth dose = 26% amount after prev. dose + new dose of 650mg
an = (0.26)(an-1) + 650
- Use a calc
Enter a1 → 650
Enter recursion equation using ANS for an-1 → .26ANS + 650
Keep pressing Enter
sequence appears to approach limit of about 878
arithmetic sequence
a sequence in which the diff b/w any term & the term before it = a constant
Ex: 2,4, 6, 8
+2, +2, +2
common difference
d
the constant value an- an-1
geometric sequence
a sequence in which the ratio of any term to the term before it is a constant
Ex: 2, 4, 8, 16
x2, x2, x2`
common ratio
r
the constant value an / an-1
explicit arithmetic formula
an = a1 + (n - 1)d
recursive arithmetic formula
a1 = first term
an = an-1 + d
using explicit formulas to find out how many terms r in a finite sequence
Ex: 33, 29, 25, 21,…, 1
- arithmetic, geo, or neither?
d = -4 → arithmetic
- Use a formula
an = a1 + (n - 1)d
1 = 33 + (n - 1)(-4)
1 = 33 - 4n + 4
-36 = -4n
n = 9
there r 9 terms
explicit geometric formula
an = a1rn-1
recursive geometric formula
a1 = first term
an = (an-1)r
geometric mean
√(ab)
Ex: find x in geo sequence 3, x, 18
- In geo sequence, an/aan-1 is a constant
a2/a1 = a3/a2
x/3 = 18/x
x2 = 54
x = + √54 = _+_3√6
x is 3√6 or -3√6
series
the indicated sum of the terms when the terms of a sequence are added
sequence = 1, 2, 3, 4, 5, 6
series = 1 + 2 + 3 + 4 + 5 + 6
finite series
has a last term
infinite series
has no last term
arithmetic series
its terms form an arithmetic sequence
sum finite arithmetic series
S =
n(a1 + an)
________
2
finding the sum of a finite arithmetic series
Ex: 7 + 12 + 17 + 22 +…+ 52
- arith, geo, or neither
d = 5, arithmetic
- find the # of terms
an = a1 + (n - 1)d
52 = 7 + (n - 1)5
52 = 7 + 5n - 5
n = 10 → 10 terms
- Use formula → S = 295
sigma notation
uses summation symnbol Greek sigma Σ
Read: the sum of 2n for integer values of n from 1 to 6
if infinite series, number on top is ∞
expanded form
when u substitute the values of n into the formula
geometric series
its terms from a geometric sequence
sum finite geometric series
S =
a1 - anr
________
1 - r
evaluating sigma notation
if finite,
- write in expanded form
- decide if arithmetic, geo, or neither
- use formula for sum of whatever type it is
if infinite,
- see whether a sum even exists first by expanding first few terms
- if geometric, use ratio to see if sum exists. if arith, graph.
- find sum using formula or graphing
partial sum
the sum of the first n terms of an infinite series
sequence of partial sums
2, (2+4), (2+4+6), … forms a sequence of partial sums for the infinite series 2 + 4 + 6 +…
sum of an infinite series
if the sequence of the partial sums of an infinite series has a limit, then that limit is the sum of the series
finding sums of infinite series by graphing
Ex: 3 + (-1.5) + .75 + (-0.375) + …
- Find common ratio → r = 0.5
- Find 1st few partial sums
S1 = 3
S2 = 3 + (-1.5) = 1.5
S3 = 1.5 + 0.75 + (-0.375) = 1.875
S5 = 1.875 + .1875 = 2.0625
S6 = 2.0625 + (-0.09375) = 1.96875
- graph the partial sums (position, term)
- limit is about 2, so sum is about 2
sum infinite geometric series
S = a1 / 1-r for |r| < 1
discrete exponential growth
represented by points
Ex: most species only produce once a year
continuous exponential growth
represented by a line, curve, etc.
Ex: over-lapping generations. some species bred thruout the year
exponential function
y = abx
y - amount after x period
a - initial value
b - growth factor
x - time period
how to write exponential functions and predict
2.9 mill ppl in 1980, increasing 1.7% each yr
- write an exponential function
- when will pop reach 4.5 mill?
a.
1. find growth factor b
pop @ end of yr = 100% of pop @ start + 1.7% of pop @ start
pop @ end of yr = 101.7% pop @ start of year
b = 1.017
- y = abx
y = (2.9)(1.017)x
b.
- Use a graph
- Graph the equation y = (2.9)(1.017)x
- x-value of 0 = 1980, x-value of 26 = 2006
- Use recursion
- Enter initial amount 2.9 & repeatedly multiply by growth factor (1.017)
- count # of times pressed Enter (26)
- 1980 + 26 = 2006
exponential growthx
b > 1
y = ab
b > 1
exponential decay
y = abx
0 < b < 1
negative exponents
b
b-x = (1/b)x
Ex: y = 52(6/5)-x = 52(5/4)x
half-life problems
1200 ppl; every ½ hour, ½ ppl leave
1st half-life → (1200)(½)
2nd half-life → (1200)(½)(½)
f(x) = 1200(½)x
**or **just use formula
how many ppl after 3 hours
about 18
fractional exponent rules
a1/n = ⁿ√a
am/n =(ⁿ√a)m or ⁿ√(am)
IF n IS EVEN, MUST USE ABSOLUTE VALUE
solving exponent algebraic equations
find the value of b when f(x) = 4bx and f(¾) = 32
4b¾ = 32
b¾ = 8
b¾(4/3)= 84/3
b = 84/3 = (3√8)4 = 24 = 16
e
the number e is an irrational # that is approx. 2.718 ← this is also the limit of the sequence (1 + 1/1)1, (1+½)2, (1+1/3)3, …
logistic growth function
a function in which the rate of growth of a quantity slows down after initial increasing/decreasing exponentially
solving e problems
spread of flu in 1,000 ppl modeled by y = 1000/(1 + 990e-0.7x), where y = the # of ppl after x days
- how many ppl after 9 days?
Graph the equation
read y when x = 9 → abt 355 ppl
- horizontal asymptotes?
trace along same graph
min. y-value gets close to but never reaches 0
max. y-value gets close to but never reaches 1000
y = 0, y = 1000
- estimate max # of ppl → max. of y = 1000ppl
investment formulas
A = P(1 + r/n)nt
A = Pert (for continuous)
P - initial value
r - rate (without 1)
n - # of time a year
t - years
inverse functions
two functions f & g are inverse functions if g(b) = a whenever f(a) = b
graph = reflection of the graph of the original function over the line y = x
inverse of f(x) can be written f-1(x) or f-1
graphing inverse functions
a. y = 2x
b. y = x2
1. plot the points to grpah each function. then interchange the coordinates of the original points and plot these points
deciding existence of inverse functions
an inverse is a function. if a reflection of a function over the line y = x isn’t a function, then the inverse doesn’t exist
a. y = 2x b. y = x2
1. Use the vertical line test to decide whether a reflection is the graph of a function (inverse)
- or-
2. Just like vertical line tests, u can use the horizontal line test to see whether a function has an inverse (original)
writing inverse equations
interchange x & y, and solve for y
logarithmic function
the inverse of the exponential function f(x) = bx and written as f-1= logbx
x = ba ↔ a = logbx
x on outside, b in middle, a in center
base of a log can be any pos. # except 1
log4(-2) is undefined! can’t have neg log
common logarithm
a log w/ base 10
common log of x written as log x
x = 10a ↔ a = log x
natural logarithm
a log w/ base e
usually written as ln x
x = ea ↔ a = ln x
evaluating logs
evaluate each. (Find a).
- log464
log464 = log443 → a = 3; has to be 43 cuz base = 4
- log(1/10,000)
log(1/10,000) = log10-4 → a = -4
- ln5.3 → use calc
- log145 → use calc
solving logs
when solving these, remember that x isn’t necessarily the x in the formula. it can be a, b, or x
solve logx81 = 2
logb81 = 2
b2 = 81
b = 9
Solve. round decimal answers to nearest hundredth
a. 10x = 15
10a = 15
a = log 15 = abt 1.18
b. ea = 29
ea = 29
a = ln 29 = abt 3.37
c. log2x + log2(x-2) = 3
log2x + log2(x-2) = 3
log2x(x-2) = 3
x(x-2) = 23
x2 - 2x = 8
x2 - 2x - 8 = 0
(x+2)(x-4) = 0
x + 2 = 0 or x - 4 = 0
x = -2 x = 4
check for extraneous solutions! Sub possible solutions into the original equation to be sure they’re not extraneous
x = -2 is undefined, cuz no neg logs log2(-2)
properties of logs
M, N, and P are pos. #’s w/ b not equaling 1, and k is any real #
Product of Logarithms Property
logbMN = logbM + logbN
Quotient of Logarithms Property
logbM/N = logbM - logbN
Power of Logarithms Property
logbMk = k logb M
writing in terms of logM and logN
a. logM2N3
logM2 + logN3 = 2logM + 3logN
b. log3√(M)/N4
log3√M - logN4 = logM1/3 - logN4 = 1/3logM - 4logN
simplifying logs
ln18 - 2ln3 + ln4
ln18 - ln32 + ln4 → power prop.
ln18 - ln9 + ln4
ln18/9 + ln4 → quotient prop.
ln2 + ln4
ln(2•4) → product prop.
ln8
log and exp word problems
- L = 10log(I/I0) What is the change in loudness(L) when I is doubled?
L1 = original loudness L2 = loudness after intensity is doubled
increase in loudness = L2 - L1
L2 - L1 = 10log(2I/I0) - 10log(I/I0)
10log(2•I/I0) - 10log(I/I0)
10(log2 + logI/I0) - 10log(I/I0)
10log2 + 10log(I/I0) - 10log(I/I0)
10log2 = abt 3
- A(t) = A0(0.883)t with A(t) - amount present t thousand yrs after death, A0 - amount @ time of death, and t - amount time since death (in 1000’s of yrs)
found in 1968, died 8000 yrs ago, 37% present now; estimate age of the bone
A0(0.883)t = A(t)
A0(0.883)t = 0.37A0
0.883t = 0.37
log(0.883)t = log0.37
t log 0.883 = log0.37
t = log0.37/log0.883
t = 8
Change of Base Property of Logs
for all pos. #’s with b and c not equaling 1,
logbM = (logcM) / (logcb)
REMEMBER
when evaluating sigmas, or whatever, if it’s something like (3/4)k, then know that 3/4 is the common ratio! or if 7(-2)c, -2 is common ratio!
when calculating exponents with negative bases, be sure to use parenthesis! (-.75)3
