FP3 Vectors

Question 1

Distance of point to line equation

(Point: c, Line: a + λb)

Answer 1

Question 2

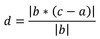
Distance between parallel lines equation

(Points on lines: a₁/a_2, Direction Vector: b)

Answer 2

Question 3

Distance between skew lines equation

(Points on lines: a₁/a₂, Direction Vectors: b₁/b₂)

Answer 3

Question 4

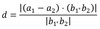
How to work out the angle between two planes

Answer 4

Use scalar product to find the angle between the normals (therefore a= n₁, b=n₂)

Question 5

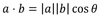
How to work out the angle between a line and a plane

Answer 5

Use the scalar product to find the angle between the line’s direction and the plane’s normal, and subtract this value from 90°

Question 6

How to work out line of intersection of 2 planes

Answer 6

The direction vector of the line of intersection is perpendicular to both plane’s normals, therefore:

n₁ x n₂ = b

Then use simputaneous equations to find a point on both planes and this will be a, for line equation in form:

r = a + λb

Question 7

Distance of point to plane

(Plane equation in form: r.n=d where n is the normal, r is a general point. Position of point: a)

Answer 7

Use equation: Distance=

Question 8

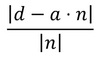
Area of triange

Answer 8

Question 9

Area of Parallelogram

Answer 9

Question 10

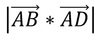
Volume of Parallelepiped

Answer 10

Where a and b represent vector sides of the parallelogram at the base and c represets the vector upwards in the 3rd dimension:

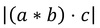
Note: a.(bxc) = b.(cxa)

Question 11

Volume of Tetrahedron

Answer 11

Same term definitions as volume of parallelepiped

Question 12

Vector cross product formula

Answer 12

Where n stands for a unit vector perpendicular to both a and b. (in the direction that a right handed screw would move when turned a -> b)

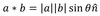
Note: b x a = -a x b, and to find a unit vector, divide the vector by it’s magnitude.

Question 13

What is an alternate equation for a straight line in vector form?

Answer 13

(r-a) x b= 0

Can also be written as rxa - axb = 0 and hence as

rxa=axb)

Question 14

What are the different forms for the eqaution of a plane?

Answer 14

r.n=a.n (r.n=d)

(which can be converted to catesian form by inputting r= xi+yj+zk)

r= a + λb + μc

Where a is the position vector of a point in the plane, b and c are non-parallel vectors in the plane and r in the position vector a general point on the plane.

Question 15

How to find the point of intersection of a line and a plane.

Answer 15

Enter the line in column matrix form and substitute for r in the plane’s eqation, r.n=a.n .