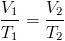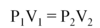Gases, Liquids, and Solids

Question 1

Define and give the three examples of:

a phase

Answer 1

A phase is a physically distinct form of a substance that can be separated from another form. Generally phase is used interchangeably with “state of matter”.

Solid, liquid, and gas are the three phases of matter that most chemistry courses, as well as the AP Chemistry exam, will test.

Question 2

Which two state functions can be used to actively change the phase of a substance?

Answer 2

Temperature (Heat, Enthalpy) can be added or removed. In general, an increase in temperature drives the phase change solid⇒liquid⇒gas.

Pressure (Volume) can be added or removed. In general, an increase in Pressure (or decrease in Volume) drives the phase change gas⇒liquid⇒solid.

Question 3

What name is associated with a phase change from

1. solid to liquid?
2. liquid to solid?

Answer 3

1. solid⇒liquid is fusion (melting)
2. liquid⇒solid is freezing (solidification)

Question 4

What name is associated with a phase change from

1. gas to liquid?
2. liquid to gas?

Answer 4

1. gas⇒liquid is condensation
2. liquid⇒gas is vaporization (boiling)

Question 5

What name is associated with a phase change from

1. gas to solid?
2. solid to gas?

Answer 5

1. gas⇒solid is deposition
2. solid⇒gas is sublimation

Question 6

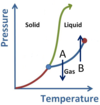
What phase is the substance in sections A, B, and C in the below diagram?

Answer 6

• A represents the Solid phase region.
• B represents the Liquid phase region.
• C represents the Gas phase region.

Question 7

What phase conversions are being shown with arrows A and B?

Answer 7

• A is Fusion (or Melting)
• B is Freezing (or Solidification)

Question 8

What phase conversions are being shown with arrows A and B?

Answer 8

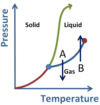
• A is Vaporization (or boiling)
• B is Condensation

Question 9

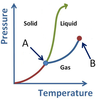
What phase conversions are being shown with arrows A and B?

Answer 9

• A is Sublimation
• B is Deposition

Question 10

What points are arrows A and B pointing to?

Answer 10

• A is the Triple Point.
• B is the Critical Point.

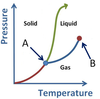
Note: though the concept of Plasma exists, the AP Chem exam does not explicitly test this as a phase.

Question 11

Explain the significance of the critical point.

Answer 11

The critical temperature and critical pressure combine to be the critical point:

• the critical temperature is the temperature above which a distinct liquid-to-gas vaporization can no longer be accurately determined.
• the critical pressure is the pressure above which a distinct gas-to-liquid condensation can no longer be accurately determined.

Question 12

Explain the significance of the triple point.

Answer 12

The triple point is the point at which a substance can exist in equilibrium in all three states (solid, liquid, and gas).

This means that instantaneously, a substance at its triple point can interconvert between any phase.
Ex: water at its triple point would exist as ice, liquid water, and steam - all at one temperature and pressure.

Question 13

How does the phase diagram of water differ from the one below?

Answer 13

Water has a slightly negative sloped Solid/Liquid boundary.

This is due to water’s Solid phase being less dense than its Liquid phase.

Question 14

Different materials require different applications of heat in order to transition into a new phase. Why is this?

Answer 14

The difference is due to intermolecular forces.

The attraction of molecules to each other determines at which temperature mixtures will have phase changes, and subsequently the amount of heat necessary to make that transition.

Question 15

What types of intermolecular forces exist?

Answer 15

From strongest (1) to weakest (4), they are:

1. Ionic Forces
2. Hydrogen Bonds
3. Dipole-Dipole
4. London Dispersion Forces

Question 16

Define:

dipole forces

Answer 16

Dipole forces occur when a molecule with polar bonds has the geometry to become overall polar. This results in partially positive and negative charges, and these opposite charges attract other charged molecules in the mixture.

Question 17

Define:

hydrogen bonds

Answer 17

Hydrogen bonds are a product of H being covalently bonded to either O, N, or F. This is an extreme form of the dipole-dipole force.

The high electronegativity difference between these atoms and hydrogen creates strong dipoles, which consequently result in the strongest dipole-dipole interactions between molecules.

Question 18

Define:

London Dispersion forces

Answer 18

Dispersion forces (also called Van der Waals forces) are an instantaneous polarization of molecules that would otherwise be non-polar.

This process is also referred to as an induced dipole because there is an instantaneous reorganization of the electron cloud leading to partial polarization. The more valence electrons present in either a molecule or in a mixture, the more possible repulsion of electron clouds, and the more induced dipoles.

Question 19

Define:

ionic forces

Answer 19

Ionic forces occur when two oppositely charged ions (cations and anions) attract each other.

In general, ions attract to a polar molecule first, then attract each other - hence this is often called Ion-Dipole force. (Two Ions attracting each other would otherwise prefer to Ionic Bond, which is an intramolecular force, not an intermolecular force.)

Question 20

Describe how the boiling point of a substance changes depending on the strength of the intermolecular forces present?

Answer 20

The stronger the intermolecular forces present, the higher the boiling point. This is due to the molecules being more tightly attracted to each other is the liquid phase.

In order of highest (1) to lowest (4) boiling points:
Ionic Forces
Hydrogen Bonds
Dipole-Dipole
Dispersion Forces

Question 21

List forces from strongest to weakest:

Dipole-Dipole
Hydrogen Bonds
London Dispersion Forces
Ionic Forces

Answer 21

1. Ionic Forces
2. Hydrogen Bonds
3. Dipole-Dipole
4. London Dispersion Forces

Question 22

Define:

H_v

Answer 22

H_v is the heat of vaporization. It represents the energy necessary to convert a liquid to a gas.

Question 23

Define:

H_f

Answer 23

H_f stands for the heat of fusion. This is the amount of energy that is necessary to convert a solid to a liquid.

Question 24

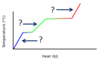
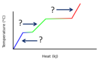
What processes are associated with the plateaus A and B, for the general heating curve below?

Answer 24

• At A, fusion is occurring.
  H_f is used to calculate the heat needed for plateau A.
• At B, vaporization is occurring.
  Hv is used to calculate the heat needed for plateau B.

Question 25

Why are the slopes zero for plateaus A and B?

Answer 25

Zero slope means no temperature change. This occurs at these times because any heat input is dedicated to breaking bonds between molecules, instead of increasing temperature.

Ex: during the vaporization of water, heat is needed to break the hydrogen bonds between liquid water molecules and convert it to gaseous steam.

Question 26

What equation determines the heat added in the sections where the temperature is rising in the below diagram?

Answer 26

q = mcΔT

This formula calculates heat required to raise a certain mass of a substance by a change in temperature ΔT.

where:
q = heat required in J
m = the sample’s mass in g
c = the substance’s specific heat in J/g*K
ΔT = temperature change in K

Question 27

What is the value of specific heat (c) for water?

Answer 27

Water’s specific heat is c = 1 cal/gºK.

In SI units, c ≈ 4.2 J/gºK.

Question 28

What is the equation to calculate heat required when at the plateaus in the phase change diagram below?

Answer 28

q = mH_L

This formula calculates heat required to change a certain mass of a substance from one phase to another. H_L would be H_f for the first plateau and H_v for the second plateau.

where:
q = heat required in J
m = mass in g
H_L = latent heat of phase change

Question 29

How much heat would be required to increase the temperature of 20g water by 5 degrees, starting at 20 ºC?

Answer 29

100 cal.

At 20 ºC, water is a liquid and has specific heat c = 1 cal/gºC.
Since temperature is changing and phase is not changing within the temperature range 20-25, use the formula q = mcΔT.
hence: q = 20(1)(5) = 100cal.

Question 30

Define:

Standard Temperature and Pressure (STP)

Answer 30

STP is 0º C and 1 atm

Chemistry exams occasionally refer to Standard Ambient Temperature and Pressure (SATP), which you should know is 25ºC and 1 atm.

Question 31

What are the assumptions of:

the kinetic molecular theory of gases

Answer 31

The kinetic molecular theory assumes an idealized version of gas, which makes calculating relationships easier. There are four assumptions:

1. A gas molecule has no volume (point molecule).
2. The collisions between gas molecules are completely elastic.
3. There are no dissipative forces due to collisions.
4. The average kinetic energy of gas molecules is directly proportional to the temperature of the gas.

Question 32

Give the relationship and equation for:

Charles’s Law

Answer 32

Charles’ Law states that the volume of a gas is directly proportional to temperature while at a constant pressure.

Equation:

Question 33

If the pressure of an ideal gas system is held constant but the temperature is doubled, what does Charles’s Law predict will happen to the volume?

Answer 33

The system’s volume will double also.

Charles’s Law indicates that at a constant pressure, the temperature and volume of a gas are directly proportional.

Question 34

Give the relationship and equation for:

Boyle’s Law

Answer 34

Boyle’s Law states that the volume of a gas is inversely proportional to its pressure while at a constant temperature.

Equation:

Question 35

If the temperature of an ideal gas system is held constant but the pressure is reduced by 1/2, what does Boyle’s Law predict will happen to the volume?

Answer 35

The system’s volume will double.

Boyle’s Law indicates that at a constant temperature, the pressure and volume of a gas are inversely proportional.

Question 36

Give the relationship and equation for:

Avogadro’s Law

Answer 36

Avogadro’s Law states that the volume of a gas is directly proportional to the number of moles at a constant temperature and pressure.

V / n = k

where:
V = volume in L
n = number of moles
k = proportionality constant of the specific gas

Question 37

If the pressure and temperature of an ideal gas system are held constant but the number of moles is reduced to 1/3 of the original value, what does Avogadro’s Law predict will happen to the system’s volume?

Answer 37

The system’s volume will decrease to 1/3 also.

Avogadro’s Law indicates that at a constant pressure and temperature, the number of moles and volume of a gas are directly proportional.

Question 38

Give the equation for:

the Ideal Gas Law

Answer 38

The Ideal Gas Law combines Charles’, Boyle’s, and Avogadro’s Laws into one:

PV = nRT

where:
P = Pressure in atm or Pa
V = Volume in L
n = Number of moles
R = Ideal gas constant .082 L(atm)/mol(K) or 8.31 J/mol(K)
T = Temperature in K

Question 39

What is the volume of 1 mole of gas molecules at STP?

Answer 39

At STP, one mole of gas has a volume of 22.4 L

This is called the standard molar volume, and is true for a mole of any ideal gas at STP.

This value can be calculated using the Ideal Gas Law, but is worth memorizing.

Question 40

Give the equation for:

calculating the partial pressure of a gas in a mixture

Answer 40

P_A = x_AP_total

where:
P_A = pressure from gas A
x_A = mole fraction of A (moles of A divided by total moles of gas)
P_total = total pressure of the sytem from all moles of gas

Question 41

Give the equation for:

Dalton’s Law

Answer 41

P_total = P_A + P_B + P_C + …

Dalton’s Law states that the total pressure of a system of ideal gases can be thought of as the sum of all of the partial pressures that each gas exerts.

Question 42

Give the equation:

for internal energy (average kinetic energy) of a gas

Answer 42

U = KE_avg = (3/2)nRT

where:
U = potential internal energy in J
KE_avg = average kinetic energy in J
n = number of moles of gas
R = Ideal gas constant .082 L(atm)/mol(K) or 8.31 J/mol(K)
T = Temperature in K

Question 43

When does a gas deviate from its ideal state?

Answer 43

Gases deviate from ideal at:

1. Low temperatures
2. High pressures ( or very low volume)

Question 44

Why does low temperature and high pressure cause a gas deviate from its ideal state?

Answer 44

Gases deviate from ideal at low temperatures, because the molecules have very low kinetic energy (hence low velocity) and will start to attract based on the intermolecular forces.

Gases deviate from ideal at high pressures or very low volumes, because the molecules have very little actual space to move in and will start to exhibit characteristics more like a fluid than a gas.

Question 45

Give the equation:

Van Der Waals Equation

Answer 45

(P + a(n/V)²)(V - nb) = nRT

where:
P = Pressure in atm or Pa
V = Volume in L
n = number of moles
R = Ideal gas constant .082 L(atm)/mol(K) or 8.31 J/mol(K)
T = Temperature in K
a = attraction between molecules due to intermolecular forces
b = actual volume taken up by gas molecules

Note: the van der Waals equation predicts the behavior of non-ideal gases, taking into account the intermolecular attractive forces of the gas molecules and the space taken up by the non-point molecules.

Question 46

Explain whether a polar or nonpolar real gas will deviate more from ideal?

Answer 46

Polar gases will deviate more from ideal.

(P + a(n/V)²)(V - nb) = nRT

Remember: ‘a’ is the attractiveness between molecules. When ‘a’ is big (polar=attractive) the pressure term will be larger. Effectively, the gas will experience more pressure holding it together than the ideal gas law predicts.

Question 47

Explain whether a small or large molecule size real gas will deviate more from ideal?

Answer 47

Larger molecule gases will deviate more from ideal.

(P + a(n/V)²)(V - nb) = nRT

Remember: ‘b’ is the bigness of the actual molecules. When ‘b’ is big (larger size=big) the volume term will be smaller. Effectively, the gas will have less space to move in than the ideal gas law predicts.

Question 48

Define:

absolute temperature

Answer 48

The absolute temperature is any temperature that is given in Kelvin (K).

0 K is the temperature at which all molecules are assumed to cease moving completely. To convert Kelvin to Celcius:

K = C + 273.15