Gütekriterien für Schätzfunktionen

Question 1

Erwartungswert, Varianz, Standardabweichung, Warscheinlichkeitsverteilung von Schätzfunktionen

Answer 1

Da Schätzfunktionen Zufallsvariablen sind, haben sie eine Wahrscheinlichkeitsverteilung, einen Erwartungswert, eine Varianz, eine Standardabweichung.

→Anhand d. Erwartungswertes, d. Varianz und d. Standardabweichung von Schätzfunktionen lassen sich Gütekriterien für Schätzfunktionen formulieren.

(Aus der Beschreibung der Zufälligkeit der Schätzwerte mithilfe der Wahrscheinlichkeitstheorie ergeben sich Gütekriterien für die Punktschätzung)

Question 2

Gütekriterien für Schätzfunktionen

Answer 2

1. Erwartungstreue
2. Effizienz
3. Konsistenz

Question 3

Erwartungstreue

Answer 3

Eine Schätzfunktion ist erwartungstreu, falls die Schätzwerte bei unendlicher Wiederholung des Zufallsexperiments (Ziehung einer Zufallsstichprobe der Größe n) im Mittel dem wahren Parameterwert entsprechen.

Da die Schätzwerte Realisationen der Schätzfunktion sind, und der Mittelwert unendlich vieler Realisationen einer Zufallsvariable deren Erwartungswert ist, ergibt sich:

Question 4

Standardfehler von Schätzfunktionen

Answer 4

Streuungsmaß (Standardabweichung wird im Fall bei Schätzfunktionen Standardfehler genannt)

Je geringer der Standardfehler, desto weniger streuen die Schätzwerte (die meisten Schätzwerte liegen nahe an dem wahren Parameterwert) und desto genauer ist die Schätzfunktion (Erwartungstreue vorausgesetzt).

(Es gibt natürlich noch weitere Streuungsmaße)

Question 5

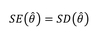
Effizienz

Answer 5

Eine Schätzfunktion ist effizient, falls sie erwartungstreu ist und einen geringeren Standardfehler als alle anderen erwartungstreuen Schätzfunktionen aufweist.

(Effiziente Schätzgunktion = „präziseste“ Schätzfunktion unter allen erwartungstreuen Schätzfunktionen)

Question 6

Konsistenz

Answer 6

Mit wachsendem Stichprobenumfang n sollte die Schätzfunktion immer “präziser” werden, d.h. der Standardfehler der Schätzfunktion immer kleiner werden und schließlich gegen Null gehen.