Lesson 1- Functions Flashcards
(40 cards)
What is a relation?

A set of ordered pairs.
Define: Domain
The set of first co-ordinates of a relation (R).
Define: Range
The set of second co-ordinates of a relation (R).
What are four ways to represent a relation?

Equation
Graph
Set of ordered pairs
Table of values
Determine the domain: (0,0) (1,1) (4,2) (9,3) (16,4)
0, 1, 4, 9, 16
Determine the domain and range of y = 2x + 1 .
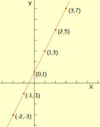
Domain: all real numbers
Range: all real numbers
When reading inequalities, we always read from the ___ to the ___.

Variable to the number
Read the following inequality: 7 <_ x
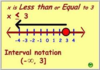
x is greater than, or equal to 7.
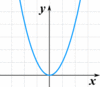
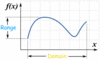
Determine the range of the following graph:
Range: -4 <_ y < 7
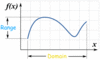
Determine the domain of the following graph:
Domain: -3 <_ x <_ 8
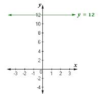
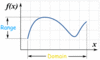
What is the domain of this graph?

Domain: -5 <_ x <_ 7
What is the range of this graph?

Range: (-3. -1, 1, 3)
What is the basic definition of a function?
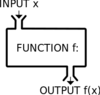
For every input value, there is only one output value.
Performs an operation on an input value and gives an output value.
What is the formal definition of a function?

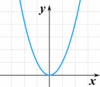
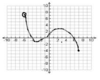
Does this graph represent a function?

No, the graph produces 2 y values for one x value.
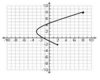
Does this graph represent a function?

No, the graph produces two y values for one x value.
How can we determine if an equation is a function?
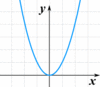
1- Solving for y to see if a unique y-value is produced.
2- Checking by substituting x- values (must produce only one y-value)
Is y^2 = x a function?
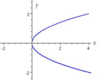
Is x^2 + y^2 = 16 a function ?
(hint: solve for y)
No, when solving for y:
y= +- /16 - x^2
A unique y-value is not produced.
Is this a function: (2,6) (3,9) (6,21) (8,43) ?

Yes, each x value produces a unique y-value.
Is x = /y a function?
Yes, when solving for y:
y = x^2
Is x2 = 9 - y2 a function?
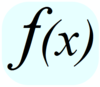
No, when solving for y:
y= +_ /9-x2
How do we determine the domain of a radical function?

Make the radicand greater than, or equal to 0.
How do we determine the domain of a rational function?

Make the denominator not equal to 0.