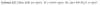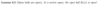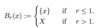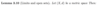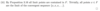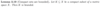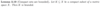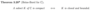Metric Spaces Flashcards by Hollie Pilkington

Q

Define a Metric Space.

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the formula for the Euclidean norm on ℝⁿ or ℂⁿ?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What are modulus and the Euclidean norm examples of?

A

Metrics

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the Euclidean norm on ℝ² called?

A

The dot product

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the formula for the Euclidean norm on ℂ²?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the formula for the Euclidean norm on ℝ²?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

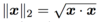
What is the formula for a Metric induced from inner products in vector spcaes?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

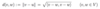
What inequality do you use to check the following metric satisfies the triangle inquality?

A

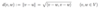
Cauchy-Schwarz

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

Define a norm.

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is a normed vector space?

A

A vector space equpped with a norm

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

Norms and inner products in vector spaces are examples of what?

A

Metrics

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the formula for the l_p-norm?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

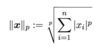
What is a name for the l_p-norm when p=1?

A

Taxicab norm

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the formula for the l_∞-norm?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is another name for the l_∞-norm?

A

Sup-norm.

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is another name for the Riemannian metric on ℂ?

A

Chordal metric on ℂ

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the Riemannian metric?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the Discrete metric

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the subspace metric?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is another name for the sunflower metric?

A

French railway metric

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the sunflower metric?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

Prove the following sunflower metric satisfies (D3) the triangle inequality.

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

What is the ‘jungle river’ metric?

A

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Q

Prove the following ‘jungle river’ metric is a metric.

A

Need to do - sheet 7

How well did you know this?

1

Not at all

2

3

4

5

Perfectly

Define **open and closed balls** in metric spaces.

Draw the unit balls for the l₁, l₂, l_∞. What does the l_p-norm look like in comparison?

What does collinear mean?

The points lie in a straight line

What two cases do you have to consider when drawing balls with respect to the sunflower metric?

1. Collinear 2. Not collinear

What do balls with respect to the sunflower metric look like?

Balls when x and y are not collinear and then straight lines where they are.

Define **open/closed** **sets in a metric space.**

What does clopen mean?

When a metric space is open and closed at the same time.

Give two common examples of clopen sets.

1. The empty set ∅ 2. The whole metric space X

What is a lemma about open balls?

Prove the following Lemma.

Are the following subets of the complex plane open or closed: ℍ, ⅅ, ℂ٭, B_r(z) and ℂ\ℝ_≤0?

Open

What is the generic formula for a ball with respect to the discrete metric space?

Are balls with respect to the discrete metric open or closed?

Clopen

Prove balls with respect to the discrete metric are clopen.

Give an example of a set which is neither open or closed?

[0,1)

When is a set clopen?

When the set and its complement are both open

What is the Lemma about the union/intersection of open sets?

Prove the following Lemma.

What is the corolllary about closed sets to the following Lemma.

Let A be a subset of a metric space (X,d). Define the interior A⁰ of A.

Let A be a subset of a metric space (X,d). Define the closure Ā of A.

Let A be a subset of a metric space (X,d). Define the boundary ∂A of A.

Let A be a subset of a metric space (X,d). Define the exterior A^e of A.

Are the interior, closure, boundary and exterior of A closed or open?

1. Interior - Open 2. Closure - Closed 3. Boundary - Closed 4. Exterior - Open

Finish the following two statements about the properites of a subset A ⊂ X?

Define **limits and convergence in a metric space**.

Finish the following Lemma.

Prove part (i) of the following Lemma.

Prove part (ii) of the following theorem.

What is the key to proving anything to do with limits of sequences in metric spaces?

Write down the definitions in your assumptions and aslo write precisely what you need to prove.

Define **continuity.**

What is the Lemma about the basic properties of continuous functions?

What is a preimage?

What is the theorem about continuity and open/closed sets.

Define **compact**.

What is the Lemma about convergence of subsequences?

Prove the following Lemma.

What is the proposition about clsoed sets and limits of sequences?

What is the corollary about closed sets vs. closedness?

Prove the following.

Prove the following.

Prove the following.

Define **bounded.**

What is the Lemma about compact sets and boundedness?

Prove the following Lemma.

What is the Heine-Borel for ℂ theorem?

Is the complex plane ℂ compact?

No because the sequence {ik}_k∈ℕ has no convergent subsequence

Finish the following Lemma.

What is the theorem about the continuous image of a compact set being compact?

Prove the following theorem.