Modular Arithmetic Flashcards
(27 cards)
Write a recursive algorithm for multiplication, where x,y are <=n bits long
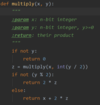
What is the running time of mult(x,y)?
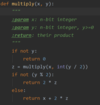
O(n^2)
each iteration might have addition on n bits - O(n)
In each iteration we remove one bit so in total we have n iterations. It sums up to O(n^2)
- Write the algorithm for recDivide*
- What is its run-time?*
Recursion depth is O(n)
each iteration takes O(n)
In total - O(n^2)
Note: n represents the size of x
The size of y does not matter
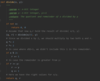
Describe the substitution rule
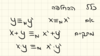
Let x,y be in the range 0 to N-1
What is the run-time of computing x+y mod N and x*y mod N?
Since x+y is between 0 and 2(N-1), we might need to substract N from the result. Thus we have addition and substractiom. O(n)
Since x*y is between 0 and (N-1)^2, this product has log((N-1)^2) bits - O(2n). to reach the remainder we need to divide the product by Mod N. in total - O((2n)^2) + O((2n^2)) = O(n^2)
Describe the modular exponentiation algorithm, its run time, and the size of its parameters.
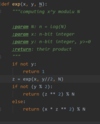
Describe Euclide’s rule
and prove it.

In order to investigate the run-time of GCD, you need to prove the following lemma:
If a>=b, then a mod b < a/2

Write GCD(a,b)
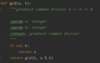
Prove the lemma:
If d divides both a and b, and d = ax + by for some integers x and y, then necessarily d = gcd(a,b)

Write the extension of Euclid’s algorithm
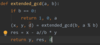
Prove the lemma:
For any positive integers a and b, the extended Euclid algorithm returns integers x, y, and d such that gcd(a, b) = d = ax + by

Define the multiplicative inverse of a modulo N.
- Does it always exist?*
- How many of them can be?*
It may not exist, as for 2 mod 6.
There can be at most 1.

Why ax mod N can be written in the form:
ax + kN?
Then, show the gcd(a, N) divides ax mod N
then, show that if gcd(a, N)>1 there can be no multiplicative inverse of a mod N
what happens when gcd(a, N) = 1
Well, that’s how we find the remainder when we compute it in out heads.
Assume we have 13 mod 6 = 1.
We think of the greatest x such that 13>6*x
it is 2. not let’s make it -2 and we have:
13 + -2*6 = 1.
Therefore, ax + kN, can surely be divide by a number y which divides both x and N, since ax/y + kN/y each returns an integer.
Assume:
- gcd(a, N) > 1.
- There exists ax such that ax mod N = 1
we also know that gcd(a,N) divides ax mod N. but no number besides > 1 divides 1. contradiction.
If gcd(a, N) = 1, by the lemma we have ax + Ny = 1. which means that ax mod N = 1. thus x is the multiplicative inverse of a mod N.
Explain what it means for a and N to be relatively prime.
gcd(a, N) = 1
recall the modular division theorem
How does it help?
This resolves the issue of modular division:
when working modulo N, we can divide by numbers relatively prime to N - and only by these. That is, if we have:
x*z = x*w (mod N)
we can divide by x to have:
z = w (mod N)
only if x is relatively prime to N.

Describe and prove Fermat’s little theorem

what is the assumption behind the Miller-Rabin algorithm
If N is prime, there are only two solutions for x^2(modN) = 1
which are, 1 and N-1.
N-1 = 2^s * t
define a, a testimony of N.
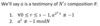
Write the Miller-Rabin algorithm

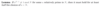

Analyze the following


Write the improve algorithm for primality

Write Lagrange’s prime number theorem and desribe the algorithm for finding a random n-bit prime number
In addition explain why checking only for a = 2,3,5 is enough
It is enough to check for a = 2,3,5 because the numbers are chosen randomly. If it wasn’t and an adversary might look for the specific case in which it fails.




