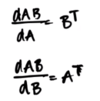Neural Networks Flashcards
1
Q
sigmoid
What does the activation function look like?
What’s the equation?
A
Output from 0-1
2
Q
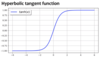
hyperbolic tangent
What does the activation function look like?
What’s the equation?
A
Output from 0-1
3
Q
What’s the logistic function?
A
Same as sigmoid
4
Q
What are some characteristics of tanh?
A
- Helps to avoid vanishing gradients problem
5
Q
Comparse sigmoid and tanh
A
Tanh converges faster
6
Q
What’s a problem with ReLU? How is it addressed?
A
Derivative at x<0 is 0
One solution: Instead use an ELU (exponential linear unit)
7
Q
Describe Relu (2) and ELU (2)
A
In general, ELU outperforms ReLU?
8
Q
What’s one thing you could do to convert a NN classifier to a regressor?
A
“chop off” sigmoid activation function and juset keep output linear layer which ranges from -infinity to +infinity
9
Q
What’s an objective function you could use for regression?
A
Quadratic Loss:
the same objective as Linear Regression –
i.e. mean squared erroradd an additional “softmax” layer at the end of our network
10
Q
What an objective function you could use for classification?
A
Cross-Entropy:
- -the same objective as Logistic Regression
- – i.e. negative log likelihood
- – This requires probabilities, so we add an additional “softmax” layer at the end of our network
- “any time you’re using classification, this is a good choice” - Matt
11
Q
What does a softmax do? (1)
A
Takes scores and transforms them into a probability distribution
12
Q
For which functions does there exist a one-hidden layer neural network that achieves zero error?
A
Any function
13
Q
What is the Universal Approximation Theorem? (2)
A
- a neural network with 1 hidden layer can approximate any continuous function for inputs within a specific range. (might require a ridiculous amount of hidden units, though)
- If the function jumps around or has large gaps, we won’t be able to approximate it.
14
Q
What do we know about the objective function for a NN? (1)
A
It’s nonconvex, so you might end up converging on a local min/max
15
Q
Which way are you stepping in SGD?
A
Opposite the gradient (verify this)
16
Q
What’s the relationship between Backpropagation and reverse mode automatic differentiation?
A
Backpropagation is a special case of a more
general algorithm called reverse mode automatic differentiation
17
Q
What’s a benefit of reverse mode automatic differentiation?
A
Can compute the gradient of any differentiable function efficiently
18
Q
- When can we compute the gradients for an arbitrary neural network?
A
(question from lecture)
19
Q
When can we make the gradient computation for an arbitrary NN efficient?
A
(lecture question)
20
Q
What are the ways of computing gradients? (4)
A
- Finite Difference Method
- Symbolic Differentiation
- Automatic Differentiation - Reverse Mode
- Automatic Differentiation - Forward Mode
21
Q
Describe automatic differentiation - reverse mode (a pro, con, and requirement)
A
- Note: Called Backpropagation when applied to Neural Nets –
- Pro: Computes partial derivatives of one output f(x)iwith respect to all inputs xj in time proportional to computation of f(x) –
- Con: Slow for high dimensional outputs (e.g. vector-valued functions) –
- Required: Algorithm for computing f(x)
22
Q
Describe automatic differentiation - forward mode (a pro, con, and requirement)
A
- Note: Easy to implement. Uses dual numbers.
- Pro: Computes partial derivatives of all outputs f(x)i with respect to one input xj in time proportional to computation of f(x) –
- Con: Slow for high dimensional inputs (e.g. vector-valued x)
- Required: Algorithm for computing f(x)
23
Q
Describe the finite difference method (a pro, con, and requirement)
When is it appropriate to use?
A
- Pro: Great for testing implementations of backpropagation –
- Con: Slow for high dimensional inputs / outputs
- Con: In practice, suffers from issues of floating point precision
- Required: Ability to call the function f(x) on any input x
- only appropriate to use on small examples with an appropriately chosen epsilon
24
Q
Describe symbolic differentiation (2 notes, a pro, con, and requirement)
A
- Note: The method you learned in high-school –
- Note: Used by Mathematica / Wolfram Alpha / Maple –
- Pro: Yields easily interpretable derivatives –
- Con: Leads to exponential computation time if not carefully implemented –
- Required: Mathematical expression that defines f(x)
25
Key thing about backprop
we're storing intermediate quantities
26
Why is backpropagation efficient?
* Reuse in the forward computation
* Reuse in the backward computation
27
What are the gradients that we store from the forward pass in backprop?
* The gradients of the objective function with respect to:
* each parameter
* The bias
28
What's one important thing to remember about back propagation?
All gradients are computed before updating any parameter values
29
Say the main steps of the pseudocode for SGD with backpropagation for a NN
30
What is y*?
The true label
31
What is y^?
The predicted label
32
* What is α(1)?
* What is its shape?
* The parameter matrix of the first layer?
* Two dimensional
33
When doing matrix multiplication, what's a useful thing to remember?
Each entry of the resulting matrix is at the row of the 1st matrix and the column index from the 2nd matrix
34
What's a fully connected layer?
layers where all the inputs from one layer are connected to every activation unit of the next layer
35
What's the difference between SGD and backprop?
* Back propagation is computing the gradients
* SGD is updating the parameters
36
What's the derivative of sigmoid, s?
s(1-s)
37
Define topological order
of a directed graph: a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
38
Say the general pseudocode for backpropagation
39
What do we know about the computation graph for a NN?
Typically a directed acyclic graph
40
What are some uses of a convolution matrix?
used in image processing for tasks such as edge detection, blurring, sharpening, etc.
41
What is the identity convolution?
Just has a 1 in the middle and zeros for every other part of the kernel, so it doesn't change the image at all (except make it smaller if you don't do any padding)
42
What's blurring convolution?
Have higher values in the middle of the kernel.
Get a blurred version of the image
43
What's the basic idea of convolution?
44
What is a stride?
Amount of pixels by which you slide the kernel at each step
45
What's the difference between CNNs and the basic feed forward NNs we've been talking about?
The CNNs have a convolution layer and max pooling layer
46
What's the key idea of CNNs?
Treat the convolution matrix values as parameters and learn them
47
What is a convolution matrix?
The matrix that has the values that are multiplied by each pixel in the inner product
48
What is downsampling?
Weights of convolution are fixed to a uniform distribution (i.e. they're all the same)
49
What is max pooling?
* A form of downsampling?
* Instead of having weights in the convolution matrix, take the max value of those in the window
50
What do CNNs use to train?
Back propagation
51
Do we minimize or maximize the objective function? What are the implications?
* The convention in this class is minimize the objective function.
* So if you need to maximize an objective function, you need to put a minus sign in front of the objective function and minimize it
52
If you have a subdifferentiable function e.g. relu what do you do to perform back prop?
Take any line in the set of the slopes of the tangent lines?
53
If you want a fully connected layer following a 3D tensor, what do you do?
Stretch the 3D tensor out into a long vector, then matrix multiply it by a weigh matrix and it will result in a linear layer
54
What is an n-Gram language model?
55
What's a key idea about RNNs?
Hidden layers are nonlinear functions of the word embeddings of every word that came before it and the word at the current time step.
56
What is the chain rule of probability?
57
how does an RNN work?
Builds up a fixed length vector representation of all the previous words
58
What's the key idea of a sequence to sequence model?
59
60
What's a fundamental assumption of ML? What are its implications?
* Assumption: Training data and test data come from the same distribution
* This allows us to make statements about theoretical guarantees and bounds on performance for hypotheses we learn
61
What do we know about true error?
It's always unknown
62
What is c\*
True function that we're trying to learn.
It labeled the training data
63
What is R^
The empirical risk minimizer
has the lowest training error
64
Does the function with the lowest expected error equal c\*, the function we're trying to model?
No because the decision boundaries each could be shaped in ways that are impossible to make for zero error.
65
What's the key idea of PAC learning?
66
What does PAC do?
What does it stand for?
67
What about PAC requires us to write the PAC criterion as a probabilistic statement?
H is trained on some random sample of our data.
68
What is sample complexity? What does it depend on?
* Minimum number of training samples we need in order to ensure that the PAC criterion is met
* Depends on epsilon and delta
69
Define consistent
Hypothesis is consistent w/ the training data if it achieves zero training error R hat of h = 0
70
What does realizable mean?
c\* is in our hypothesis space H
71
What does agnostic mean?
c\* may or may not be in our hypothesis space H
72
What does it mean for some h to be consistent with a particular training sample?
In the case of classification, It correctly classifies it
73
Describe forward propagation using one sentence
Forward Propagation is the process of calculating the value of your loss function, given data, weights, and activation functions
74
Why do we include a bias term in the input and in the hidden-layer?
Analogous to y intercept in 2d plots. It allows us to offset the fitted function from the origin.
Similar to how an intercept term in linear regression allows it to better fit data, the bias term helps the neural network better fit its data as well.
75
Why do we need to use nonlinear activation functions in our neural net?
The composition of two linear functions is itself a linear function. We want to learn more interesting patterns than what can be expressed in linear functions, and the multiplication of the inputs by the weights is a linear function. Thus, in order to make a neural network nonlinear, we need to use nonlinear activation functions.
A neural network with only linear activation functions would be no different than a linear regression. (Try forward propagating with only linear functions on the given example)
76
Which of the gradients calculated in Back propagation directly update the weights? Do not include intermediate value(s) used to calculate these gradient(s).
The gradients with respect to α and β are used in updating. The rest are intermediate values used to calculate these two gradients
77
What are two advantages of CNNs?
1. Allows us to train networks with much less data.
* Using filters slide over the input via convolution allows us to use fewer parameters while still processing the entire input through multiple layers, allowing us to train networks with much less data.
2. Since a square kernel operates on multiple rows at each time step, the 2-dimensional nature of the image is taken into account. When you flatten the image into a vector, since convolution has already been applied, the information in the 2d structure is preserved (at least partially)
78
What is translation invariance? What does it apply to?
* This allows us to use the same filter for detecting a feature **regardless of where in the image the feature occurs.**
* This is important when we want to detect a feature regardless of where it occurs in the input data.
* Applies to convolutional layers
79
What do kernels usually look like?
Often square with odd side lenghts
80
What is a kernel? What's a filter?
* ____ refers to a 2-tensor, or matrix, of weights.
* ____ refers to the set of kernels being used.
* If only one is used, then the terms filter and kernel are interchangeable.
81
What is stride?
* If you have a stride of s, you skip s-1 positions at each time step
82
* What is padding?
* Why is it used?
* adding fake values (according to one of a variety of rules)
around the borders of the image. usually applied equally to all sides of the image
* Helps ensure each part of the kernel is applied to each part of the image
83
What effects the output size of a given layer? (4)
Input size, filter size, stride, and padding
84
What is the tradeoff of different stride values?
Smaller stride -\> more information, but requires more computation and produces more output data
85
What do we know about stride values? (1)
Usually have the same stride value in all dimensions
86
How many positions can the kernel fit when S=1 and p=0
* horizontally?
* Vertically?
* H - K + 1
* W - K + 1
87
What's the scope of kernels and filters in this class
We're only dealing with situations in which our filter consists of one kernel applied to one channel at a time.
88
In the case of our NN, what is
* α
* a
* z
* β
* y hat
* x subzero
* z subzero
* α - matrix of weights from inputs to the hidden layer
* a - input data times the weights
* z - output of the activation function applied on a
* β - matrix of weights from the hidden layer to the output layer
* y hat - output layer
* x subzero - bias at the input
* z subzero - bias at the hidden layer
89
What's the correspondence between alpha and z?
Each row in the alpha matrix corresponds to one unit in the hidden layer z.
90
What is x hat?
It's our x matrix with a bias term added in
91
What's the derivative of a matrix multiplication with respect to one of the input matrices?
A transpose of the other input matrix (not the one you're taking the gradient with respect to)
92
How do we know that our gradient matrix is the right shape during back propagation?
Shape of the gradient matrix = shape of the matrix that you're taking the gradient with respect to (if it's differentiating a scalar)
93
What's the intuition behind the dimensions of a weight matrix? One rule for row and one for columns
* # of rows = # of neurons in the previous layer
* # of columns = # of neurons in the next layer
94
How are neural networks able to approximate nonlinear functions?
To extend linear models to represent nonlinear functions of x, we can apply the linear model not to x itself but to a transformed input φ(x), where φ is a nonlinear transformation
95
In simple terms, what do activation functions do?
Compute the hidden layer values
96
What's one way to describe the limitation of linear functions?
Linear models can't understand the interaction between any two input variables.
97
Is a Relu linear?
No, it's nonlinear. However, the function remains very close to linear, in the sense that is a piecewise linear function with two linear pieces. Because rectified linear units are nearly linear, they preserve many of the properties that make linear models easy to optimize with gradientbased methods
98
Why is ReLU popular?
* rectified linear units are nearly linear, they preserve many of the properties that make linear models easy to optimize with gradient-based methods.
* They also preserve many of the properties that make linear models generalize wel
99
What do we know about optimization for a neural network? (1)
the nonlinearity of a neural network causes most interesting loss functions to become non-convex
100
* For feedforward NNs, What values should weights be intialized to?
* What about biases?
* For feedforward neural networks, it is important to initialize all weights to small random values.
* The biases may be initialized to zero or to small positive values
101
How do we know the number of features by looking at a neural network diagram?
It's the number of input nodes
102
Describe how adagrad works (2)
* Adagrad implicitly changes the step size based on the shape of the function inferred from the gradients.
* Each parameter has its own learning rate that improves performance on problems with sparse gradients.
103
What does adagrad do? (1)
Learning rate decreases slowly over time
104
What's the reason for using adagrad?
We want to use a large step size (aka learning rate) where possible, but smaller LR where we are in danger of overshooting the optima.
105
How many neurons are there in the input layer?
=The number of input variables
106
How many neurons are there in the output layer?
The number of outputs associated with each input
107
How do you calculate the number of neurons in a hidden layer? (5)
1. Based on the data, draw an expected decision boundary to separate the classes.
2. Express the decision boundary as a set of lines. Note that the combination of such lines must yield to the decision boundary.
3. The number of selected lines represents the number of hidden neurons in the first hidden layer.
4. To connect the lines created by the previous layer, a new hidden layer is added. Note that a new hidden layer is added each time you need to create connections among the lines in the previous hidden layer.
5. The number of hidden neurons in each new hidden layer equals the number of connections to be made.
108
How do we know if hidden layers are required in a neural network?
hidden layers are required if and only if the data must be separated non-linearly.
109
What is a component of that ANNs are built from?
A single layer perceptron
110
* What's the perceptron equation?
* What do we know about single layer perceptions? (1)
* y = w\_1\*x\_1 + w\_2\*x\_2 + ⋯ + w\_i\*x\_i + b
* It's a linear classifier
111
* How do we represent neural network decision boundaries?
* What's the intuition behind this?
* By using multiple lines.
* ANN is a multilayer perception. Each perception adds a line. Each perceptron/line corresponds to one neuron in the hidden layer?
112
How do you figure out the decision boundary for a neural network?
* Draw the ideal decision boundary curve
* One line intersection needs to represent each change in direction of the ideal DB curve. Add lines accordingly
* The output layer does the merging of the two lines
113
For regularization, what is:
* Alpha
* Omega(theta)
* lambda
* from 0 to infiniti, - a hyperparameter that weights the relative contribution of omega(theta)?
* parameter norm penalty term, omega(theta)
* (fill this in)
114
What's interesting about how regularization is applied? Why does this happen?
for neural networks, we typically choose to use a parameter norm penalty Ω that penalizes only the weights of the affine transformation at each layer and leaves the biases unregularized. The biases typically require less data to fit accurately than the weights. Each weight specifies how two variables interact. Fitting the weight well requires observing both variables in a variety of conditions. Each bias controls only a single variable. This means that **we do not induce too much variance by leaving the biases unregularized.** Also, regularizing the bias parameters can introduce a significant amount of underfitting.
115
How does weight decay relate between layers of the neural networks?
Because it can be expensive to search for the correct value of multiple hyperparameters, it is still reasonable to use the same weight decay at all layers
116
What kind of penalty do we use for the regularization of neural networks?
it is sometimes desirable to use a separate penalty with a different α coefficient for each layer of the network
117
What is ridge regression?
synonymous with L2 regularization
118
What is Tikhonov regularization?
Synonymous with L2 regularization
119
What is weight decay?
Name for the L2 parameter norm penalty, not for L2 regularization in general?
120
What's the difference between L2 regularization and weight decay?
121
What does L2 regularization do? (2)
* drives the weights closer to the origin1 by adding a regularization term to the objective function
* Only directions along which the parameters contribute significantly to reducing the objective function are preserved relatively intact.
122
What's the penalty term Omega(theta) of L2 regularization?
123
For L1 regularization, what is Omega(theta)?
The L1 norm of ω
124
What is the L1 norm?
The sum of absolute values of the individual elements of the vector
125
* Compare how the regularization contribution to the gradient compares between L1 and L2 regularization.
* What's the implication?
* For L1, the regularization contribution to the gradient doesn't scale linearly with each lowercase omega sub i; instead it is a constant factor with a sign equal to sign(lowercase omega sub i).
* One consequence of this form of the gradient is that we will not necessarily see clean algebraic solutions to quadratic approximations of J(X, y;lowercase omega) as we did for L2 regularization
126
What do L1 and L2 regularization have in common?
* Generally, they shift the values of lowercase omega toward zero.
* Technically, it doesn't have to be zero in either case, but that's usually how it's implemented
127
For regularization, what is ω?
128
Compare the solutions of L1 and L2 regularization. (1)
* L1 results in a solution that is more sparse
129
In what case does L1 regularization cause parameters to become sparse (i.e. 0)?
What about L2?
* In the case of a large enough α
* Never
130
What is L2 regularization equal to? (not a synonym)
MAP Bayesian inference with a Gaussian prior on the weights
131
At a high level, what is the goal of regularization? (1)
* reduce the test error (i.e. increase its ability to generalize), possibly at the expense of increased training error
132
In SGD, does the direction that you're stepping relative to the gradient change based on whether you're minimizing or maximizing the objective function?
133
In forward propagation, what happens at each layer?
Given the input data x, we multiply it by the given weights, α, then apply the corresponding activation function to it and finally pass the result to the next layer
