Outer Measures Flashcards
(18 cards)
u is a measure
<=>
“squeeze”
1) u(Ø) = 0
2) A_i finite, disjoint
3) B_i uncountable, not nec disjoint
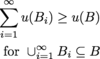
what’s an outer measure on a set X?
ü: P(X) -> [0, ∞]
1) ü (ø) = 0
2) ü(A) <= ü(B)
if A is in B
3) “countably subadditive”
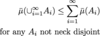
a subset E of X is ü-measurable if
for all A in X,
ü(A) = ü(A n E) + ü( A n Ec)
If ü(E) = 0, then …
E is ü-measurable
called “null set”
The collection of ü-measurable sets is…
a σ-algebra
If E1, E2, …, En are disjoint and measurable then…
nice property
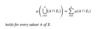
Carathéodory, u* is defined as…
u*(A) = ∞, if no sequence in S covers A

u*(A) is blah to u(A)
less than or equal to
E ü-measurable is equivalent to
u(A) => u*(A n E) + u*(A n Ec)
for all A in S, with u(A) < infinity
For all E in S, is E u*-measurable?
YES
A n Ec = C1 u C2 u … u Cn,
can show u(A) => u*(A n E) + u*(A n Ec)
Lebsgue Stieltjes Measure
u_f : S –> [0, ∞]
by u_f ( [a, b] ) = f(b) - f(a)
for f increasing, left continuous real function
open set E
for every x in E
there exists a ball around x contained in E
closed set E
complement is open
or
every convergent sequence of points in E,
has a limit in E
“sequentially closed”
measures and sequences:
if

if A_i is in a σ-algebra
then u(A_i) approaches u(A)
Borel Sets
σ-algebra generated by open sets in R
Cantor Set
throw away middle thirds :
C_1 = [0, 1] - (1/3, 2/3) …
Cantor set is compact
length 0
as many points as R
lebesgue measure, lambda
lambda( [a, b) ) = b - a
“for Rn”
it’s
lambda( [a, b) x [a, b) ….) = (b-a) * (b-a) *…
Vitali is
an example of a non lebesgue-measurable
subset of R
(can’t acutally construct it)
need axiom of choice


