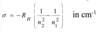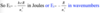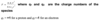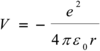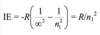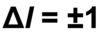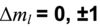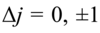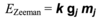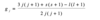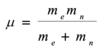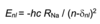Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

CHEM0005 > Physical > Flashcards

Physical Flashcards

1
Q

Describe atomic spectroscopy

A

The study of the absorption and emission of photons by atoms. Experimental observation prompted the idea that energy is quantised.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Give the equation that governs which energies are possible for the hydrogen atom and explain all the terms

A

E is measured in joules

h is planck’s constant

c is the speed of light

Rh is the Rhydberg constant for the H atom

n is the principle quantum number

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Describe what happens when an electron is excited to a higher energy state

A

The atom absorbs a specific amount of energy equal to the separation of the levels. (E2-E1 = hf = hv - h is planck’s constant and f is v (nu) is the frequency)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Describe what happens when an electron drops down to a lower energy state

A

The atom emits a specific amount of energy equal to the separation of the levels (E2-E1 = hf = hv - h is planck’s constant and f is v (nu) is the frequency)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

State the equation for photon energy

A

Photon energy = hf = E2 - E1 = hv (should be a very small number) E2 is the higher energy f is v (nu) is the frequency

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Describe absorption spectra

A

Absorption spectra measure the wavelengths of light that are absorbed by a sample, as the atoms take up energy and move to higher energy levels. All species start in their ground state

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Describe how emission spectra are obtained

A

Energy is put into a sample of atoms to excite them to higher levels. The wavelengths of the light emitted when the atoms give up energy and drop back down is measured

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Describe how energy is given to a sample of atoms in emission spectra

A

The sample is heated or an electrical discharge is applied

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

State the four components needed to carry out a typical absorption spectroscopic experiment

A
  • a light source
  • a sample
  • a wavelength selecting element
  • detector
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Describe the light source needed in a typical absorption spectroscopic experiment

A

As there has to be a broad range of wavelengths produced, white light is used

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Describe the sample needed in a typical absorption spectroscopic experiment

A

The sample normally has to be gaseous, which means it must be heated beforehand

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Describe the wavelength selecting element needed in a typical absorption spectroscopic experiment and give two examples.

A

This is needed to disperse the light that has passed through the sample, in order to see which wavelengths of light have been absorbed. A prism or a diffraction grating may be used.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Describe the detector needed in a typical absorption spectroscopic experiment

A

In the past, photographic plates were used but now highly sensitive cameras are more common. Sometimes the selecting element is rotated and a point detector is used.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Describe the setup of a typical emission spectroscopic experiment

A
  • A sample
  • a wavelength selecting element
  • detector

The sample is excited and the wavelength selecting element disperses the wavelengths.

The setup is almost the same as that of an absorption spectroscopic experiment, but without the light source.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Describe atomic spectra

A

The lines show how the electronic energy of atoms is quantised. Different atoms have different spectra, so they can be used to identify elements

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Name in order the EM spectrum starting from the lower energy waves

A

Radiowaves, microwaves, infrared, visable, ultra violet, x-rays, gamma rays

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Define an electron volt (eV)

A

The energy gained by the charge of a single electron moved across an electric P.D of one volt. It is 1.602x10-19 J

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Describe how to convert from joules to eV

A

Divide energy in joules by the value of 1 eV

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

State the fundamental equation for the speed of an EM wave

A

c = fλ

c is the speed of the wave f is the frequency λ is the wavelength

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

State the multiplier for the prefix ‘nano’

A

10-9

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Define one Å

A

Å represents ‘angstrom’. One angstrom = 1x10-10m

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Define wavenumber (v~) and relate it to photon energy

A

1/λ, measured in (length)-1. We can get E = hcv~, so photon energy is proportional to wavenumber. It is an energy equivalent unit

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

State how to convert from m-1 to cm-1

A

Divide by 100

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

Describe the emission spectra of the hydrogen atom

A

There are many lines which are clearly in groups (ie series), with each series of lines converging with decreasing wavelengths/ an increasing photon energy. All lines in a series have the same value of n1. The names correspond to the scientists who observed them.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

Give Bohr’s equation for wavenumber and explain the terms

A

RH is the Rydberg constant for the hydrogen atom.

n2 is the quantum number of the upper level of the transition and n1 the number of the lower level. n2 > n1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

State the names of the first four series and their values of n1

A

Lyman (n1 = 1), Balmer (n1 = 2) , Paschen (n1 = 3) and Brackett (n1 = 4)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

Describe Bohr’s explanation of his equation for wavenumber

A

He said the electron orbiting the nucleus must be confined to specific orbits of fixed energies, with each orbit having a different value of n

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

Give the energy level expression for the hydrogen atom in joules and wavenumbers

A

n is the principle quantum number

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

Define the zero of energy

A

Also known as the ionisation limit, where n = ∞, this is defined as a separated proton and electron. From this we can see why orbital energies are negative.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

Describe how to determine the value of R in the energy level expression for an atom

A

Start by looking at values of wavenumber of lines in one series; all values of n1 will be the same so 1/n12 can be labelled as a constant c. Now the Bohr equation resembles that of a straight line, and -R can be found by calculating the gradient of this line

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Describe the Rydberg constant

A

Rx is calculated using values of wavenumber for a particular atom. It differs slightly for different atoms.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

Describe Bohr’s three postulates that quantitatively explain the energy level equation for the hydrogen atom

A
  • Electrons move in circular orbits around the nucleus
  • Only certain orbits are allowed, ie those with integer values of n. While in these orbits, electrons do not emit energy.
  • A single photon is emitted or absorbed when an electron moves into a different orbital
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

Give the equation that gives the force required to keep a particle in its circular orbit and explain the terms

A

F = force

m = mass of the particle

v = velocity of the particle

r = radius of the orbit

Note the negative sign: force is in the opposite direction to the radius, ie it points towards the centre of the orbit

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

Give the equation for linear momentum

A

p = mv

p = momentum

m = mass

v = velocity

35
Q

Describe angular momentum

A

It is a vector quantity and its direction is perpendicular to the plane of rotation. It is important as electrons and photons have angular momentum which is usually conserved in chemical processes.

36
Q

Give the equation for angular momentum and explain the terms

A

L = Iω

I is the moment of inertia; the angular equivalent of mass

ω (omega) is the angular velocity in rads-1

37
Q

Describe I, the moment of inertia

A

l is the sum over all the masses that make up the body multiplied by the square of their distance from the axis of rotation. Ie heavy objects with a lot of mass far from the axis of rotation have a large moment of inertia

38
Q

Describe kinetic energy and give its equation

A

Kinetic energy is energy due to movement and is equal to 1/2mv2

39
Q

Describe potential energy (V)

A

V is energy because of a position in a field. It is a relative quantity and is calculated by how much work is takes to move the object from a defined ‘zero state’.

40
Q

State coulomb’s law and explain its use and its terms

A

This equation tells us about the force between two charged species.

41
Q

State Bohr’s postulate relating to the quantisation of the angular momentum of the electron

A

Bohr said the angular momentum of the electron had to have values of multiples of h/2⫪, = ℏ. Ie nℏ where n was the quantum number. Note; if we rearrange this to get v, it is shown that the velocity of the orbiting electron is also quantised.

42
Q

Describe the zero state and potential energy of the hydrogen atom.

A

‘Zero State’ is defined as infinite separation. As the electron gets closer to the nucleus, P.E becomes negative. Work has to be done on the system to separate the electron and the proton; work done to move an electron from a distance r from the nucleus to infinite separation is measured in joules and equal to -V

43
Q

Describe kinetic energy and give its equation

A

Kinetic energy is energy due to movement, and is equal to 1/2mv2

44
Q

State the two types of energy an object can have

A

Kinetic and/or potential

45
Q

Give the equation for potential energy (V) of an electron and explain the terms

A

e is the fundamental charge, 1.602 x 10-19 C

ε0 is the permittivity of free space, 8.854 x 10-12 Fm-1

r is the radius

46
Q

Define the ionisation energy of an atom

A

The energy required to remove an electron from the ground state of the atom to an infinite distance.

47
Q

Define the ionisation energy of an orbital

A

The energy required to remove an electron from that orbital to an infinite distance, ie exciting the electron from that orbital to one with n = ∞

48
Q

Give the equation for the ionisation energy of an electron in a specified Hydrogen orbital

A

Note: for all atoms except hydrogen, this equation must be multiplied by Z2

This equation gives IE in cm-1

49
Q

Describe the principle quantum number, n

A

n can take any positive integer value. For the H atom, it determines the energy.

50
Q

Describe the orbital angular momentum quantum number, l

A

l tells us about the orbital angular momentum of the electron, ie how fast the electron orbits the nucleus. l can take integral values from 0 to n-1

51
Q

Describe the magnetic quantum number (ml)

A

ml tells us the component of the orbital angular momentum along the z-axis, and that component is quantised. ml can take integer values between and including -l to +l.

52
Q

Give the meaning of ‘the orientation of l is quantised’

A
53
Q

Give the equation for the magnitude of the orbital angular momentum, ie the length of l

A
54
Q

State the selection rule for n in an absorption spectrum

A

There is no restriction on the change of n

55
Q

State the selection rule for l in an absorption spectrum

A
56
Q

State the selection rule for ml in an absorption spectrum

A
57
Q

Describe the transitions in absorption

A

1s –> np

58
Q

State how many independent wavefunctions/orbitals there are for any value of l

A

For a given value of l, there are 2l+1 independent wavefunctions/orbitals.

59
Q

Give the factor by which the strength of the spin-orbit interaction increases

A

Z4

Therefore, splittings are more obvious with heavier atoms

60
Q

Define the total angular momentum quantum number, j

A

j comes from combining the orbital l and spin angular momentum s.

j = l+s, l+s-1, … |l-s| - this is a Clebsh-Gordon Series

j is quantised

61
Q

State the value of s when we are dealing with just one electron, eg in an H atom

A

s = 1/2

62
Q

Give a standard term symbol

A

2s+1lj

l is given as a capital letter, ie if l = 0, it is written as S

Note that for multi-electron atoms, total spin angular momentum and total orbital angular momentum are obtained by combining s and l values of all the electrons.

63
Q

State the selection rule for s

A
64
Q

State the selection rule for j

A
65
Q

Describe the fine structure of a transition

A

The fine structure of a transition is due to spin-orbit coupling. Splitting patterns are very small and observing them requires high-resolution spectroscopic techniques.

66
Q

Describe the quantised orientation of j, mj

A

mj can take values from j down in steps of 1 to -j

Note that in the absence of an external field, all mj sublevels of a given j state are degenerate

67
Q

Describe how the degeneracy of the mj levels is affected in an external field, ie in a magnetic or electric field

A

The degeneracy of the mj levels is removed and the atomic spectra exhibit many more lines

68
Q

Describe the Zeeman effect

A

The Zeeman effect refers to the increased complexity of the atomic spectrum in a magnetic field

69
Q

Describe the Stark effect

A

The Stark effect refers to the separation of the mj levels due to an electric field

70
Q

Describe the anomalous Zeeman effect

A

The anomalous Zeeman effect applies to atoms which have non-zero spin angular momentum, s>0

71
Q

Give the equation giving the energies of the mj sublevels of a given j state in a magnetic field

A

k is a constant which depends on the size of the magnetic field (B) and other constants.

gj is the Lande g - factor

Splitting is proportional to mj so larger values of mj are shifted the most, and positive values of mj are shifted to higher energy, and visa versa

72
Q

Define the Lande g - factor

A

The splitting between the different mj levels of a given j state at a given field is given by gj.

Larger values of gj mean larger amounts of splitting.

The values of l, j and s put into the equation are the values for the level we are considering

73
Q

Give the equation for the reduced mass of a system, μ

A

me is the mass of an electron and mn is the mass of the nucleus

74
Q

State the selection rule for mj

A
75
Q

State the contribution of a closed (ie complete) shell to the angular momentum of an atom

A

A closed shell contributes no angular momentum to an atom

76
Q

Describe how to construct term symbols for multielectron atoms

A

Only electrons in partly filled orbitals are considered.

S and L are the total spin and orbital angular momentum of the atom, and si and li are the spin and orbital angular momentua of the electrons of interest, i = 1,2,3…

S and L are combined to give J

77
Q

Define δnl

A

δnl is called the quantum defect. Its value heavily depends on l and very weakly depends on n.

It quantifies the degree of penetration of an electron in a given orbital.

78
Q

Give the energy level expression used to model the spectra of sodium

A
79
Q

Describe how term symbols for the helium atom are worked out

A

We use a Clebsh-Gordon Series to combine the spins and orbital angular momenta of the individual electrons to get S and L

S = s1+s2, s1+s2-1, |s1-s2|

L = l1+l2, l1+l2-1, |l1-l2|

80
Q

State and describe the selection rules for multi-electron atoms

A

The selection rules for S and J are the same as those for s and j, note that the selection rule for L is different to that of l

ΔS = 0

ΔJ = 0, ±1

ΔL = 0, ±1

81
Q

State the name for states with S = 1

A

Triplet states, as 2S + 1 = 3

82
Q

State the name for states with S = 0

A

Singlet states, as 2S + 1 = 1

83
Q

Give μ for an infinitely heavy nucleus

A

μ = me

For the case that me<<m>n</m>

CHEM0005 (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions