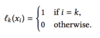Polynomial interpolation Flashcards
What is the main question in polynomial interpolation?
How do we represent mathematical functions on a computer?
Why are polynomials easy to store?
Only need to store n + 1 coefficients
What is the Weierstrass Approximation Theorem?
What is interpolation?
Finding a pn(xi) = f(xi) at a finite set of points xi called nodes. Sometimes we also require the derivatives to match.
What is the simplest interpolating polynomial?
Truncated taylor series
Why is a truncated Taylor series the simplest interpoalting polynomial?
It uses only a single node x0
What is Taylor’s Theorem?
What is the following known as?
Taylor polynomial of degree n
What is the remainder in Taylor’s theorem called?
Lagrange form of the remainder
What is the formula for the Lagrange form of the remainder?
What can we use to bound the error of an approximation using Taylor’s theorem?
The Lagrange remainder
What is truncation error?
The error that arises from approxiamting f with a truncated series, rather than due to rounding
How does truncation error change as you use more terms?
It decreases
What is Rolle’s Theorem?
Prove the Lagrane form of the remainder.
For general n, what are the polynomial interpolation conditions?
What is another way to write the following conditions?
What is the following called?
The Vandermonde matrix
What is the Vandermonde matrix?
What is the determinant of the Vandermonde matrix?
Prove that the determinant of the Vandermonde matrix is the following.
Problem Sheet
What is the existence/uniqueness theorem for interpolating polynomials?
Prove the unique part of the following theorem.
What is one way to solve the Vandermode matrix?
Gaussian elimination
What basis do we use in the Vandermode matrix?
{1, x, x2 .. }
When we use the basis of polynomials {lk} what does pn(x) equal?
For general n, what is the equation of the n+1 Lagrange polynomials?
What is a problem with the Lagrange form of the interpolating polynomial?
- Expensive to evaluate since all the lk must be computed
- Chaning any nodes or adding a new node means all the lk must all be recomputed from scratch
How is the basis {lk} picked?
So that we get the identity matrix meaning we get the following pn(x). So we need the following.
What is the main idea for the Newton form of the basis?
Find a basis where pn+1 = pn + gn+1(x) so that adding new nodes is easier than the lagrange form os the basis
What is the formula for the {nk} in the Newton basis.
What is the Newton form of the interpolating polynomial?
What is the the other notation which is commonly used for ak in the Newton form of the interpolating polynomial?
ak = f[x0,x1, …, xn]
What is the theorem about the divided differences?
Prove the following theorem.
What do the diagrams for the Newton form of the interpolting polynomial look like?
Tree diagrams
What is the generic error for an interpolating formula?
f(x) - pn(x) |
What is Cauchy’s theorem for the error in an interpolating formula?
Prove the following theorem.
How do you find what the maximum value of the error in Cauchy’s formula?
The maximum of the node polynomial w(x) occurs at a turning point or at an end point, so find and use that value of x.
What is the formula for w(x), the node polynomial?
What is the Runge phenomenon?
When pn converges to f in the middle, but diverges more and more near the ends.
What type of nodes do we choose to avoid the Runge phenomenon?
Chebyshev nodes
How do the spacing of chebyshev nodes change?
Places more nodes at the end of the interbal where most of the error is occuring at
What is the xj formula to find the Chebyshev nodes?
What is the Lemma about the Chebyshev points?
Prove the following Lemma.
What is the theorem about Chebyshev interpolation?
Prove the following theorem.
What are the Chebshev nodes projections of?
Equally spaced points around a circle
What is the upper bound for the error in a Chebyshev polynomial?
What is the basic idea behind adding derivative conditions to interpolating polynomials?
Find polynomial that match one or more derivatives of f at the nodes, as well as function values
What two interpolating polynomials have derivative conditions?
- Taylor polynomial
- Herminite polynomial
What is the theorem about Hermite interpolation?
Prove the following theorem.
What is the formula for the Hermite basis functions?
What is the formula for the Hermite interpolating polynomial?
