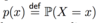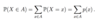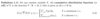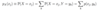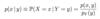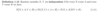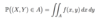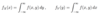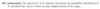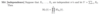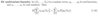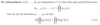Preliminaries Flashcards
Define a sample space.
A sample space Ω is a collection of all possible outcomes of a probabilistic experiment.
What symbol represents a sample space?
Ω
Define an event.
An event is a collection of possible outcomes.
What symbol represents the impossible event?
∅
What symbol represents a certain event?
Ω
Define a field.
Are fields open or closed w.r.t. taking finite unions or intersections?
Closed
Define a σ-field.
What can you replace property 2 by in the following?
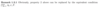
What is the smallest σ-field in Ω?
{∅,Ω}
What is the biggest σ-field in Ω?
All the subsets of Ω.
Define a probability distribution.
What are the A1-A4 properties of a probability distribution?
What are the P1-P3 properties that following on from the following properties?
Define a probability space.
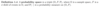
What is another name for a probabiluty space?
Probability measure.
What is the pair (Ω,𝑭) called?
Measurable space
Finish the following lemma.
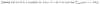
Prove the following Lemma
Need to take photo.
Define conditional probability.
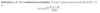
What is P4 - the multiplication rule for probabilities?
What is P5 - partition theorem or formula of total probabilities?
What is P6 - Bayes’ theorem?
Define independent.
Define mutually independent.
Define a random variable, X.
If the sample space of possible outcomes is a set of real outcomes, then the outcome to the probabilistic experiment is called a random variable.
What is the probability distribution of a r.v. X?
The collection of probabilites ℙ(X ∈ A) for all intervals A ⊆ ℝ.
When is X a discrete r.v.?
If in addition Ω is countable, i.e. if the possible values for X can be enumerated in a (possiby infinite) list.
What is the probability mass function of a discrete r.v. X?
What is the probability distribution when X is a discrete r.v.?
What is the probability distribution for a continuous r.v. X?
Define the cumulative distribution function.
Define a multivariate random variable.
What is the joint probability distribution of (X,Y)?
What is the marginal probability distribution of X in a joint distribution?
What is the probability mass function for the conditional distribution of X given Y?
What is the r.v. version of the partion theorem called?
Law of total probability.
What is the law of total probability?
If X and Y are independent what does p(x,y) factorise to?
Define when two random variable X, Y are independent.
What is the continuous probability density function for a joint distribution of (X,Y)?
What are the marginal pdfs for the joint, continuous r.v. (X,Y)?
What is the continuous conditional density distribution of X given Y?
Define the expected value.
What are the names of the four important properties of expectation?
- Linearity
- Monotonicity
- Multivariate linearity
- Independence
What is the equation for variance?
Define conditional expectation.
What is the E1 - linearity - property of expectation?
What is the formula for covariance?
What does covariance equal to show two varaibles are uncorrelated?
0
What does the following equal?
What does the following equal when the variables are pairwise uncorrelated?
What is the partition theorm for expectation?
What is the law of large numbers theorem?
What is the central limit theorem?
Define the moment generating function.
What are the name of the five useful properties of the moment generating function?
- Expectation
- Uniqueness
- Linear transformation
- Independence
- Convergence
What is the M1 - expectation - property of moment generating functions?
What is the M2 - uniqueness - property of moment generating functions?
What is the M3 - linear transformation - property of moment generating functions?
What is the M4 - independence - property of moment generating functions?
What is the M5 - convergence - property of moment generating functions?
What is the E2 - monotonicity - property of expectation?
What is the E3 - multivaraite independence - property of expectation?
What is the E4 - independence - property of expectation?
