Quant Flashcards
Using the last digit shortcut, find the units digit of (72)(92)(33) . . .
7 x 7 = 49; drop the tens and keep only the digit 9
9 x 9 = 81; drop the tens and keep only the digit 1
3 x 3 x 3 = 27; drop the tens and keep only the digit 7
9 x 1 x 7 = 63; the units digit of the final product is 3
When testing cases in Data Sufficiency, try F0N1S numbers. . .
Fractions
(0) Zero
Negatives
(1)
Square Root
An integer is divisible by
5 if:
The integer ends in 0 OR 5
e.g. 75 or 80
Cylinder Volume?
V = π r2 h
- What happens when you increase the numerator of a fraction while holding the denominator constant?
- Increase the denominator while holding the numerator constant?
- Add the same number to both the numerator and denominator?
- Approaches infinity, increases in value
- Approaches 0
- Approaches 1, no matter if the fraction is larger than 1 or smaller than 1
Note:
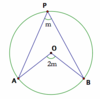
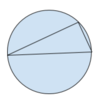
If one of the sides of a triangle inscribed in a circle is a diameter of the circle, then the triangle must be a right triangle.
Rate x Time = Distance
Set-up the chart to solve for an average when you know the going and the return rates, and the total distance
- Working together: add the rates
- Running away: subtract the rates
- Chasing each other: subtract the rate
An integer is divisible by
6 if:
The integer is divisible by both 2 AND 3
e.g. 48
Prime Factors: 2, 2, 2, 2, 3
What is the Quant Timing Strategy?
Complete 8 questions every 15 min.
Common relationships in word problems:
- Total Cost = Unit Price x Quantity Purchased
- Profit = Revenue - Cost
- Total Earngings = Wage Rate x Hours Worked
- Miles = Miles per Hour x Hours
- Miles = Miles per Gallon x Gallons
What is the greatest common factor?
Between 100, 140, and 250
The greatest number that divides evenly into the two numbers.
Factor them down to Prime Factors
100: 2, 2, 5, 5; 22, 52
140: 2, 2, 5, 7; 22, 51, 71
250: 2, 5, 5, 5; 21, 53
Look at the minimum from each column the numbers have in common; 21 x 51 = 10
Set-up the chart to determine overlapping sets between men, women, and employees. . .
- Pay attention to sub-sets of sub-sets wording
- Look out for given contraints (when there is a null value inherent)
Note:
- When absolute value of variable is less than, the answer will be -4
- When absolute value of variable is greater than, the answer will be x > 2 or x
- x > 2 or x
| 2x + 2 |
- -4
2x + 2 | > 6
What are the 3 special products of quadratic expressions?
- x2 - y2 = (x + y)(x - y)
- x2 + 2xy + y2 = (x + y)(x + y) = (x + y)2
- x2 - 2xy + y2 = (x - y)(x - y) = (x - y)2
* Look out for sq. roots hidden as special quadratic expessions. Look to use substiution to solve quickly.
Note:
For some probability problems it may be easier to calculate the probability of something NOT occurring.
A bag contains R, G, B and Y marbles. 3 marbles are pulled, what is the probability at least 1 will be red.
Not Red:
2/3 X 2/3 X 2/3 = 8/27
Red:
1 - 8/27 = 19/27
Even * Even =
Odd * Odd =
Even * Odd =
Even * Even = Even^
Odd * Odd = Odd
Even * Odd = Even^
^ If one Even number is present, the result will be Even. If only Odd numbers exist, the result will be Odd
An integer is divisible by
3 if:
The sum of the integer’s digits is divisible by 3
e.g. 72 = 7 + 2 = 9
9 is divisible by 3
e.g. 83 = 8 + 3 = 11
11 is not divisible by 3
Circle:
Circumference?
Diameter?
Radius?
Area?
C = π • d
d = 2 • r
⇒ C = 2 • π • r
A = π • r2
An integer is divisible by
9 if:
The sum of the integer’s digits is divisible by 9
e.g. 4,185 = 4 + 1 + 8 + 5 = 18 / 9; yes
Note:
- If you are given two sides of a triangle or parallelogram, you can maximize the area by placing those two sides perpendicular to each other
What is the factor foundation rule?
If A is a factor of B, and B is a factor of C, then A is a factor of C
e.g. since 72 is divisible by 12, 72 is also divisible by all the factors of 12 (1, 2, 3, 4, 6, 12)
Cylinder Surface Area?
SA = 2 • π • r2 + 2 • π • r • h
What is the area of a Trapezoid?
What is the area of a any polygon?
- [(Base1 + Base2) x Height] / 2
- Base x Height
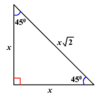
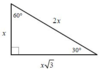
What are the common combinations of right triangles?
* Watch out for imposters; a non-right triangle with a side of 3 and a side of 4 does not have a third side of length 5.
What are the legs of a 45 - 45 - 90 triangle?
If given the hypotenuse to get a leg divde by sq. root 2
What are the legs of a 30 - 60 - 90 triangle?
If given the hypotenuse to get the short leg multiply by sq. root 3, divide by 2
If given the hypotenuse to get the long leg divide by 2
Count of multiples of 3 between 1 and 150. . .
What is their sum?
Number of terms = (Last - First) / Increment + 1
(150 - 3) / 3 + 1 = 50
- Make sure to use only the multiples of the increment as the first and last numbers
Average of Set = (First + Last) / 2
(3 + 150) / 2 = 76.5
Multiply Number of Terms x Average of Set
50 x 76.5 = 3,825
Note:
When looking to calculate the distance between two points on a coordinate plane, look for special triangles
Use an anagram grid to describe:
7 people enter a race, 4 medals given, winner gets Platinum, 2nd gets Gold, 3rd gets Silver, the rest get bronze
7 = number of places
1 = number of Platinum
1 = number of Gold
2 = number of Silver
3 = number of Bronze
Is an integer X divisible by 9?
- Find Prime Factors in problems of divisibility
X = 210
Prime Factors: 2, 3, 5, 7
No because there are not two 3’s in the within the prime factors
In Combinatorics, what do “OR” and “AND” mean?
A restaurant has 3 main dishes: S, C, and F and 2 side dishes: P and D
- How many different combinations exist?
OR: (S + C + F) = 3
AND: (P + D) = 2
3 * 2 = 6
Watch for the disguised quadratics:
3x2 = 6x
3x2 = 6x
3x2 - 6x = 0
3x ( x - 2) = 0
x = 0 or x = 2
Memorize Cubes and Cube Roots
13 = 1
23 = 8
33= 27
43 = 64
53 = 125
103 = 1,000
What is true of Central angles related to inscribed angles?
An inscribed angle is equal to half of the arc it intercepts, in degrees.
Note:
Don’t forget adding the inequalities is a solution
*Make sure the signs face the same way
3x + 4y > 9
3x - 2y > 3 –> 6x - 4y > 6
9x > 15
x > 5/3
An integer is divisible by
8 if:
The integer is divisible by 2 three times
OR
the last three digits are divisible by 8
e.g. 24,856 = 856 / 8; yes
What is true about any two sides of a triangle in relation to the third?
The sum of any two sides of a triangle must be greater than the third side.
Equation for the sum of interior angles of a polygon. . .
(n - 2) x 180
*n is the number of sides
On the GMAT, it generally pays to factor exponential terms that have bases in common:
If x = 420 + 421 + 422, what is the largest prime factor of x?
x = 420 + 421 + 422
x = 420 (40 + 41 + 42) → Remember that this is an option to simplify the exponent
x = 420 (1 + 4 + 16)
x = 420 (21)
x = 22 x 20 (3 x 7)
7 is the largest prime factor.
Work Backwards as a strategy
Start with the answer choices and solve the problem using the constraints
* When you get a match while working backwards, that is your answer
Note:
- Of all quadrilaterals with a given perimter, the square has the largest area
An integer is divisible by
10 if:
The integer ends in 0
An integer is divisible by
4 if:
The integer is divisible by 2 twice
OR
the last two digits are divisible by 4
e. g. 25,782 = 82 / 4; not an integer
e. g. 25,756 = 56 / 4; yes
Note:
- Of all quadrilaterals with a giver area, the square has the minimum perimter
When can Smart Numbers be used to solve a problem?
When there are no concrete values in the problem and the answer choices are all variables
- If picking for more than one variable, pick different numbers for each on. If possible, pick numbers with different characteristics (even, odd)
- Follow any constraints given in the problem (positive numbers, or even, or odd)
- Avoid choosing 0, 1, or numbers that appear in the problem
- Choose numbers that work easily in the problem. 100 is often best to use for percent problems
Averages formula
Write the average formula at the top of the sheet when dealing with an Average
- Average = Sum / (# of terms)
Use an average chart for 2+ averages
Even +/- Even =
Odd +/- Odd =
Even +/- Odd =
Even +/- Even = Even*
Odd +/- Odd = Even*
Even +/- Odd = Odd
* When they are the same, Even, otherwise Odd
What is true of exterior angles of a triangle related to interior angles?
Int. A + Int. B = Ext. C
What is the area of a Rhombus?
What is true of the bisectors?
A = (Diagonal1 x Diagonal2) / 2
Diagonals of a rhombus are always perpendicular bisectors
Teeter-totter method or algabraic method:
P is 10% sugar, B is 2%. To make a mixuture of 4%, what ratio of P to B is needed?
Question Asking → P:B
10%P + 2%B = 4%(P+B)
10P + 2B = 4P + 4B
6P = 2B
3P = B
1 P : 3 B
Unknown Multiplier and Ratio Chart
The ratio of lemon juice to wine to water is 2:5:7. If all thee yield 35 mL, how much water was included?
Lemon + Wine + Water = Total
2x + 5x + 7x = 14x –> (2+5+7)
14x = 35
x = 2.5
5 (2.5) = 12.5 mL
*Use a ratio chart when there are 3 or more items
Name the first 10 prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
An integer is divisible by
2 if:
The integer is even
Note:
Be on the lookout for relative values to a total in Data Sufficiency question.
i.e. what fraction of the total pies sold last month were apple pies?
Rephrase the question: a / (a + c) = ?
DS1) the company sold 460 pies last month
a / (460) = ?; not sufficient
DS2) the compnay sold 30% more cherry pies than apple pies last month
1.3a = c
a / (a + 1.3a) = 1 / 2.3; sufficient
Fractions raised to Even vs. Odd Powers
What is true of the area of similar triangles with corresponding side lengths A and B?
If two similar triangles have corresponding side lengths in ratio a:b, then their areas will be in ratio a2:b2
