Quantitative Methods 2 Flashcards
Discrete random variable
Number of possible outcomes can be counted
Continuous random variable
Cannot describe the possible outcomes, as there are an infinite number of possibilities
Binomial distribution - Bernoulli experiment
Bernoulli and binomial variances
Multivariate distribution
Specifies probabilities for a group of related random variables. If returns are modelled as a group, need to take into account statistical interrelationships
Standard normal random variable, Z (descriptive)
- Subtract mean of population from random variable.
- Divide the result by the standard deviation
Standard normal variable formula
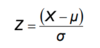
Z table example
Confidence interval
How to use z table for confidence intervals
Use normal distribution and z tables in reverse
Roy’s safety-first criterion
Risk portfolio value will fall bellow a minimum acceptable level
SFRatio
Lognormal distribution
Distribution of the natural log of a normally distributed variable. Bounded below by zero, skewed to the right. Asset prices bounded by zero
Normal/Lognormal distribution
Continuously compounded rate of return
Value at risk
Estimates how much a set of investments might lose given normal market conditions
Sampling issues
When your sample size is 30 or above, you have enough to count as statistically ‘large’
Central limit theorem
Distribution of sample means (DOSM) is approximately normal if the sample size chosen has to least 30 observations
Standard error (s.d. of sampling distribution of the statistics)
Confidence interval
T distribution
Used if population’s standard devision is not known. DOSM is t-distributed not normally disributed
T distribution graphical representation
Sample selection bias
Data availability leads to certain assets being excluded from the analysis
Look-ahead bias
Using information not available on the test date
Time-period bias
Short time periods are likely to give results that may not reflect a longer time period
Long time periods are distortive if there has been structural change
Formal steps in hypothesis testing
- State the null hypothesis and the alternative hypothesis
- Identify the appropriate test statistic and its probability distribution
- Soecify the significance level
- State the decision rule
- Collect the data and calculate the test statistic
- Make the statistical decision
- Make the economic or investment decision
T statistic
Summary of rejection points
Type II error
ACCepting afalse null hyopthesis (beta)
Type I error
Rejecting a true null hypothesis
Standard error population between means
Test statistic population between means
Pooled variance
Hypothesis tests concerning variances
Testing equality of two variances
Using sample variances to determine whether population variances are the same.
Calculate the ratio between the two variances and look up in F-table using n-1 for denominator and numerator.
F-statistic should always be greater than 1
Correlation and regression
