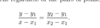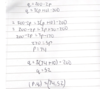Revision of Basic Maths and Linear equations, straight lines and linear inequalities ( Week 1 and 2) Flashcards
We are now going to learn some indices rules?
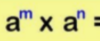
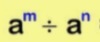
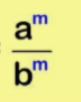
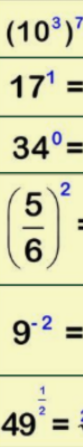
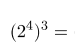
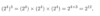
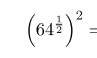
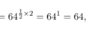
Suppose you eat your house with gas for d days a year and on each day you use m cubic metres of gas. If gas costs £P per cubic metre. Suppose you also have to pay a fixed amount per year £81 per year to the gas company. Suppose that you pay gas bill in twelve monthly installements, write an expression for this?
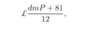
Suppose you eat your house with gas for d days a year and on each day you use m cubic metres of gas. If gas costs £P per cubic metre. Suppose you also have to pay a fixed amount per year £81 per year to the gas company. Suppose that you pay gas bill in twelve monthly installements,
When solving inequalities and we divide by a negative what must we always do?
We must reverse the direction of the inequality
Start by subtracting 6x on both sides?
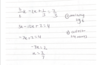
Express this expression in the simplest form?
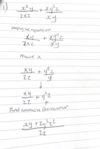
TBA
TBA
TBA
TBA
With a linear equation of one variable ax = c
What happens when A is not = 0
What happens when A = 0
What hapens when C = 0
Draw the lines X = 2 and y=3
What is the form of a linear straight line?
ax+by = c
How do we find the x and y intercepts of a straight line?
We know ax + by = c
The x intercept is when y = 0 this will mean we will have ax = c
x = c/a, so the x intercept coordinate is ( c/a , 0)
The y intercept is when x = 0, this will mean we will have by = c
y = c/b, so the y intercept coordinate is ( 0, c/b)
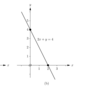
Say we have a line 2x + y = 4, find the x and y intercepts and draw the line?
Lets say we are given a gradient and a point on a line what is the equation of the line using the gradient formula.
e.g. the gradient is 10 and the coordinates are (2,3)
How can we find gradient of a line given 2 points?
If we have the coordinates (1,-7) and (2,3) are on the line, find the equation of the line?
Find the equation of the line given these 2 points
(-2,3) and (4,6) ( do it your way)
Breakeven point is when profit is = 0 for i breakeven point is when x = 5 and for ii breakeven point is then x = 6
Part A
Part B
I DONT NEED TO DO THE TABLE OF X AND Y AS WE SKETCH
a) Consider the line 2x+Y<4 draw the line of a xy plane and shade this region?
b) Then shade the region 2x+y>4
Both are greater/less or equal to
What is one useful economic application of simultaneous equations?
Linear programming, this is where a quanitity is determined by a linear expression e.g ax + by, we can use to find the optimum bundle given the money avaliable.
When doing economic applications, can we have bundles that are negative?
No it doesnt make any sense.
Lets say we want to buy apples and organces but we have a budget constraint what is the expression
x + y = T
How can we find the maximum value of T i.e the bundles of goods he can afford given budget?
Lets say we he X bananans and Y organes and a maxium of 4 pounds to spend find the bundle that satisfies this?
We draw the Budget set ‘bricked region’ and draw the lines T = x+y with T= 1,2,3,4,5,6, we can rewrite y=-x+T, where T is the y intercept, so we need to find the largest T, that is affordable
Notice T = X+Y for T = 1,2,3 is drawn with dashed line, T =4 with a solid line and T>4 dotted line
Lets say for example Jane has a budget set 2x+y =4 and Ashley has a budget set x + 2y =4, how can we find a bundle that simuntaneously maxmises there ultitiy.
