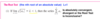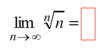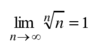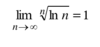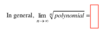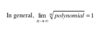Series and Tests for Series

Question 1

Telescoping Series: Use definition (2) to see if a telescoping series converges or diverges.

Answer 1

Expand S_n , collapse the terms, and take the limit as n→∞

If the limit exists, then the series converges to this limit.

If the limit does not exist, the series diverges.

Question 2

Answer 2

Question 3

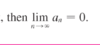
The converse of Theorem 6

Answer 3

Question 4

Answer 4

Question 5

Answer 5

Question 6

Answer 6

Question 7

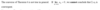
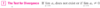
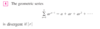
Does a Harmonic Series Converge or Diverge?

Answer 7

Question 8

Answer 8

Question 9

Answer 9

Question 10

Answer 10

Question 11

Answer 11

Question 12

Answer 12

Question 13

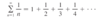
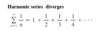
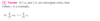
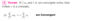
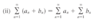
1 / increasing function is

Answer 13

a decreasing function

Question 14

The second method to prove a function is decreasing?

Answer 14

Show f’ (x) <0 eventually

Question 15

Answer 15

Question 16

Answer 16

Question 17

Answer 17

Question 18

A Useful Comparison for

n >3

is?

Answer 18

ln n >1

Question 19

A Useful Comparison for a>0

is?

Answer 19

ln n < n^a

Question 20

A Useful Comparison for

e ^1/<em>n</em>

Is it is between?

Answer 20

1< e ^{1/<em>n </em>}< e

Question 21

A Useful Comparisons for tan^-1

is it falls between

Answer 21

0-1 n < ∏/2 <2

Question 22

A Useful Comparison for sin² x is it falls between?

Answer 22

0< sin² x < 1

Question 23

A Useful Comparisons for cos²x

is it falls between?

Answer 23

0 < cos²x < 1

Question 24

Answer 24

Question 25

Answer 25

Question 26

Answer 26

Question 27

Answer 27

Question 28

Answer 28

Question 29

Answer 29

Question 30

What is the 3 Step procedure when asked if a series is absolutely convergent, conditionally convergent, or diverges?

Answer 30

Step 1: Divergence test in your head on the positive part.

If the positive terms do not → 0, the series diverges by the DIVERGENCE TEST Stop.

If the terms → 0,, move to Step 2.

• *Step 2**: Check absolute convergence. If the series converges, it converges absolutely (and hence converges) and you are done. If no, move to Step 3.
• *Step 3**: Check for Conditional Convergence (with the alternating series test). If the series converges but not absolutely, then the series is conditionally convergent. We do not have any other resource in this course for non-positive series, so you must be given an alternating series if you have arrived at Step 3.

Question 31

Answer 31

Question 32

Answer 32

Question 33

Answer 33

Question 34

Answer 34

Question 35

Answer 35

Question 36

Answer 36

Question 37

Answer 37

Question 38

Answer 38

Question 39

Answer 39

Question 40

Answer 40