SWE Flashcards
SWE: What does it mean for function f(n) to be big-O of g(n), or f(n) in O(g(n)), or f(n) = O(g(n))
There exists number n* and constant c so for all n > n*,
f(n) < cg(n)
SWE: At a high level, what does it mean for f(x) to be big-Omega of g(x)?
It means g(x) is big-O of f(x); it reverses the relationship.
What type of bound does big-O provide on the runtime of our algorithm? What about big-Omega? What about big-Theta?
Big-O provides an upper bound
Big-Omega provides a lower bound
Big-Theta provides both an upper and lower bound, or a tight bound
SWE: What does it mean for f(n) to be big-Theta of g(n)
f(n) is both big-O of g(n) and big-Omega of g(n)
SWE: When we use big-O, are we typically describing best-case, worst-case, or expected-case run time?
Worst case. (But it can be used for the other two.)
SWE: What does asymptotic analysis do for function f(n)? What is our primary tool for asymptotic analysis?
It describes the limiting behavior for function f(n). We use big-O.
SWE: If we have two arrays with lengths a and b respectively, what is big-O run time for nested loops iterating through all elements of one array for all elements of another?
O(ab)
SWE: What are the two main rules for calculating big-O of a function f(n)?
Drop any constants, either multiplicative or additive, and drop any additive terms that are asymptotically not the largest.
SWE: What is big-O of f(n) = 4*2n + 3n10 + 10?
O(2n)
SWE: What “general pattern” emerges for O(log n) runtimes?
Continually dividing n by some constant, such as 2, until you reach 1. (Or, continually multiplying a constant by another constant until you reach n.)
SWE: Why can string questions be approached as array questions, and vice versa?
Because a string is just an array of characters.
SWE: What is a (singly) linked list?
A list of nodes, where each node has a value and a pointer to the next node.
SWE: What is a double linked list?
A list of nodes, where each node has a value and a pointer to both the previous and next node.
SWE: What is an advantage of linked lists over traditional arrays? What is a disadvantage?
Advantage: You can add and remove elements from the end of the list in constant time (whereas with a resizable array, additions are only amortized constant time)
Disadvantage: You can no longer use an index to find a value in constant time. If you want the kth element, you must iterate through k nodes.
SWE: In a linked list, what is a null node, and what is is used for? (In 122’s particular implementation, which I’ll use)
It is a note with a null data value and a null pointer to the next node. It serves as the end of the linked list, or the final node. When iterate throught he list and find a null node, we know the list is over.
SWE: In a linked list, what is a root node?
The root node is the current first node.
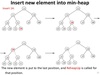
SWE: How would we draw a 2 element linked list, where we have 3 nodes: a root node, a normal node, and our null node?
SWE: When we add a node to a linked list, and the linked list is drawn in our typical way, do we add the node to the left or the right? Why?
The left!
SWE: How do we add a new node to a linked list?
Set the new node to be the root node, and set the pointer of the new node to go to the old root node.
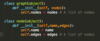
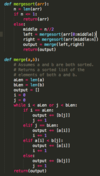
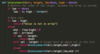
SWE: How do you implement a linked list in python, with add and remove methods?
SWE: Are linked list problems commonly recursive or iterative?
Recursive, because linked lists have a naturally recursive structure. (But there are many problems with iterative solutions too!)
SWE: What is the runner technique for linked lists?
You examine the linked list using two pointers: one that is “slow”, and one that is “fast” and is generally at a farther position in the linked list, and which moves faster than the other.
This is a pretty general technique, but be aware that it exists: examining with two pointers might be handy for many problems.
SWE: What is a hash table used for, and what makes it so useful?
A hash table is a data structure that maps keys to values; you insert key-value pairs, and then search for a key to get its value.
It is useful because it enables fast lookup of elements, in basically constant time as long as your hash table has enough available memory.
SWE: What Python data structure implements the hash table?
Dictionaries (or defaultdicts, which are convenient)
SWE: How is a hash table implemented? What components are needed, and how are they used to insert a key-value pair, or retrieve a key-value pair? (There are multiple possible implementation strategies, we just focus on one in particular.)
Our hash table is an array of linked lists. So each entry in the array is its own linked list.
We use a hash function to map keys to an entry in the array, and this mapping is used for both insertion and retrieval.
To insert pair (key,val), get your hash value h(key), and then find your array index using h(key)%m, where m is the length of the array. We use modulus to keep the index within bounds. We then add our (key,value) pair to the linked list: if the key is already there, we update the value; otherwise, we add a new node with that key-value pair.
To check the value for a key, we get our index h(key)%m again, and look for our key in the linked list at that index. If it isn’t there, then that key hasn’t been inserted.
SWE: What is a hash function? What in general makes a “good” hash function in the context of, say, a hash table?
A hash function maps some value to an integer, in a non-random way. A good hash function will “evenly distribute” values across the different integers. In the context of a hash table, it should distribute the integers evenly across each of the cells of the array. This is good because it leads to fewer long chains in the hash table.
SWE: When making a hash table, why do we need a linked list in every cell? Why can’t we just insert key-value pairs into the cell directly?
Because of collisions: if 2 pairs are mapped to the same cell, they collide, and we can’t put them both in the same cell. Hence, a linked list is used.
SWE: When discussing hash tables, what is a load factor? What does it describe
The load factor is the number of keys in the hash table divided by the length of the array. It is n/m.
It describes how “full” the array is, or how long on average the chains are: if you have a load factor well over 1, then you have several collisions and longer chains.
SWE: What is the worst-case runtime for a lookup in a hash table, in terms of the number of keys n? In what sorts of situations would this happen, and how do these situations cause this runtime?
The worst-case runtime is O(n). This would happen if your array isn’t large enough, and as a result you have some long chains in some of the array indexes.
When looking for a key in a chain, it is O(k), where k is the number of keys in the chain. If you have a lot of keys in the chain – an amount that becomes substantively “on the order of” n, such as say n/10, then you’re looking at linear time.
SWE: When using a hash table, how can we assure constant-time insertion and lookups?
You need to keep your load factor low; you need to have a large enough array so there are few collisions, leading to chains that are at most a few elements long.
SWE: Hash tables are typically used for storing (key,value) pairs, but what is an intuitive way to have them store just keys? So like a set in python rather than a dictionary?
In traditional hash tables, you hash the key, then insert the key-value pair at the corresponding location. But there’s no reason you need a value: you could just insert the key.
(If you have a hash table set up like a dictionary, you could also just give every key a value of NULL which you ignore.)
(This is pretty simple, but I want to remember you can also easily make a hash table that works like a set!)
SWE: Is a stack first-in-first-out or first-in-last-out? Is a queue first-in-first-out or first-in-last-out?
A stack is first-in-last-out
A queue is first-in-first-out
SWE: What is a stack? How is it used at a high level?
A stack is a data structure which stores elements. You can add an element (or “push” it), and you can remove an element (or “pop” it). Elements are removed in reverse order of how they’re added, or first-it-last-out. This is like a stack of blocks where you continually add a blocks to the top when you want to add, and remove a blocks from the top when you want to remove.
SWE: How do you simply implement a stack – with pop, push, peek and isEmpty methods – if you already have an implementation of another key data structure?
You need a linked list implementation. Recall that a linked list has a null node as the “final node” on the right with no descendants, and the “first node” being the root node which has nothing pointing to it. To add an element to the linked list, you make it the root and make the old root its descendant. To remove an element, you make its descendant the root.
In other words, a linked list is basically already an implementation of a stack. To push, you just add the value to the LL. To pop, you just remove the root from the LL. To peek, you just look at the value in the root of the LL. To check if it’s empty, you see if the root node is the null node.
SWE: What is a queue? How is it used at a high level?
A queue is a data structure which stores elements. You can add an element (or “push” it), and you can remove an element (or “pop” it). Elements are removed the same order as how they’re added, or first-it-first-out. This is like a queue of people who are waiting in line, where the first person to get in line is the first person to get out.
SWE: How do we implement a queue, with push, pop, peek, and isEmpty, using another common data structure?
We will implement the queue using a slight variation of a linked list.
With a normal linked list, the list is visualized several nodes with arrows pointing left to right. On the far left is the root node; the linked list data structure keeps track of the root node, and a newly inserted value enters on the left and becomes the new root. The linked list also has a null node to the far right.
In a queue, we are going to insert elements on the right side of the linked list, or the back, and we (same as a normal linked list) remove elements from the left side of the linked list, or the front. So the arrows between nodes point from front to back, which may seem unintuitive.
Thus, we now keep track of two nodes rather than just one. We keep track of the front, or the root, as well as the back, which is the last node in the list. The back node doesn’t point to anything; it’s easier in a queue to not have a null node and instead keep an “empty” bool in the data structure. When the queue’s empty, set the front and back pointers to just point to NULL.
To push a value onto the back of the list, we make a new node, have the current back point to it, and set the new node as the back. To pop a value from the list, we set the front’s descendant as the new front. To peek, we return the value at the front. For isEmpty, we check the bool.
SWE: What is a tree?
A tree is a data structure which organizes nodes in terms of parent-child relationships, where each node can have at most one parent, but nodes could have several children.
A tree is basically a DAG, or directed acyclic graph, that is also connected, meaning it’s not like two or more graphs that don’t touch each other.
SWE: In a tree, what is a parent and what is a child?
Simply, if node A is directly above node B, A is the parent of B and B is the child of A
SWE: In a tree, what is an ancestor and what is a descendant?
A descendant of node A is any node you can get to by following branch down from A.
An ancestor of A is any node for which A is a descendant.
SWE: In trees, what is a branch, starting at say node A
A branch is a “path” from start node A down through multiple parent-child relationships, always moving from parent to child, until we reach a leaf node.
SWE: In trees, what is a leaf? What is the root?
A leaf is a tree with no descendants; the root is a tree with no parents.
SWE: Given a tree, what is the subtree with node A as the root?
It’s simply all node A as the root of a tree with all of the descendants. It’s basically the tree you get if you erase anything from the original tree that wasn’t A or a descendant of A.
SWE: What makes a tree binary? What makes a tree ternary?
A binary tree is where each node can have at most two descendants (but only 1 parent). A ternary tree is where each node can have at most three descendants (but only 1 parent). And so on.
SWE: What is a binary search tree?
It’s a binary tree where, for every node n, you have the property that:
All left descendents of n < n < all right descendants of n.
(There can be differing opinions on equality in the tree. Sometimes above will read <= n
SWE: How do you search for an element in a binary search tree? How do you insert a new element into a binary search tree (where it doesn’t necessarily need to be balanced)?
To search for an element x, you follow a branch down the tree using the information that the tree is in a way “sorted”. So if you’re at node y and y < x, you move down the left branch, because x then would definitionally need to be on the left. If x < y, you move down the right branch.
To insert, you do the same thing and move down the tree in this way. If you find x, you typically wouldn’t insert it again. If you find a leaf without finding x, you insert it on the appropriate side of the leaf.
SWE: Why is a binary search tree useful for searching for elements?
Because of the ordering properties of the BST, you only need to search down one branch rather than the whole tree. This means that if the tree is balanced, you can search for an element in only log(n) time.
SWE: What is a complete binary tree?
A complete binary tree has every level fully filled out, except for potentially the last level. If the last level isn’t full, it’s filled in from left to right.
SWE: What is the height of a tree? What is the height of a tree with just a root, or an arbitrary tree?
The height of a tree is the length of its longest branch. Specifically, it’s the number of edges along the longest branch.
We say that just a root node has a height of 0, because the longest path has no edges.
To find the height of an arbitrary tree, just follow all the branches down to their leaves, adding 1 to that branch’s length for each node past the root, and thus for each edge. Take the max branch length as the height.
SWE: What is one way you learned to achieve balanced binary trees?
AVL Trees
SWE: What is the technical definition of a balanced tree? And what is a more colloquial, slightly more relaxed definition of a balanced tree?
Technically, a balanced tree is a tree such that, for every subtree present, the height of its left subtree and its right subtree differ by at most 1.
Colloquially, it’s basically a tree that is balanced “enough” among all subtrees such that we can expect traversals of a single branch to take O(log n) time, rather than linear time.
SWE: How do you implement a tree where each node can have an arbitrary number of descendants? What datatype is necessary, and what datatype is optional but usually not useful for interviews?
Also, how would you adapt this implementation to be specifically a binary tree?
You will need a treeNode class, which has a data attribute holding its value and a descendants attribute which holds a list of its descendants.
You can also include a Tree class, whose only attribute is a root node, but it’s usually not helpful for interviews?
If you want specifically a binary tree, your treeNode class would have three attributes: data, leftDescendant, and rightDescendant.
SWE: What is an in-order traversal of a binary tree? How would you write a function to perform an in-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an in-order traversal, at every node, you explore the left subtree of the node (and visit all of the nodes in that subtree), then visit the node itself, then visit all of the nodes in the right subtree.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:
SWE: What is an pre-order traversal of a binary tree? How would you write a function to perform an pre-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an pre-order traversal, at every node, visit that node, then you explore the left subtree of the node (and visit all of the nodes in that subtree), and then visit all of the nodes in the right subtree.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:
SWE: What is an post-order traversal of a binary tree? How would you write a function to perform an post-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an post-order traversal, at every node, you explore the left subtree of the node (and visit all of the nodes in that subtree), then visit all of the nodes in the right subtree, and then lastly you visit the node itself.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:
SWE: What is a max heap, in the context of a min heap? Why is it very easy to implement a max heap if you understand min heaps?
In a min heap, all nodes’ descendants are larger than the node. For a max heap it’s simply the opposite: all nodes’ descendants are smaller, so the max is at the top. So the implementation is basically the exact same, you just do the orderings in reverse.
SWE: What is a binary min-heap?
A complete binary tree where each node is smaller than its children, so the min of the tree is always at the root.
SWE: How do we insert a new value into a min heap?
A heap must be a complete tree, meaning the bottom layer is filled out from left to right; so, we start by placing our new node in the bottom layer, to the right of the rightmost node in that layer.
Then, we continually swap that new node with its parent, until its parent has a lower value than it. This restores the min heap to its correct form.
SWE: How do we extract the minimum value from a min heap, removing it from the tree?
We first remove the minimum value from the top (it’s always at the top).
A min heap must be a complete tree, so next we take the rightmost node on the bottom layer and place it at the top, where the min value originally was.
Now we need to restore the ordering. We continually look at the node we just moved to the top and its two descendants. If the node we moved is the smallest of those three, we stop. Otherwise, we swap it with whichever of its descendants is the smallest of the three.
SWE: At a high level, what is a trie (or prefix tree), and what is it typically used for?
A trie is a tree with a letter at each node. As you move down a branch, you find a word, or a prefix for a longer word.
Branches sometimes have * values at the leaves to signify the end of a word.
They’re often used for interview problems where you need to look up words, or several words with the same prefix, etc. You can see if a word is present in the trie in O(length of word) time, because you can follow the prefix down the tree.
SWE: How would you implement an adjacency list for a graph in an object-oriented way? How would you implement it just using list data structures?
To do it object-oriented, you could have a Graph class, with objects having a list of nodes as an attribute, as well as a Node class, with objects having a name attribute as well as a ListOfEdges attribute, which is just a list of the nodes into which it has an outgoing edge. The picture shows this implementation.
To do it with just arrays, you could assume your n vertices are indexed from 0 to n-1 and use a 2d list: each entry at position i in the high-level list would be a list of indices j into which i has an outgoing edge.
SWE: What is Depth-First Search, or DFS? How does it work at a high level?
Depth-first search is a way of searching through a graph, to either visit all of its nodes, or to find a specific node. In depth-first search, you move fully down a branch before moving to the next one, hence “depth-first.”
A depth-first search starts at a specific node in the graph; you may be given a specific start node, or it may be arbitrary. You search through each of the node’s neighbors, but you move fully down a branch before moving to the next. You must keep track of all of the nodes you have visited, because if you see a node you’ve already visited while exploring a branch, you don’t visit it again.
SWE: What is some pseudocode for depth-first search?
A recursive approach works best:
SWE: What is Breadth-First Search, or BFS? How does it work at a high level?
Breadth-first search is a way to search through a graph, in order to either traverse all of the nodes, or to find a path from one node to another. You’re given a starting node (or choose one randomly), and then you visit all of its neighbors before visiting any of their neighbors, hence “breadth-first.” You can think of it as moving out from the root layer-by-layer.
SWE: What is some pseudocode for breadth-first search?
We use an iterative solution (unlike DFS, which is recursive) which takes advantage of a queue. The queue stores nodes we need to visit, in the order in which we need to visit them.
We “mark” a node before pushing it onto the queue, and when iterating through a node’s neighbors, we only push it onto the queue if it isn’t marked. This is because we always push a node on after we mark it, so if it’s already market, that means it’s already in the queue, and we don’t want to put it in the queue twice and thus visit it twice.
SWE: How does bubble-sort work at a high-level? Additionally, how do you code bubble-sort in Python?
Bubble sort sorts the elements of a list by continually finding the largest element and moving it to the end of the list. So you find the largest element and put it last; then you find the second-largest element and put it second-last; and so on. You do this by continually passing forward through the list and switching an element with the next element if it’s larger than the next element.
SWE: How does mergesort work at a high level? How do you code it in Python?
You split the array into two halves, sort those halves recursively, and then combine them using a merge() function, which can combine two sorted lists into one sorted list containing the elements from both. Your base case is if a list has length <= 1.
To merge two lists, just continually add the smallest element in either list to a helper list, with pointers in each list keeping track of which elements you’ve already viewed?
SWE: What is the time complexity of mergesort (for an array of length n), and why? What is the space complexity, and why?
The time complexity is O(n log n). Here’s how to think about this: we split the array into singles; then we merge into doubles, then quadruples, etc. In order to merge two lists, we need to traverse both lists. So when combining singles into doubles, we must traverse each single once; when combining doubles into quadruples, we must traverse each double once; and so on.
This means that at every “level”, we need to traverse all the data. And how many levels are there? We merge 1’s, then 2’s, then 4’s…up to n. So log n levels, each traversing the whole dataset of length n, gives O(n log n).
The space complexity is O(n). We need to store temporary arrays to fill with the sorted values, and the max length of one of these arrays is n. We can reuse the same space for each array assuming we are solving the problem with a single processor, and thus only working with a single recursive example each time. Thus, O(n) space.
SWE: How does quicksort work? How does the algorithm work at a high-level? And how do you code it in Python?
It’s recursive: if the length of the list is <= 1, you just return the list.
Otherwise, you pick a “pivot”, which is just any of the elements of the list. You could pick it randomly (preferred), or have some default like always picking the first element in the list.
Then you move through the list, putting each element in one of 3 new lists: less than the pivot, equal to the pivot, and greater than the pivot.
Lastly, you recursively sort the elements on either side of the pivot, then you combine the lists.
SWE: What is the worst-case runtime of quicksort? What is the average-case runtime of quicksort? And why?
The average-case runtime, or the expected runtime, is O(n log n). This is because on average, the element you choose as the pivot will equal about the median of the list. So you split the list into roughly equal parts, then recurse and split the sublists into roughly equal parts, etc. So we now have a setup that looks a lot like mergesort: you have log n levels, and at each level you handle each element in the original list once, giving O(n log n).
The worst-case runtime is O(n2). If you always pick the biggest element in an array as the pivot, for example, then your splits of the list are always uneven, and you sort lists of size n, n-1, n-2… as opposed to n, n/2, n/4….. and this leads to O(n2).
SWE: How do you write binary search in Python?
SWE: In Python, how do I make a class A with attribute x, and a subclass B that has attributes x and y? Both classes should have __init__() functions
SWE: In Python, if we have a class A and a subclass B, how do we override the method g() from class A, so that “g” has a different functionality in subclass B?
Simply redefine g() in subclass B. If you don’t specify a g() when creating subclass B, it’ll use class A’s g(), but if you do specify a g(), then that is what will be used.
SWE: In bit manipulation, given two binary numbers x and y, what are the common symbols for x and y, x or y, x XOR y, and not x?
And: x & y
Or: x | y
XOR: x ^ y
Not: ~x
SWE: How do we find the two’s complement of a binary number K for the purposes of storing -K, and where do we get this definition from? How would this work for the example of representing -3 if you have 4 total bits available to represent numbers?
From various sources “The two’s complement of an N-bit number K is the complement of a number with respect to 2N; it is the number X such that K + X = 2N”
This can be confusing because here, N-bit number doesn’t mean the number of bits needed to represent the number, it’s the number of available bits that the computer uses to store any integer, minus the sign bit. So of your computer is storing 16-bit integers, then one of those is the sign so they’re really 15-bit integers, so the two’s complement of K is X such that K + X = 215.
Lastly, we can quickly calculate the two’s complement of K by flipping all the bits and adding 1.
For example, in the following table, we’re representing values between +7 and -7 as 4-bit numbers, meaning we have 3 bits for the number and 1 for the sign, so here N = 3.
So, say we’re trying to represent -3 in binary. Now K=3, and for K = 3, the two’s complement is X such that 3 + X = 23 = 8.
So the two’s complement of 3 is 5, and thus the representation for -3 is going to be the representation for 5, plus a 1 at the beginning for sign.
To find this, we can either know of the top of our head that 5 is 101, or we can do it by flipping the bits in 3 and adding 1. This is more scalable for when you have lots of digits, and also you can implement it in code.
3, when you have 3 digits to represent it is 011; flipped that’s 100, and adding 1 you get 101, which is 5, the two’s complement. Tacking on a 1 at the beginning for sign, you have 1101, the binary representation of -3.
SWE: What are two ways to think about multiplying numbers in binary; for example, 1001*101
The first is to just use the gradeschool base 10 algorithm, but just in binary. In the base 10 algorithm, you multiply the top number by each of the digits in the bottom number, and you add an extra zero in every row. You do this here, remembering that 1*1 = 1, 1*0 = 0, and 0*0 = 0. There’s no carrying or anything. This is shown in the example below.
But, you can also use this idea that to multiply by a power of two 2N, you can just shift left by N bits. So you can also take each of the digits, which are 2N numbers, do all of those shifts, and then add them up. This is exactly what we’re doing in the grade school algorithm, but a different way of doing it. This is nice because we can recognize tricks quickly and save ourselves work. To multiply 1111111 by 10000010 would take a while, until you realize you need to just do two bit shifts, and add those two results.
SWE: Given a binary number N, how do we get the value of the ith bit? Here the 1’s place is the 0th bit, the 2’s place is the 1st bit, etc.
We first AND N with a string S that is all 0’s except for a 1 in the ith bit; the result will be a string of 0’s with a 1 in the ith bit iff N has a 1 there. (You can generate S by bitshifting 1 to the left until you have S.)
Then, we just compare the result to 0: if it equals 0, then the ith bit was 0, otherwise it was 1.
SWE: How does a MapReduce program work for analyzing data? What does the programmer need to implement, and then how does the computer resolve the MapReduce program?
How does this work on the common example of counting the number of appearances of each word in a dataset of words?
A MapReduce program takes a dataset containing many points (or just a set of objects containing many objects).
It first maps each data point to a pair. Then, it takes all of the pairs with the same key and “reduces them” in some way, emitting a new, single pair.
As a programmer, you just need to implement a map() function and a reduce() function that makes sense for your use case. The reduce function takes only two values, like in 210; it doesn’t take the whole list of values you need to reduce. You reduce a list by continually reducing pairwise, which is what the machine will do. This is important to note in many cases when considering how to implement the reduce.
(It’s often helpful to first think about how to implement the reduce step, and what that needs to be like, and then figure out the map step based on that.)
The computer first splits the data across several machines, or processors. Each processor runs the map() function on each of its points. Then, the computer does an automatic “shuffle” of the pairs, where each pair with the same key is on the same processor. Lastly, each processor reduces the pairs with the same key using the reduce() function.
For the example where we’re counting the number of appearances of a word, we map a word to , and reduce the pairs by summing the 1’s and keeping the word as the key. This is shown visually, executed by the computer, below.
