ML

Question 1

ML: What are loss functions?

Answer 1

Functions that numerically compare your predictions Y* to the true values Y to provide feedback on the accuracy of your trained model.

Question 2

ML: What is the typical loss function for classification? For regression?

Answer 2

Classification: 0/1 loss

Regression: Mean-Squared Error (MSE)

Question 3

ML: What is a generative model?

Answer 3

It models P(Y|X) using P(X|Y)P(Y)

(derived from Bayes rule)

Question 4

ML: What is a discriminative model?

Answer 4

Models P(Y|X) directly, as P(Y|X)

Question 5

ML: What are some advantages of discriminative model over generative? What about generative over discriminative?

Answer 5

Discriminative models (Y|X) don’t need to make assumptions about the distribution of X|Y, and can be simpler as a result.

Generative models can be used to generate samples. They are also sometimes more intuitive.

Question 6

ML: What is a Bayes classifier?

Answer 6

Question 7

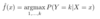
ML: What are 2 important characteristics of a Bayes classifier?

Answer 7

It is the best possible classifier

Its error is thus the irreducible error of a classification problem.

Question 8

ML: At a high level, how would a Bayes Classifier be constructed in a case where errors are asymmetric, meaning some errors are worse than others?

Answer 8

We would weight each possible error with its own amount of loss L_i,j, pertaining to what you said the answer is and what the answer should’ve been.

Question 9

ML: What is a simplistic view of logistic regression when Y is binary?

Answer 9

We are just doing a linear regression on our X’s, then squishing the outcome into [0,1]

Question 10

ML: In binary logistic regression, what is the formula for P(Y=1|X=x)?

Answer 10

For x of any dimension, it is as follows:

Question 11

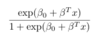
ML: What is the formula for the logit^-1 function, or the inverse logit function? And what does it accomplish?

Answer 11

It is shown below. It squishes all real numbers x into a range of [0,1]

Question 13

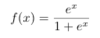
ML: In binary logistic regression, given the formula for P(Y=1|X=x), how do we choose our predicted outcome?

Answer 13

We of course simply choose the outcome with the higher probability.

Question 14

ML: What is the final decision rule for logistic regression in its simplest form?

Answer 14

Question 15

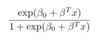
ML: What decision boundary does binary logistic regression yield?

Answer 15

It yields the linear separator:

Question 16

ML: For binary logistic regression, how do we learn the coefficients of the model B₀, B₁, B₂… in order to make predictions?

Answer 16

We estimate them using simple maximum likelihood. So we find the coefficients B₀, B₁, B₂… that have the highest likelihood of producing the observed training data with the observed labels.

However, this optimization function using 0/1 loss is computationally hard, so we solve it iteratively using something like stochastic gradient descent.

Question 17

ML: How to we extend binary logistic regression to multinomial logistic regression? So our X’s are still n-dimensional vectors, but now our Y’s are scalars in [1,K]?

Answer 17

Question 18

ML: What issue arises when logistic regression is performed on data that is perfectly linearly separable? And how can we combat this?

Answer 18

The learned weights will go to infinity, and we will overfit.

We can combat this by regularizing!

Question 19

ML: What does having a high number of parameters in your model do to the bias/variance tradeoff?

Answer 19

Having a lot of parameters, or a complex model, decreases bias (as we have more flexibility to fit whatever truly is the underlying model) but variance increases

Question 20

ML: What does having a high number of features in your model do to the bias/variance tradeoff?

Answer 20

Having a lot of featuers decreases bias (as we are able to fit more of the possible underlying models), but variance increases due to the curse of dimensionality.

Question 21

ML: In general, what kinds of changes to your model will decrease bias, but increase variance?

Answer 21

When you allow your algorithm the potential ability to fit a higher amount of potential underlying models, or more types of underlying models.

This of course decreases bias as you are more likely to hit the real model, but it increases variance because (I think) when you have more possible options and the same amount of data, it becomes more likely that one of them appears as the best-fitting model due simply to noise.

Question 22

ML: In general, what sorts of changes to your algorithm will decrease variance, but increase bias?

Answer 22

Changes that make your algorithm less influenced by outliers or noise.

Question 23

ML: What is a definition of model bias that is useful to think about when considering the bias/variance tradeoff?

Answer 23

Bias in a model is a lack of ability to fit the underlying model.

In other words, a lack of robustness with which to fit potential underlying models

Question 24

ML: What is a definition of model variance that is useful to think about when considering the bias/variance tradeoff?

Answer 24

Model variance is its amount of susceptibility to changes due to noise.

Question 25

ML: What is the naive bayes assumption, both in words and mathematically?

Answer 25

In words, the naive bayes assumption is that there are no interactions between the features of n-dimensional feature vector X, or that the context of one of the features X_i, and how it interacts with other features X_j, is not relevant to prediction.

(An example is assuming seeing “Donald Trump” is has the same predictive value as seeing those two words 10 words apart and in reverse order.)

Mathematically, we have for D-dimensional X:

Question 26

ML: Is Naive Bayes a discriminative or generative model?

Answer 26

Generative

Question 27

ML: What is the form of P(Y=y|X=x) under the Naive Bayes classification algorithm?

Answer 27

P

Question 28

ML: How do we learn a Naive Bayes classifier? What parameters need to be estimated, and what options do we have to estimate them?

Answer 28

For each Y=y, we need to estimate P(Y=y), as well as P(X_i=x_i|Y=y) for every possible value of X_i.

P(Y=y) is generally estimated through MLE. So, we just estimate it as the proportion of the training examples for which Y=y.

For P(X_i=x_i|Y=y) it can vary. You could also do basic population MLE (The proportion of X_i=x_i among training examples where Y=y), or you could learn a gaussian N(µ,σ²) as with gaussian naive bayes, or something else!

Question 29

ML: What are the advantages and disadvantages of Naive Bayes?

Answer 29

The disadvantage is that we cannot capture context, which is often very important. Hence this algorithm being “naive”.

The advantage is that it’s simple, and is much easier to train: because we ignore interactions, we only need to learn a bunch of univariate distributions rather than one giant joint distribution, which is much harder (I believe exponentially harder).

Question 30

ML: What do the decision boundaries look like in multinomial logistic regression?

Answer 30

We’re finding n linear (or hyperplane) separators, one for each of the K possible Y=k which models P(Y=k) vs P(Y not k). As such, it looks like a bunch of k linear (or hyperplane) separators working together on the cartesian grid.

Question 31

ML: What is the most common way to train a decision tree, without yet worrying about pruning?

Answer 31

At each step, simply greedily add the split that most decreases classification error on the training set (or MSE in the case of regression).

Question 33

ML: What is the common way to validate a decision tree and combat overfitting?

Answer 33

Pruning. Once you have your full tree trained on training data, at each step, greedily remove the branch that causes the largest improvement on validation error. Continue until you can’t find any more improvements to validation error.

Question 34

ML: How do we predict on a new point X using a trained decision tree, for both classification and regression?

Answer 34

Simply work your way a branch until you get to the bottom. For classification, return the most common label among the training examples at that branch. For regression, return the average training label.

Question 35

ML: What is the main advantage of decision trees? (Not in ensembles or anything, just by themselves.)

Answer 35

They’re very interpretable, especially to non-technical people

Question 36

ML: What sre some disadvantages of decision trees? (Not in ensembles or anything, just by themselves.)

Answer 36

They don’t predict very well.

Variance is very high, as small changes in training data can cause big differences in how the splits occur.

They also have a fair amount of bias, as they can only capture certain types of decision bounds (no “diagonal” decision bounds).

They also handle categorical predictor variables poorly if there are too many predictors.

Question 37

ML: What issue do decision trees have with categorical predictor variables?

Answer 37

If the variable has N possible valuest each split, it must consider each of the 2^N-1 subsets of the values as a splitting rule, which is of course very computationally hard.

Question 38

ML: As the depth of a decision tree grows, what happens to bias and variance?

Answer 38

Bias decreases (as we increase complexity), and variance increases.

Question 39

ML: How do ensemble classifiers generally work?

Answer 39

Several models are learned, and they vote on what the prediction is.

Question 40

ML: What is boosting? How does it generally work?

Answer 40

In boosting, you fit several (typically very basic) classifiers iteratively, with each new classifier trying to do well on the training points that the previous classifiers did poorly on.

Question 41

ML: How does boosting improve the performance of the classifiers its using? In otherwords, how does bias and/or variance impacted before and after the use of boosting?

Answer 41

Because it uses very simple predictors (for example, stumps of decision trees), each one individually has very high bias. But, by fitting a lot of them and correcting for previous mistakes, bias is decreased.

Question 42

ML: How does prediction work for a KNN classifier or regressor?

Answer 42

For each new point, you find the K points in the training set closest to it (by some measure such as euclidean distance); then for classification you’d return the most common label among the nearest neighbors, and for regression you’d return the average label of the nearest neighbors.

Question 43

ML: What is the (somewhat high-level) algorithm for Adaboost?

Answer 43

We start with each training example X_i having equal weights w_i. Then, repeat:

1. Fit a new classifier that minimizes weighted training error, based on the weights w_i. (Points on which earlier classifiers have performed poorly have higher weights, and errors on those points cost more)
2. Based on the weighted error of that classifier, find a weight alpha_j for the classifier for when it votes later on. The lower its weighted error, the higher its alpha_j, and thus the higher its voting power.
3. Update each of the point weights w_i based on this round’s results.

Question 44

ML: How (at a high level) does gradient boosting work?

Answer 44

At each step, we find the current gradient of the loss function. We then find our next classifier to “approximate this gradient vector”.

So we in some way optimally take into account the gradient of the loss function at each step as we choose our classifiers.

Question 45

ML: What issue do we run into when trying to minimize 0/1 loss for our classification problems? How can we solve this issue?

Answer 45

Because the 0/1 loss function is not smooth, as well as nonconvex, optimizing the solution is very hard, and you also can’t approximate it with iterative techniques like gradient descent (which is generally the solution when finding the true global minimum is impossible).

To combat this, you can instead iteratively minimize some similar loss function that puts an upper bound on 0/1 loss, such as hinge loss (pink), or exponential loss (yellow).

Question 46

ML: How does bagging work, at a fairly high level? How do we train a baggng ensemble given a training set of n X_i’s?

Answer 46

Resample several samples from your training data; say m bootstrapped samples of size n, with replacement.

Train a (typically complex) model on each of the m bootstrapped samples. Have these models vote on the prediction.

Question 47

ML: How do bias and variance work with bagging? So what is the level bias and variance from one of the individual classifiers in the ensemble, and then what happens to bias and variance when we have several classifiers vote?

Answer 47

The classifiers in bagging are complex; if they’re trees, they’re deep trees. As a result, the individual classifiers have low bias, but high variance.

However, when we use several classifiers and have them vote, we can drive down this variance because we’re averaging votes from classifiers trained on different bootstrapped samples. (As n goes infinity, these samples become independent.)

Question 48

ML: What are the high-level differences between boosting and bagging, and how they achieve the goal of making several classifiers work effectively together?

Answer 48

Boosting fits several models that are not complex, and thus have high bias. But by fitting several and correcting errors from previous iterations, bias is reduced.

Bagging fits several complex models, so bias is lower but variance is high. But by averaging many predictions on slightly different datasets, we can lower variance.

Question 49

ML: What is an improvement we can make to bagging (specifically classification bagging) when we are calculating our predicted class?

Answer 49

Rather than just picking the class with the most votes from each of the classifiers, average the probabilities of each class from each of the classifiers, then predict the class with the highest probability.

(If we get to the end of a branch in one of the classifiers, the “probability” of class j predicted by that classifier is the proportion of training examples that had class j).

This improvement makes performance more consistent, decreasing variance a bit.

Question 50

ML: How do Random Forests work?

Answer 50

Random Forests work basically just by using bagging with deep decision trees: bootstrapping several resampled training sets, training a deep tree on each of them, and having them vote for a classification or regressed value.

The key change from traditional bagging is this: if there are p features of a training example X, at each split in a decision tree, only m < p features are considered for that split. (Typically m = sqrt(p))

Question 51

ML: Why is the Random Forest alteration to bagging often advantageous?

Answer 51

By only considering m < p features at each split of a decision tree, the trees become more independent, which helps the random forest algorithm decrease the variance in the overall prediction (which is the general goal of bagging).

Question 52

ML: What are two cons of bagging/random forests?

Answer 52

The models lack interpretibility.

Training and prediction both take a long time.

Question 53

ML: What method is typically used to evaluate random forests instead of cross-validated error? Why is this other approach typically better for random forests?

Answer 53

You use out-of-bag error. Because each classifier is trained on a bootstrapped training set, each point in the original training set was not used in training some of the classifiers (about 36.8%). So, get a prediction on this point from these classifiers, and find the error on all the points from that method.

This is preferable to cross-validation because you don’t need to retrain the model for each of the folds; training takes a long time for random forests, so we want to avoid it. But with enough trees, out-of-bag error tends to be very similar to CV error.

Question 54

ML: What do variable-importance measures look at? On which algorithm are they most often used and why?

Answer 54

Variable-importance measures look at how important a variable is to the predictions of the model.

They’re commonly used for random forests, because random forests lack interpretability without them.

And more recently in my experience, they’re big for xgboost. Ensemble tree methods just lend themselves to variable importance metrics, because you can look at how often a tree chooses to split on a given variable, how the model performs with and without trees that use a certain variable, etc.

Question 55

ML: For random forests, what are the 2 most common ways to calculate variable importance metrics?

Answer 55

1. Find all of the splits which use that variable in all of the decision trees, and then find how much on average those splits improve the predictions, using some measure of prediction performance like Gini index.
2. Randomly permute each variable one at a time, and see how much model performance decreases for each. (I’m guessing this means to calculate out-of-bag error, and for each point, before getting the prediction, choose the value of the variable in question randomly.)

Question 56

ML: What is clustering, and how does it differ from classification?

Answer 56

Clustering is an unsupervised learning technique, so our training data are not labeled, and we try to divide the data into groups that are in some way “similar”. So basically, we try to label each point such that similar points have the same label.

Classification is similar because each point has a label, but classification is supervised: we are given a labeling scheme and want to learn how to predict it as best as possible. With clustering, we aren’t given a labeling scheme, and want to find a sensible one.

Question 57

ML: What does k-means clustering approximately minimize? And how does its approximation of this minimization work on a theory level?

Answer 57

Question 58

ML: How do you run the k-means clustering algorithm?

Answer 58

After choosing your number of classes k, randomly initialize the locations of your k cluster centers. Then, repeat:

1. Assign all training points to the cluster center that is closest by euclidean distance
2. Set cluster center as the average of all points in the cluster

Question 59

ML: What are some drawbacks to k-means clustering?

Answer 59

1. It’s nondeterministic due to the random initializations, and is not guarenteed to reach the global optimum.
2. Cluster center isn’t interpretable, as it’s an average of a bunch of points

Question 60

ML: What is an advantage to k-means clustering?

Answer 60

It will always converge, as each step will decrease the in-cluster variance (until it’s at a local minimum)

Question 61

ML: How does the k-medoids algorithm work? Specifically, what alterations are made to the k-means algorithm?

Answer 61

Here the cluster centers are actual points in the dataset, rather than an average of a bunch of points.

So we initialize k points randomly to be the initial cluster centers, then repeat:

1. Assign all training points to the cluster center (a real point) that is closest to it
2. For each cluster, choose the point in the cluster which minimizes mean squared distance from other points as the new cluster center. (In other words, minimize in-cluster variation.)

Question 62

ML: What is a pro of k-medoids over k-means? What is a con?

Answer 62

K-medoids provides more interpretable cluster centers, as they are actual points in the dataset rather than an average.

However, this is at the cost of having slightly higher in-cluster variation for k-medoids, as you simply have “fewer choices” of where to put your cluster center.

Question 63

ML: At a high level (so for an arbitrary linkage), how does the hierarchical clustering algorithm work?

Answer 63

Each training point starts as its own cluster. Then at each step, we merge the 2 clusters with the highest similarity into one. We use linkages to determine similarity.

Question 64

ML: In hierarchical clustering, what are 4 common linkage options for determining similarity of 2 clusters?

Answer 64

1. Single linkage: Dissimilarity between 2 clusters is the distance between the two points closest to one another across groups
2. Complete linkage: Dissimilarity is the distance between the two points farthest to one another across groups
3. Average linkage: Dissimilarity is the average distance across all pairs of points between groups
   4: Centroid linkage: Dissimilarity is the distance between the averages of the points in each group

Question 65

ML: What are a few advantages to hierarchical clustering?

Answer 65

1. It is deterministic, and thus has lower variance
2. You get clusterings for all values of k
3. You have hierarchical clusters! If your clusters naturally have a sub-cluster architecture, this is useful.

Question 66

ML: At a very high level, how do mixture models work?

Answer 66

When looking at our training data, we assume they come from a probability distribution that is a weighted sum of several simple underlying distributions, such as several gaussians.

Question 68

ML: What advantage do mixture models have for clustering?

Answer 68

Rather than having each point discretely in one cluster, we compute the probability that each point is in each cluster. This is good for overlapping clusters, or for clusterings where some points have an unclear affiliation.

Question 69

ML: At a high level, how are mixture models used to produce a clustering, and to determine the clustering of a new point?

Answer 69

To produce a clustering from training data, we learn the parameters of the k underlying simple distributions (using a technique called expectation maximization) that we think may be forming the overall distribution.

To “assign each point to a cluster”, we compute the likelihood that each of the simple distributions would have produced this point. Here each simple distribution acts as a cluster, with a center at the simple distribution’s mean, and we see probabilistically from which cluster the point was likely to come from. We thus don’t have a “hard clustering”

Question 70

ML: For the purpose of clustering using graphs, what are 3 ways to compute a graph from training data?

Answer 70

1. Connect 2 points iff their distance is below a threshold epsilon (epsilon-nearest-neighbors)
2. Connect 2 points iff one is a KNN of the other, for some k
3. Form a weighted graph where points with close euclidean distances have high weights

Question 71

ML: What is a graph cut? For the purposes of graph clustering, what 2 propert do we want a cut to have?

Answer 71

A graph cut is simply putting the vertices into 2 (or more) subsets, but it can be visualized as “cutting” across the edges which go between your two subsets.

We want our cuts to :

1. Have a low total weight of cut edges. So if we’re using an unweighted graph, we want to cut as few edges as possible; if the graph is weighted, we want to cut as little weight as possible. This increases dissimilarity across clusters and similarity within clusters, as edges are drawn between similar points
2. We want cuts to be balanced (or approximately balanced), meaning that a similar number of points is in each subset. This avoids putting one point in a subset, for example.

Question 72

ML: What is a key advantage of graph clustering?

Answer 72

It is very good at capturing non-blob-like clusters, or clusters with atypical shapes. This can be very useful

Question 73

ML: At an extremely high level, how does graph clustering work?

Answer 73

Form a graph from your training points, connecting points that are similar.

Then, make graph cuts which separate dissimilar points to form your clusters.

Question 74

ML: What method is used to do graph clustering with more than 2 clusters?

Answer 74

Spectral embedding (it uses some fancy linear algebra that is related to graph-based dimensionality reduction, but not going to get into weeds here.)

Question 75

402: What is the “optimal” regression function µ(x), and why is it optimal?

Answer 75

The optimal regression function µ(x) = E[Y|X=x]; it is the expected value of the true function y=f(x) at every point x.

This is the “optimal” regression function because it minimizes the expected mean squared error:

E[(Y-µ(x))²]

Question 76

402: What is the difference between parametric and non-parametric bootstrapping?

Answer 76

In parametric bootstrapping, we sample new simulated data from a model (which is parameterized, hence the name), and that model is learned from the actual data we have.

In non-parametric boostrapping, we don’t learn a model, and instead just resample the points we already have.

Question 77

402: What are the 3 main types of bootstrapping learned in 402?

Answer 77

Model-based bootstrapping, residuals resampling (which still involves a model, but uses it differently), and case resampling

Question 78

402: What purpose does bootstrapping serve, and how does it do so?

Answer 78

Bootstrapping allows us to get an approximate sampling distribution for a statistic of our data.

So typically we have a dataset of n values X_i, and from it we will calculate a variety of statistics: mean, standard deviation, regression coefficient for a model you’re fitting to the data, difference in MSE between 2 models you’re fitting, etc. But for each statistic, you get one value of the statistic per dataset, and to get an (approximate) sampling distribution for a statistic, you need to simulate many datasets, then use them to find the sampling distribution of the test statistic, which you calculate for every simulated dataset.

Question 79

402: What is the Bootstrap Principle? In other words, what is the 3-step high-level/theoretical process for bootstrapping?

Answer 79

Question 80

402: Why is it so often useful to use bootstrapping to get an approximate sampling distribution of a statistic?

Answer 80

We use statistics to make estimations about the underlying data: maybe want the mean, or a coefficient in a model, or the difference in MSE between 2 models. By finding an approximate sampling distribution of such a statistic, we can approximately quantify the uncertainty around our estimated value. So if we have a sample mean estimating the expected value of the data µ, we can use bootstrapping to find a confidence interval, or a standard error, or a variance, etc. And quantifying our uncertainty regarding these estimates is always a responsible thing to do!

Question 81

402: How do we do bootstrapping with residuals resampling?

Answer 81

Residuals resampling: Here you have data in form of (x,y) pairs. You learn a model y~f*(x) (so this is actually parametric), and use it to get the n residuals from your original dataset. Then, for a resampled dataset, the x’s stay the same, but the y’s are f*(x) plus a resampled residual.

So to reiterate, each “simulated dataset” has the same x values, which are not simulated. What’s “simulated” is the y values: you find y from f(x), then add a resampled residual.

It really strikes me personally as a sort of hybrid between a parametric and non-parametric technique. You’re using a model, and generating a simulated value y from the model for each x. But then you get your residual, which is resampled in a quasi-non-parametric sort of way.

Question 82

402: How do we do bootstrapping with case resampling?

Answer 82

This one’s pretty simple: each simulated dataset is n full, unaltered data points resampled from the original data, with replacement.

Question 83

402: How do we do bootstrapping with model-based simulation?

Answer 83

We learn the parameters of some model from the data; then, we use the model to sample entire datapoints.

Example 1: Say we have 1-dimensional datapoints X_i. We might learn a normal distribution, then sample points from that distribution.

Example 2: Say we have datapoints of (x,y) pairs. Here we would need to generate a full (x,y) pair from a learned model. Perhaps, for example, we learn a normal distribution for x, and then a regression model for y given x. (We didn’t go into this much in class, and tended to use residuals or case resampling instead.)

Question 84

402: How do we choose between our 3 bootstrapping options for, say, data in the form of (x,y) pairs? What factors are considered?

Answer 84

Our 3 options have varying levels of assumptions: model-based bootstrapping requires more assumptions about the underlying data than residuals resampling, and residuals resampling requires more assumptions than case resampling. (Case resampling basically assumes nothing; residuals resampling learns a model and assumes that the distribution of residuals is the same for any (x,y) pair; and model-based bootstrap assumes that it can make full (x,y) pairs from a model that the data actually fits).

More assumptions means more efficient use of the data if you are correct: you are fitting a more specific model if you use more assumptions. This means that your confidence intervals will be tighter, which is good.

So basically, you want to choose the model with the most assumptions that you can still feel confident about. We can rarely feel confident about model-based simulation, so we rarely pick it. If the residuals assumption appears true, we pick residuals resampling; otherwise, we just use case resampling and settle for wide confidence intervals.

(See 6.8 in the text, a brief section, for a complete discussion if desired)

Question 85

402: At a high-level, how do we use kernels for density estimation of a pdf f(x)?

Answer 85

We “smooth out” each datapoint by putting a “kernel” at each datapoint to act as a “little pdf” for that point. The kernels will generally look like normal distributions; if f(x) is higher than 1-dimensional, then a multivariate normal. We then just sum all of the little pdfs together into an estimated real pdf (the sum is normalized so it’s a real probability dist).

The following picture is for a janky example where the width of the normal distributions was too small and where the data weren’t to enough decimal places, but it illustrates the idea:

Question 86

402: What mathematical objects do we use for causal analysis?

Answer 86

DAGs (directed acyclic graphs)

Question 87

402: In causal inference DAGs, what does a vertex represent, and what does a directed edge mean?

Answer 87

Each vertex is one of the features of your data being measured. For example, if X = [x₁, x₂,…], then a vertex would be x₁ or x₂.

An edge between 2 attributes means that the two attributes have a nonzero covariance, or a nonzero linear correlation. The direction defines the causal influence, so A -> B means A influences B.

Question 88

402: In causal inference, why must our graphs be acyclic?

Answer 88

Because we assume that there are no causal cycles.

(for some reason; it seems logical at times. The reasoning was something about how it’s time based, and with A -> B, a change in A results in a change in B later, and we can’t “go back in time” or something.)

Question 89

402: Given a correct DAG for causal inference, how can we make a regression that examines the causal impact of A on B?

Answer 89

We must control for a set of variables that satisfies the backdoor criterion.

In programming terms, this means we include all of the variables in the set, along with A, as predictors of B, and then look at the coefficient of A in predicting B.

Question 90

402: When predicting B from A using a causal graph, what properties must a set of factors S have to satisfy the backdoor criterion?

Answer 90

S must:

1. Block all backdoor paths from A to B (so any paths with an edge pointing out of A and into B, except for the “direct” path)
2. Contains no descendants of A

Question 91

402: What is a fork, a chain, and a collider?

Answer 91

Fork: A <- B -> C

Chain: A -> B -> C

Collider: A -> B <-C

Question 92

402: When is a Fork (A <- B -> C), Chain (A -> B -> C), or Collider (A -> B <-C) open?

Answer 92

Forks and chains are open when B is not controlled for. Colliders are open when B is controlled for.

Question 93

402: When is a path from A to B open?

Answer 93

When it is open at every vertex in between, meaning that every vertex in the middle of a fork or chain is not controlled for, and every verted in the middle of a collider is controlled for.

Question 94

402: What are the 2 main ways to get a causal DAG?

Answer 94

1. Guess one (generally assisted by domain knowledge), and check if it’s correct.
2. Use a discovery algorithm.

Question 95

402: What is the best algorithm for finding a causal DAG learned in 402? What are its assumptions and limits?

Answer 95

The PC algorithm.

It of course assumes linearity, which can be wrong. It also sometimes can’t figure out the direction of an arrow, in which case you may have to account for both possibilities. Lastly, each relationship is found with some confidence, say 95%, and with a lot of relationships, some are likely to be wrong; so taking the DAG as gospel, or any causal inference DAG for that matter, can be risky.

Question 96

402: If you guess at a correct causal inference DAG (which assumes linear relationships between variables), how at a high level do we “check if a graph is correct”? Can we ever know?

Answer 96

We can’t really ever know for sure if a graph is correct. But, there are ways to check if it’s incorrect, and if you go through all of those and find no issues with your graph, you can start to feel confident.

You can check the assumptions: linearity for example.

You can also look at conditional independences among lots of different subsets of the variables, which can potentially disprove the presence/absence of an edge, or the direction of an edge. (Conditional independence can be considered somewhat intuitively, or using the fork/collider/chain rules. Can go back in course materials for more info.)

Question 97

ML: How do you specify a hyperplane classifier for D-dimensional x, and Y either 0 or 1?

Answer 97

Question 98

ML: What does it mean to “fold the intercept in” for a hyperplane classifier?

Answer 98

Rather than writing the hyperplane as w^Tx + b = 0, you write it as w^Tx = 0, and implicitly assume that the first (zeroth) entry in w is your intercept b, and the first (zeroth) entry in your x vector is a 1.

Question 99

ML: What is a simple way to draw a hyperplane classifier w^Tx = 0, as well as the direction of the arrow pointing towards y=1?

Answer 99

Just draw the hyperplane by normally drawing a line, by converting into y = mx + b form.

To figure out which side has which label and draw that arrow, do some easy-to-calculate sample point back in the original form of w^Tx = 0, and see whether w^Tx is above or below 0.

Question 100

ML: When would you use MAP estimation of a parameter instead of MLE estimation?

Answer 100

MAP allows you to include some prior distribution of the parameter before factoring in the data. So, if you have suspicions about the value of a parameter, perhaps because of domain knowledge, then MAP could be better as it will allow you to encorporate that knowledge.

Question 101

Answer 101

Question 102

ML: What is the goal of dimensionality reduction?

Answer 102

We want to take our D-dimensional dataset, and represent it using fewer dimensions (or fewer features). And we want to preserve as much of the structure and information in the data as we can: we want similar points in our original dataset to also be similar in the dimension-reduced dataset, and want dissimilar points to also remain dissimilar (by whatever measure of similarity makes sense in context).

Question 103

ML: What does PCA give you?

Answer 103

With D-dimensional data, PCA finds up to D new linear dimensions, or vectors, or “number lines” as I think of them, which are linear combinations of the original dimensions (e_1, e₂,…). Each of these dimensions is called a Principal Component, and the first is the vector v₁ maximizing the variance of Xv₁, the projections of the points in design matrix X onto the number line of v₁. The remaining principal components maximize the variance of the projection Xv_i while also making v_i orthogonal to all previous principal components. (All D principal components thus form a basis for R^D, as they’re all orthogonal.)

Using these principal components, you can choose k < D of them to represent your data in the k dimensional subspace preserving as much of the variance in the data as possible (I bet it’s actually an approximation of that, cuz it feels like it’s a greedy algorithm, but that’s the idea).

Question 104

ML: In PCA, what is a principal component? What is a PC score?

Answer 104

A principal component v_i is one of the new dimensions which you’re projecting your data onto, and using to store information.

A PC score Xv_i is the projection of all D-dimensional points in your design matrix X down on v_i. It is a nx1 vector, with each entry being a scalar showing the location of a point in X on the “number line” that is principal component v_i.

Question 105

ML: In PCA, what is proportion of variance explained?

Answer 105

For some subset of the D principal components, say k of them, the proportion of variance explained is how much of the variance from the original dataset is preserved by this k-dimensional representation. (Or what is explained by each individual principal component; both definitions work.)

Specifically, it is (I assume) the variance in the k-dimensional representation divided by the variance in the original data.

We are often interested in proportion of variance explained as a function of k, so we can see when we have a k high enough to explain a reasonable proportion of the variance, such as maybe 90%.

Question 106

ML: In PCA, what is a scree plot?

Answer 106

It plots proportion of variance explained vs number of principal components used, as a means of visualizing how much information will be preserved by each additional principal component.

This is the general idea, but there are many versions. Some plot number of PCs used vs eigenvalue associatied with its eigenvector, because these are related (as described in another flashcard). Another type, shown below, has the proportion of variance at each individual PC.

Question 107

ML: What is an intuitive explanation of proj_a(b), the projection of vector a onto vector b?

Answer 107

It’s just the component of a that’s in the direction of b. Think 2-d velocity calculations from physics: when we divide the velocity of an object into its x component and y component, that’s the velocity vector’s projection onto the vectors of the axes, (1,0) and (0,1), respectively.

Question 108

ML: What is an orthonormal matrix Q?

Answer 108

An orthonormal matrix is a square DxD matrix where every column has a length of 1, and all columns are orthogonal to each other. The columns thus form a basis for R^D.

Question 109

ML: What is a basis, with respect to a vector space?

Answer 109

A basis is a set of vectors such that any vector in the vector space can be represented as a linear combination of the vectors in the set.

Question 110

ML: What is the formula or equation satisfied by matrix M and its eigenvector v and associated eigenvalue ÿ (lambda)?

Answer 110

Mv = ÿv

(Mv = lambda*v)

Question 111

ML: When do we know that square matrix M has an eigendecomposition?

Answer 111

When it is real and symmetric.

Question 112

ML: Assuming square matrix M has an eigendecomposition, what is its eigendecomposition?

Answer 112

M = UDU^T, where D is a diagonal matrix with M’s eigenvalues on the diagonal, and U is an orthonormal matrix with the associated eigenvectores as columns.

(It is assumed as convention that the values in D are reordered such that |d₁₁| > |d₂₂| > …), and that the columns of U with the corresponding eigenvectors are reordered to match.

This is an extremely powerful decomposition with lots of truly great uses, such as direct applications to PCA, MDS, and spectral clustering.

Question 114

ML: What is the singular value decomposition, or SVD, of real matrix M with rank r?

Answer 114

Question 115

Answer 115

Question 116

Answer 116

Its entry at position i,j is the sample covariance of feature i and feature j (based on the observations/data points in design matrix X).

Question 117

ML: In PCA, once you have your top k principal components v_i, how do you get your k-dimensional representation of data matrix X?

Answer 117

X_new = XV_k, where the columns of V_k are the k principal components v_i.

In other words, you find all k PC scores, Xv_i, which is just the projection of each point x onto the number line of direction v_i, and then you combine all of those projections into your new representation X_new.

Question 118

ML: There are three common high-level ways to compute PCA. What are they? In other words, what 3 matrices can you do what three things to to get relevant information for PCA?

Answer 118

Given data matrix X, you can:

1. Find the eigendecomposition VDV^T of its covariance matrix (Sigma-hat)
2. Find the singular value decomposition of X = UD*V^T.
3. Take the inner product matrix XX^T and find XX^T = U(D*)²U^T, where U and D* the same as in option 2.

Question 119

ML: Say you do the calculations for PCA by finding the singular value decompositon of design matrix X = UD*V^T. How do you find the principal components (or the dimensions for the dimension-reduced representation), as well as the proportion of variance explained by each PC?

Answer 119

The columns of V are the principal components, and the corresponding values in diagonal matrix D* are the amount of variance explained. (So in order to get the proportion of variance explained for each PC, you’d take its entry in D* divided by the sum of all the entries in D*.)

Question 120

ML: Say you do the calculations for PCA by finding the eigendecompositon of the covariance matrix (Sigma-hat = VDV^T) of design matrix X. How do you find the principal components (or the dimensions for the dimension-reduced representation), as well as the proportion of variance explained by each PC?

Answer 120

If covariance matrix Sigma-hat = VDV^T, then the principal components are the columns of V, and the corresponding values in diagonal matrix D are the amount of variance explained. (Specifically, the absolute value of the entries of D.) (So in order to get the proportion of variance explained for each PC, you’d take the absolute value of its entry in D divided by the sum of all the absolute values of the entries in D.)

This means that for any dataset X, the PCs are just the eigenvectors of the sample covariance matrix, in order by the absolute value of their eigenvalues, and the eigenvalues define the proportion of variance explained.

Question 121

ML: Say you do the calculations for PCA by converting inner product matrix XX^T into XX^T​ = U(D*)²U^T. How do we find the PC scores?

Answer 121

UD gives the PC scores. We can thus do PCA dimension reduction using only the inner product matrix.

Question 122

ML: How do you Kernel PCA for some dataset, and what does Kernel PCA allow you to do?

Answer 122

Kernel PCA allows you to find nonlinear embeddings using PCA, which typically only finds optimal linear embeddings.

You’ll recall that you can do normal PCA by taking the inner product matrix as XX^T​ = U(D*)²U^T, where XX^T is the inner product matrix with (XX^T)_i,j = x_i^Tx_j.

Well instead, use the kernel trick and make a different similarity matrix, a kernel matrix K, where the entries K_i,j = k(x_i,x_j) for some nonlinear kernel. Then do the same decomposition into K = U(D*)²U^T for some other matrices U and D, and find the PC scores in the new nonlinear space as UD just as you would when using XX^T.

This way, you can find the PCA dimension reduction of X, but after transforming the points of X into any new subspace you want, likely a non-linear one, using kernels.

Question 123

ML: How does MDS work for dimensionality reduction, and what does it accomplish?

Answer 123

If you have n points, and you have a matrix of distances between points, then you can find a similarity matrix M, similar to XX^T, on which you can perform PCA to get a dimension-reduced version of the data. (Each entry M_i,j is the distance between points i and j.) But, you can use any distance measure, including non-euclidean distance measures, which will help you find nonlinear dimension reductions which can preserve nonlinear structure in the data.

Question 124

ML: How does ISOMAP work for dimensionality reduction, and what does it accomplish?

Answer 124

You’ll recall that you can use PCA to find a linear dimension reduction of data using only similarity matrix XX^T. Additionally, in MDS, you feed PCA a similarity matrix that instead uses some non-euclidean distance measure.

Well, ISOMAP is simply an instance of MDS where the distance matrix is calculated using graphs. You make a graph where the vertices are your data points, and every edge from point i to j has a weight of their euclidian distance apart. Then the graph distance is the shortest path in the weighted graph from i to j; feed these non-euclidean distances into MDS, and you’ll get a nonlinear embedding which preserves structures like swirls or curves.

Question 125

ML: What is overfitting?

Answer 125

Overfitting is when you allow your model to learn the patterns in the training data too well, so that it follows the noise in the training data. This results in validation error that is much higher than training error. This typically happens when your model has too much complexity (so that it can learn all the idiosyncracies of the training data), and/or when you don’t regularize.

Question 126

ML: What does the graph of train error and test error vs model complexity look like?

Answer 126

Question 127

ML: In general, what is Regularization? And what is its purpose?

Answer 127

Regularization is when you limit the values your models parameters can take, or (more commonly) penalize your model for taking certain values.

Typically, this looks like penalizing your model for having parameter values/coefficients that are large nonzero. So your objective function now needs to balance model fit and model complexity.

Regularization is generally used to combat overfitting.

Question 128

ML: What does Regularization do to bias and variance? And what causes these changes?

Answer 128

Regularization increases bias: by penalizing a model for taking certain forms or parameter values, it becomes less capable of taking the form of the true model in certain situations; its ability to fit the data decreases.

Conversely, variance decreases, meaning that the model becomes less impacted by noise and fluctuations in the data. This is really the whole point of regularization: to combat overfitting to noise.

Question 129

ML: Generally speaking, when should you regularize your model?

Answer 129

Almost always. This is a good thing to remember; it was driven home in 462, but often falls by the wayside.

Question 130

ML: What is the general form of an objective function for finding your parameters beta (B₁, B₂,…) using ridge regression?

Answer 130

If you have p parameters, it takes the value below for some balancing value lambda. (Note you don’t regularize the intercept B₀)

Question 131

ML: What is the general form of an objective function for finding your parameters beta (B1, B2,…) using lasso regression?

Answer 131

If you have p parameters, it takes the value below for some balancing value lambda. (Note you don’t regularize the intercept B₀)

Question 132

ML: When doing regularization, why does shrinking the coefficients combat overfitting?

Answer 132

A coefficient basically says that there is a substantive relationship between one variable and your output variable. By shrinking the coefficients, or penalizing large coefficients, you limit the number and magnitude of substantive predictive relationships that your model says exist.

This in theory means, if tuned right, it can only capture the important or “real” trends, but can’t capture the minutia in the noise of the training data. Hence, it combats overfitting.

Question 133

ML: What are the pros and cons of lasso regression vs ridge regression?

Answer 133

Lasso regression particularly wants coefficients to be zero (rather than them being very small, but not zero). This means it will result in more zero coefficients, so it makes models that are more interpretable and that show which variables “actually matter”.

However, lasso thus zero’s out small relationships, which means it has more bias. Ridge doesn’t do this: the difference between 0 and .001 isn’t as big for ridge, which results in basically no zero coefficients. Thus, ridge would make more sense if you’re more concerned with accuracy than with interpretability.

Question 134

ML: When using regularization, what will the regularized parameters look like as lambda goes to 0? To infinity?

Answer 134

As lambda goes to zero, we move towards no regularization, so the solution moves towards being the same as if we hadn’t regularized.

As lambda goes to infinity, our model will just make all coefficients go to zero, as this minimizes the objective function.

Question 135

When regularizing, what does a high lambda mean? A low lambda?

Answer 135

A high lambda means that the shrinking of coefficients has a lot of weight in the objective function, and so combatting overfitting will be very important to this model.

Conversely, low lambda means more liberty to have high coefficients, and we are more able to fit training data.

Question 136

ML: Generally, when regularizing a model, what will plots of training and test error vs lambda look like if, say, no regularization would lead to an overfit model?

Answer 136

Increased lambda means more regularization.

As such, training error will monotonically increase as lambda increases.

Test error will decrease, then increase. So there will be an optimal lambda value where test error is minimized.

Question 137

ML: Which of the following plots of parameter values vs lambda is for ridge regularization, and which is for lasso regularization? How can you tell?

Answer 137

The one where things go quickly to zero, or the right one, is lasso, because lasso zero’s out coefficients.

The one where coefficients asymptote towards zero is ridge, as it decreases coefficients but doesn’t actually zero them out.

Question 138

ML: Why is the equitable scaling of your different variables important when regularizing?

Answer 138

If the scales of your variables are very different, then a small parameter might mean a large change, or a large parameter might be a smart change. Because regularization tries to decrease parameter values without considering which variables they correspond to or what those variables’ scales are, the incentives for decreasing the influence of certain variables will be accidentally too high or too low based on scale.

Question 139

ML: When regularizing, why do we not regularize the bias term b?

Answer 139

The goal of regularization is to shrink coefficients of predictor variables, making it less likely our model will say it has predictive value.

Take Y = aX + b for example. By shrinking our learned value for a, we limit the amount of influence our model can percieve that X has on Y.

But b doesn’t describe how much impact X has on Y. It merely offsets the relationship and says what Y is likely to be when X is zero, but it doesn’t impact the model’s perception of whether X is related to Y.

So if we were to regularize b, and penalize our model for having large values of b, we would be limiting our model’s ability to find the correct relationship (increasing bias) without helping its ability to combat overfitting, or finding substantive relationships between variables which don’t actually exist. Hence, don’t regularize b.

Question 140

ML: What is a basic example of a regression algorithm and a classification algorithm where ridge or lasso regression are often used?

Answer 140

Linear regression and logistic regression (because they fit the formulas and ideas we’ve learned so well).

Question 141

ML: In classification, what might happen if your training set is imbalanced, and one label is very common or very uncommon?

Answer 141

Our classifier becomes biased towards predicting the label that is more common in our training set, hurting its predictive ability.

Question 142

ML: In classification, what are 3 ways to combat an imbalanced training set, where one label is way more common than the others?

Answer 142

Downsampling: Only train using a subset of the points with the common label

Upsampling: Duplicate the training points with the less common label and use them multiple times in the dataset.

Weights: Changes weights of your problem in a variety of ways. For example, penalize the model more for errors when the correct answer was the uncommon label.

Question 143

ML: With a bias vs variance perspective in mind, what are two common high-level ways to improve your model?

Answer 143

Change the amount of regularization (more regularization is bias up, variance down)

Or change the model complexity (more complexity means bias down, variance up)

Question 144

ML: If your training error is much lower than your test error, does this mean your model’s variance is too high, or its bias is too high?

Answer 144

Variance

Question 145

ML: What are a few high-level model traits that are good to keep in mind when choosing a model?

Answer 145

• Model flexibility, or ability to fit a variety of true underlying models
• Ability to capture nonlinearity
• Interpretability
• Ability to handle irrelevant features well

(Don’t necessarily need to get all of these or get it exactly right, but these are good things to keep in mind)

Question 146

ML: What is a common advantage that both lasso-regularized models and random forests have in common? And why is this useful?

Answer 146

They both handle irrelevant features very well, which means you can throw a lot of features at them in hopes of finding a couple good ones, even if you suspect lots of them have little or no predictive power.

Question 147

ML: When training a model using a simple train/validation/test split (not cross validation), what are the general high-level steps?

Answer 147

1. Split off some of your data, say 10 or 20%, to act as test data. Do this first.
2. Split off more data to act as your validation data; leave the rest as training data.
3. Try a bunch of models by training them with the training data, then finding their approximate out-of-sample error by predicting on the validation data.
4. Choose a final model.
5. Approximate your final model’s true out-of-sample error by training it on both the training and validation data and finding its error on the test set.
6. Train the model on all of your data, and deploy it to do whatever it needs to do in the real world.

Question 148

ML: How do you train a model using cross-validation? How does it differ from normal validation?

Answer 148

With normal validation, once you’ve set aside your test data, you split your remaining data into train and validation data. You train all your models on the train data, then validate them with the validation data. You pick a model and test it on the test data.

With cross-validation (say with k folds, such as 5 or 10), after you set aside test data, you instead divide it into k groups, or k “folds”. For every model you try, you train it on k-1 of the folds and find its validation error on the remaining fold, and you do this for each of the k folds. Finally, you get your validation error by averaging all k of your error measures on each of the folds. (So you train your model k times rather than once when you are validating.)

Question 149

ML: What are the pros and cons of cross-validation vs normal validation? Which of these makes cross-validation more common and popular than normal validation?

Answer 149

Cross-validation wastes less training data during the train/validation part of the model fitting process. It also decreases the variance that appears when you split train and test: what if an outlier shows up in the validation set, or what if it doesn’t? For these reasons, cross-validation is much more common in practice than normal validation.

However, cross-validation can take a long time: the more folds you have, the longer it’s going to take to do all that training, whereas with normal validation you only train once.

Question 150

ML: When cross-validating, is more or less folds better? What is the “ideal” number of folds? What is the intuition behind this?

Answer 150

Generally more folds is better, and you want as many folds as possible. The “ideal” cross validation is leave-one-out cross validation or LOOCV, where each datapoint is its own fold, with the intuition being that the more data you use to train for each fold, the better you simulate how the model will perform on actual held-out data.

But of course, more folds means more time, and thus LOOCV is often not realistic. 5-fold and 10-fold CV are common and tend to do the trick.

Question 151

ML: In the train-validate-test split, why do we need a test set to get an accurate idea of our model’s out-of-sample error? Why can’t we use the model’s validation error for this? (Equivalently, why do we need a test set when doing cross-validation rather than just using cross-validation error?)

Answer 151

Any choice that you make in model selection when working with training and validation data has the risk of overfitting to the training and validation data. The characteristics of your training and validation data that cause you to make certain decisions might be noise.

Additionally, if you try enough models, one of them is likely to get a low validation error simply due to random chance.

For these reasons, you need data to test your model on after you choose your model to accurately estimate your out-of-sample error. You need the data that you use to assess out-of-sample error to not be involved in selecting a model in any way, otherwise it is possible that you are underestimating your error for these reasons.

Question 152

ML: When choosing a model for a given task, what choices need to be made or actions need to be done after you set aside your test set, rather than before? And why?

Answer 152

All decisions and all actions. Or as many as possible.

You shouldn’t do feature engineering, or consider candidate algorithms, or decide how to define an outlier, or even curiously look at a histogram of your data before you set aside your test data.

This is because all of these decisions are a part of your model selection process, and you need a test set which wasn’t used for model selection in order to get an accurate, unbiased estimate of your final model’s out-of-sample error.

Question 153

ML: One concern about not looking at your test data before splitting it off is that it might contain weird or unexpected data points that cause your final model to crash or fail, such as a new category in a categorical variable. What is a response to this concern?

Answer 153

If you have enough data (or as your sample size n tends to infinity), your odds of seeing unexpected new things and/or things that cause bugs should be low, as your training and validation data should be representitive of all available data.

Question 154

ML: Discuss the potential importance of feature engineering when finding an effective model.

Answer 154

It’s very important: finding the right features to feed into your model can easily be as important or more important as what algorithm you choose to use, and deciding/brainstorming these features will often take up a large majority of your time when trying and selecting models.

Question 155

ML: With the train/val/test split and the importance of a held-out test set in mind, what is a good way to think about the definition of a “model”? And why?

Answer 155

A model can really be thought of as any aspect of the algorithm that outputs your predictions. This of course includes the algorithm you choose (random forests, linear regression, etc) and the values of the model’s parameters, but it also includes the features that your model takes as inputs, or how your model defines and handles outliers. That features idea is very important: the presence or absence of features is a part of your model; feature engineering is a subset of model selection.

This is a good way to think because it emphasizes the importance of not making any decisions or looking at anything before you set aside your test set. It also encourages you to think deeply about (and remember to cross-validate) aspects of model selection like feature engineering that you might think less important than, say, choosing your algorithm.

Question 156

ML: During model selection, what sorts of decisions should you cross-validate? How do you cross-validate these decisions? And why do you choose to cross-validate them? What practical concerns arise and how do you address them?

Answer 156

You want to cross-validate as many decisions as possible. This includes the normal stuff like the value of your hyperparameters, but also which algorithm you use, which features you choose to include, etc.

To cross-validate these things, you just find a cross-validation error for each combination of those decisions. So you try your algorithms with and without each feature you’re considering, for each of your candidate algorithms, and each of their possible hyperparameter values.

The issue with this strategy is it takes a lot of time, as you have a lot of combos. You address it by taking shortcuts that seem reasonable to you, and that your intuition says would still lead to a good final model. Maybe you don’t try every combination of features, or every value of a hyperparameter. Maybe you choose an algorithm with only a couple possible sets of features and a couple sets of hyperparameters, then hone in on that algorithm and try more combos of features, more candidate features in general, and spend more time on more possible hyperparameter values.

Question 157

ML: At an introductory level, what is training data used for and what is validation data used for when training a model? What is an example of each of these?

Answer 157

• Training data* is used to learn the values of your model’s parameters. For example, when learning a neural network, your training data would teach the model its weights and bias terms
• Validation data* is used to learn the values of the hyperparameters. For example, in KNN, you might use validation data to decide k, the number of neighbors, which is a hyperparameter. In the neural network example, you might use validation data for defining number of layers, nodes per layer, which activation function, etc.

Question 158

ML: What do we use methods like gradient descent for?

Answer 158

We use gradient descent to minimize (or maximize) differentiable objective functions, or to find the value of x sucht that f(x) is minimized.

f(x) needs to be differentiable because we need to take its derivative in order to get the gradient.

Question 159

ML: Why would we use an iterative method like gradient descent to minimize a function f(x) rather than just solving for its true minimum with calculus?

Answer 159

Solving it with calculus is often extremely time-consuming or impossibly time-consuming, especially when you need to minimize an objective function with respect to, say, 1000 parameters as with NNs.

Question 160

ML: What is a common problem you will run into when using an iterative descent method like gradient descent to minimize a function f(x)?

For what type of functions are you guarenteed not to have this issue?

If you don’t have this type of function, what is one way to combat this issue?

Answer 160

Depending on where your starting point is, you may descent to a local minimum rather than a global minimum, but your algorithm will still stop: it can’t take a small step in a direction and improve its situation.

This won’t happen with convex functions, or where the gradient is always “negative” or zero (this is how to think of convexity in say 2 or 3 dimensions; the terminology might differ at higher dimensions)

To combat this issue for non-convex functions, you can try several randomly chosen starts and see which returns the minimum; it still doesn’t guarentee a global min though.

Question 161

Answer 161

The gradient of the function with respect to theta is just a vector of the partial derivatives of the function with respect to each of the p parameters in theta.

Intuitively (especially when visualizing say 3 dimensions), it is the direction of the n-dimensional slope, or the direction in which a small step would most productively move you towards optimizing the objective function. (Technically, you might move in the opposite direction, but same idea.)

Question 162

Answer 162

Question 163

Answer 163

Question 164

ML: In stochastic gradient descent, why do we feel comfortable taking small steps in the direction of the gradient for only one of the training points, when what we’re really trying to optimize the gradient with respect to the entire training set?

Answer 164

If you choose the point randomly, the expected value of the gradient with respect to a single point equals the gradient with respect to all n points.

Question 165

ML: What is an epoch?

Answer 165

A single pass throught the entire training set.

Question 166

ML: Why is SGD often faster and more effective than normal gradient descent?

Answer 166

Finding the gradient with respect to the entire dataset takes a long time. (Specifically, I believe it takes about equal time to find the gradient with respect to each of the individual points, as I believe it’s basically just a sum of those). So getting one update, which is albeit definitely in the direction of the gradient, takes a long time.

Conversely, SGD may make some updates in the “wrong” direction, but you get to make n updates in the time normal gradient descent needs to make only one. In practice, this typically leads to faster convergence to the same result.

Question 167

ML: What is mini-batch gradient descent, and why is it sometimes better than both normal GD and SGD?

Answer 167

In normal GD, you make updates with respect to the entire datapoint; so, your update is always in the right direction, but updates take a long time.

In SGD, you make updates with respect to a single datapoint; so, your update may be in the wrong direction, but the expected value of the direction is correct, and you can make many updates quickly.

In mini-batch gradient descent, you combine these ideas by updating with respect to small subsets of the training data each time. This can sometimes lead to a happy medium between making updates quickly, and often being in an approximately correct direction.

Question 168

ML: If we have a hyperplane classifier in the context of linearly separable data, what is the margin of the hyperplane classifier?

Answer 168

The distance from the hyperplane to the closest point

Question 169

ML: How does hard-margin SVM work? What does it try to maximize, and under what constraints?

Answer 169

Question 170

ML: Why does hard-margin SVM typically not work? How does soft-margin SVM fix this?

Answer 170

If the data aren’t linearly separable, no hard-margin solution exists, because the data can’t be perfectly classified with a hyperplane classifier.

Soft-margin SVM fixes this by allowing some points to cross the hyperplane without having the solution violate the constraints.

Question 171

ML: What is a support vector in SVM? What does it mean in hard-margin and in soft-margin SVM?

Answer 171

A support vector is a point that has an influence on the final solution.

For hard-margin, it is one of the points on the margin of the hyperplane.

For soft-margin, it is one of the points that is on the margin or within it, including points that are misclassified.

Question 172

ML: What is the optimization being done in soft-margin SVM?

Answer 172

Question 173

ML: Intuitively, how are we solving the classification problem when using soft-margin SVM?

Answer 173

Question 174

Answer 174

Question 175

ML: In soft-margin SVM, how does increasing the value of tuning parameter C

• The value of the margin M
• The number of points that influence the boundary
• The variance of the classifier
• The bias of the classifier

Answer 175

A higher C allows more points to have positive slack variables, and thus to be inside the boundary. The margin M is thus increased to accomodate the higher amount of points inside the margin.

Increasing C also thus increases the number of points that influence the boundary, as the boundary is only influenced by points on or inside the margin.

Because more points influence the boundary, variance goes down (we are less susceptible to outliers). Bias would I assume increase as a result, but I’m not sure why.

Question 176

ML: In soft-margin SVM, how is tuning parameter C related to misclassification error on the training data?

Answer 176

Because the sum of the slack variables is capped at C, and a slack variable above 1 means a point is misclassified, C is the maximum number of misclassified training points.

Question 177

ML: How does multi-class SVM work, i.e. where there’s more than two classes?

Answer 177

Similar to multiclass logistic regression, we just fit k binary-classification SVMs: one for each of the k labels, predicting whether it’s that specific label vs any of the others (we treat all other labels as a single label for each binary classifier). We then predict via:

Question 178

ML: What is the idea of the kernel trick? What two valuable advantages does the kernel trick give us?

Answer 178

Question 179

ML: How does using the kernel trick for SVM work? Where do we sub in the kernel?

Answer 179

Question 180

Answer 180

Question 181

ML: What is the l_p norm (as in l₀, l₁, etc) for integer values from 0 all the way to infinity?

Answer 181

Question 182

ML: What does a norm accomplish at a very high level?

Answer 182

It maps a vector to a non-negative scalar in a way that measures its “length”

Question 183

ML: What is the l₂ norm? What does it find, and how do we calculate it for a vector?

Answer 183

The l₂ norm, or the euclidean norm, is simply the distance formula: it’s the length of the vector in euclidean space.

If x = [1,5,2], ||x||₂ = sqrt(1² + 5² + 2²).

Question 184

ML: What is the l₁ norm? How do we calculate it?

Answer 184

For ||x||₁, you just sum the absolute values of the entries in x.

||x||₁ = |x₁| + |x_{<span>2</span>}| + |x₃|

Question 185

ML: In the context of machine learning, what is the key difference between the l₁ and l₂ norms, and in the outcomes they produce?

How does this concept impact the regularization techniques we’re familiar with?

Answer 185

Suppose we are trying to find a vector x that minimizes a norm, either the l₁ or l₂ norm. So in both cases, we’re trying to find a vector x whose entries are near zero.

The l₂ norm doesn’t care much whether an entry in x is exactly zero, or very nearly zero; as such, when we try to minimize the l₂ norm, we get a bunch of values that are very nearly zero.

Conversely, the l₁ norm does care a lot whether an entry in x is exactly zero, or very nearly zero; as such, when we try to minimize the l_{<span>1</span>} norm, we get a bunch of values that are exactly zero, whereas with the l₂ norm they weren’t quite zeroed out.

This pops up in regularization: when we do ridge regression, we’re minimizing the parameter vector over the l₂ norm, and so we get a bunch of values that are almost zero, but none that are really zeroed out. When we do lasso regression, we use the l₁ norm and thus get a bunch of parameters that are exactly 0.

There are tradeoffs here: lasso regression yields more interpretable results, but ridge regression is better at capturing very small relationships that lasso tends to just zero out.

Question 186

ML: What are the two different outputs we can use to evaluate a classifier

Answer 186

Most classifiers find the probability that a point has each possible label, and then predicts the label with the highest probability.

So, we can evaluate either the predicted labels, or the predicted probabilities.

(Note: The classifiers don’t exactly make probabilities, they make values between 0 and 1. But these values can often be interpreted as probabilities, especially if we choose to transform them into more of a probability distribution.)

Question 187

ML: Why might we want to evaluate the probabilities that a classifier outputs, rather than just the labels?

Answer 187

Oftentimes it’s important to know how likely the labels actually are, not just what the maximum-likelihood label: if a potential client has a 99% chance of signing a deal, we’ll prioritize them differently than if they have a 51% chance.

Question 188

ML: In the context of classifiers, what is calibration, or what does it mean for a classifier to be well-calibrated? How might we evaluate it for binary classifiers?

Answer 188

Recall that a classifier generally outputs the probability that a point has each label. A classifier is well-calibrated if the labels happen about as often as they’re predicted to happen.

So if, in every case where the classifier says a point has a 70% chance of being label A, about 70% of them are actually label A while the other 30% are something else, we have a well-calibrated classifier (at least for that predicted percentage for that label).

For binary classifiers, we can evaluate calibration using a bin plot. We group together all of the points where we predicted the odds of y=1 were between 0% and 10%, and then we see how many of those points were actually y=1. Similarly for 10% to 20%, and all the other bins.

Question 189

ML: What is the confusion matrix for a classifier?

Answer 189

For a classifier with k labels, it’s a k-by-k grid that plots the frequency of every predicted label vs every actual label, so we can see what types of errors the classifier tends to make.

For a binary classifier, it simply shows the number of true positives, false positives, true negatives and false negatives the classifier had, in the form of a 2x2 grid.

Question 190

ML: What is the sensitivity of a binary classifier?

Answer 190

It is the proportion of true positive’s, or of y=1’s, that we get right.

So it’s :

(true positives/[true positives + false negatives])

Question 191

ML: What is the specificity of a binary classifier?

Answer 191

It is the proportion of true negativess, or of y=0’s, that we get right.

So it’s :

(true negatives/[true negatives + false positives])

Question 192

ML: Why might a classifier really need to avoid false positives, but be alright with false negatives?

What about one that really needs to avoid false negatives, but be alright with false positives?

How does this relate to specificity and sensitivity?

Answer 192

Both of these cases occur when one error is much more costly than the other.

Say we’re trying to decide whether to administer a treatment that has few side effects. If we get a false negative, and incorrectly classify someone as “healthy”, then we don’t give them treatment, which is very costly. But, if we incorrectly say they’re “sick” and treat them when they don’t need it, it’s not as bad. Here we heavily prioritize avoiding false negatives, or we want sensitivity to be high.

Conversely, consider a spam filter. We’re okay with accidentally sending spam to the inbox (false negative), but don’t want to send important emails to spam (false positive). Now, we care a lot about the specificity of our classifier being high, as we want to avoid false positives.

Question 193

ML: How to we alter a binary classifier we’ve already trained to make a tradeoff between specificity and sensitivity?

At a high level, how would we instead accomplish this prioritization/tradeoff during training rather than after?

Answer 193

Classifiers output a probability that y=1 on a given point. Typically we label a point with a 1 if the probability is above 50%, but we can change the threshold that the probability must reach to label a point as y=1.

If we only label it y=1 if the probability of y=1 is above 75%, then we are okay with false negatives, but really don’t want false positives; we’re prioritizing specificity.

Conversely, if we label it y=1 whenever the probability of y=1 is above 25%, then we are okay with false positives, but really don’t want false negatives; we’re prioritizing sensitivity.

Another option would be to initially train the classifier so a false-negative causes higher loss in the loss function than a false positive, or vice versa. So we would have different loss amounts L₀ and L₁ for the two different errors.

Question 194

ML: When false-negatives are much worse than false-positives, do we want a classifier with high sensitivity, or high specificity? What about when false-positives are much worse?

Answer 194

Sensitivity describes the probability that we label a point y=1 when it is in fact y=1; it’s the probability of avoiding a false-negative.

Specificity describes the probability that we label a point y=0 when it is in fact y=0; it’s the probability of avoiding a false-positive.

So, we want high sensitivity when false-negatives are bad, and high specificity when false-positives are bad.

Question 195

ML: For a binary classifier, what is an ROC curve? What is the AUC, and do we want our classifiers to have a high or low AUC?

Also, what is the ROC curve of a “random” classifier, and what is its AUC? (You’ll have to define what “random” means in this context.)

Answer 195

Recall that our trained binary classifier outputs a probability p that a point x has label y=1, and we can tradeoff the sensitivity and specificity of our classifier by moving the threshold of this probability where we predict y=1. So for some value t, we predict y=1 if p > t. It is high, we are avoiding false positives and thus have high specificity; if t is low, we are avoiding false negatives and thus have high sensitivity.

A curve on an ROC plot shows a classifier’s sensitivity and its specificity at every possible value of threshold t, which can be anywhere in [0,1]. It plots (1 - specificity) on the x axis, and sensitivity on the y axis.

What we want is classifiers whose curves are bowed out to the left, because then for each value of t they do a good job with both sensitivity and specificity. In this case, the classificer has a high AUC, or area-under-the-curve. We want high AUC, as it basically means our classifier is accurate.

The diagonal curve on the ROC corresponds to a random classifier, where our probability value p is randomly chosen from the interval [0,1], and then we threshold that probability for some threshold value t. The AUC of this curve is 0.5.

So a curve on the ROC plot is a classifier, and point on the ROC plot is a classifier-threshold pair. The top-left corner is a classifier-threshold pair always predicts the label correctly, and the bottom-right always predicts incorrectly. The bottom-left always predicts 0, and the top-right always predicts 1.

Question 196

ML: What does linear regression try to find for a dataset of (x,y) pairs?

Answer 196

Question 197

ML: Why is linear regression so popular?

Answer 197

It’s very common

It’s very easy to understand

The math is simple and well-known (I’m not going to memorize it, but it follows from the statement of what it’s trying to minimize.)

Question 198

ML: What 4 assumptions can be made when doing linear regression?

Answer 198

Question 199

ML: Which of the 4 linear regression assumptions need to be true in order to get the optimal linear predictor for the data.

Answer 199

None. The least squares formula will always form the optimal linear predictor for that dataset.

However, if the assuptions are wrong, that linear predictor won’t match the actual underlying model that produced the data. In other words, without the assumptions, the linear regression won’t be “correct,” or useful in modeling these data or other data from the same source.

Question 200

ML: Which of the 4 linear regression assumptions need to hold in order for the optimal linear predictor you get to be an accurate representation of the underlying model that produced the data?

Answer 200

i.i.d. data, linearity, and heteroscedasticity.

(pretty sure on heteroscedasticity, could check that)

Not gaussianity. That’s not needed.

Question 201

ML: When do we need the gaussianity assumption for linear regression?

Answer 201

Whenever we’re making confidence intervals or prediction intervals, be them for our coefficients, point predictions, etc.

Question 202

ML: In linear regression, what is the difference between a confidence interval and a prediction interval?

Answer 202

In the context of a point prediction, so predicting Y from X, a confidence interval is a range for E[Y|X], and a prediction interval is a range for the actual value Y itself. Confidence intervals thus discuss the distribution from which Y came, whereas prediction intervals discuss the actual, currently-existant value of Y.

(I think. This is weird.)

Question 203

ML: How do we check the linearity assumption for linear regression?

Answer 203

Plot the residuals vs both the X values, or the predicted Y values. If there are any patterns in the residuals, linearity is not met. If the residuals look basically random, linearity may be correct.

You can also plot the squared residuals vs these values.

Question 204

ML: In regression, what are the residuals for your dataset X and model µ()?

Answer 204

A residual for a prediction Y*=µ(x) is Y - Y*, the difference between the real and predicted values.

Question 205

ML: In linear regression, how do we check heteroscedasticity?

Answer 205

Question 206

Answer 206

Question 207

ML: In linear regression, how do we check the i.i.d. assumption?

Answer 207

One option is to plot your points vs some axis like Time, and assure that there is no pattern among points close in time. Basically look at ways the points might be related to one another, and see that they’re not, and that there is no pattern.

(This one was less well-defined in class)

Question 208

ML: In linear regression, how do we check the gaussianity assumption?

Answer 208

Make a Q.Q. plot (or quartile-quartile plot) of the residuals.

You’re seeing where the quantiles (or the “lines” demarking percentiles) are in the observed distribution of residuals, vs what these quantiles would be if the residuals followed a normal distribution. If it forms a line with a slope of 1, the normality assumption is probably correct; if not, then probably not.

Question 209

402: What did we learn that we should almost always use in place of linear regression?

Answer 209

An additive model

Question 210

402: What is a linear smoother, and how is it used for regression on a dataset of (x,y) pairs?

Answer 210

When given a new X, we predict the Y by taking a weighted sum of all the Y’s in the training set. The weighting w(x_i,x) is meant to be high when the points are “similar”, and low otherwise.

Question 211

402: What is knn regression?

Answer 211

In knn regression, we predict Y for a new X by just averaging the Y’s of the k X’s in the training set that are nearest to our new X. It is one option for nonlinear regression.

Recall that a linear smoother predicts Y for a new point X by taking a weighted sum of all the Y_i’s from the training set, for some weight function w(x_i,X) meant to express similarity between the two x’s.

KNN regression is just this, where the weight is 1/k if x_i is one of the k nearest neighbors of X, and 0 otherwise.

Question 212

ML: When we think about linear regression as a linear smoother (or as a regression that outputs a weighted sum of the training Y’s as the predicted Y), what strange phenomenon do we see?

Answer 212

The (x,y) pairs farther from the mean have a larger weight on the prediction than closer ones.

So basically, the farther out a point is, or the more outlier-ish it is, the more impact it has on predictions.

Upon inspection, this makes sense if the underlying model is actually linear, but is very weird otherwise.

Question 213

402: At a high level, how does kernel regression work? What are the key things we need to know about kernel regression?

Answer 213

We have a dataset of (x,y) pairs, and we predict Y for a new X by taking a sum of the y’s from the dataset, weighted by how close each y’s x value is to the X being analyzed.

Kernel regression weights points closer to X more heavily, and points farther from x less heavily.

The weight is found using a kernel k shown below. Often k is a gaussian.

• The bandwidth h determines how quickly the weight changes as we move away from our X value.*
• We tune h as a hyperparameter via cross-validation to get the best predictions.*

Question 214

402: In kernel regression, what happens when bandwidth h is too high and approaches infinity, or when h is too low and approaches 0? How does this relate to the bias-variance tradeoff?

Answer 214

The banwidth h is in the denominator of the term that determines how differently we weight close points and far points.

When bandwidth is high, the differences in weights will be small, so we will encorporate all points more equally into the prediction. As h approaches infinity, we will thus get to a prediction of just the mean Y value in the dataset. So, as h rises, variance decreases, but bias increases.

Conversely, when bandwidth is low, nearby points have higher relative weight and matter more. As h approaches 0, it turns into 1-nearest-neighbor regression, where we just predict the label of the nearest neighbor.

Question 215

402: What does it mean for a model to be universally consistent?

Answer 215

As n goes to infinity, the learned model must converge to the actual underlying model.

Question 216

402: Is kernel regression universally consistent? What about knn-regression, additive models, and linear regression? And why does this make intuitive sense?

Answer 216

Kernel and knn regression are universally consistent. Linear regression and additive models are not.

This means that given enough data, kernel and knn regression are guarenteed to converge to the true model, while the other two are not.

This is because linear regression and additive models both impose some kind of special structure on the underlying model: linear regression assumes it’s linear, additive assumes it’s additive. And if this special structure is wrong, it’ll never converge.

Kernel and knn regression just use the actual data, and they can take the form of any underlying model, so it makes sense that given tons of data, they will converge.

Question 217

402: If kernel regression is guarenteed to converge to the correct model, while an additive model isn’t, why would we ever choose to use an additive model over a kernel regression?

Answer 217

Additive models converges faster than kernel regression.

When we make assumptions about what type of underlying model we have, we can use data more efficiently, meaning we need less data to converge. (Of course, we will only converge if our assumptions about the model are correct, but if they are, we converge more quickly.) This is a general fact about all models, not just these regression models. An intuitive explanation as to why is, when we already know something about the model, we don’t need to learn it from the data, and we can use all of the data just learning the parameters within that model structure, rather than both figuring out the model structure and learning its parameters.

Kernel regression converges very slowly, in part because it makes no assumptions about the underlying model’s structure. Additive models assume that the model is additive; this significantly decreases the number of possible underlying models, and as such it converges significantly more quickly.

Question 218

402: Which of kernel regression, knn regression, additive models, and linear regression are parametric?

Answer 218

Additive and linear

Question 219

Why do we almost always prefer an additive model to a linear model?

Answer 219

Additive models are an easy step beyond linear models, with a lot of advantages.

A linear model is just a special case of additive models, and an additive model can fit a far wider array of underlying models without sacrificing that much efficiency or rate-of-convergence. So if the underlying model is nonlinear, additive might fit it while linear won’t. And if the underlying model is linear, an additive model can still fit it, and an additive model doesn’t need that much more data to converge to the true model than a linear regression does.

Question 220

402: What is the form of an additive model for predicting y from x? How does it compare to a linear model?

Answer 220

An additive model is similar to a linear model in that all the terms are being linearly summed (along with an intercept and a noise term) in order to get the prediction.

They differ because, in a linear model, a term is a variable with a coefficient. In an additive model, a term is that same variable x_i but fed into some partial response function, which can be nonlinear. This allows the modeling of nonlinear relationships, while still maintaining some of the speedup benefits of an additive structure.

Question 221

402: How does the computer, or the gam() function in R from the mgcv package, learn the additive model from the data at a high level? In other words, how does it choose from all the possible models to find the “best” one with the best splines?

Answer 221

It basically just maximizes likelihood, so it finds the model with the highest likelihood of producing that data. However, it does so while regularizing, or penalizing models that are too “wiggly,” in order to avoid overfitting data.

So we are finding the model that optimizes the objective function shown below, which balances maximizing likelihood and minimizing model complexity, using tuning parameter lambda. It also chooses a value for lambda, so it finds the optimal balance between data fit and regularization, presumably using something like cross-validation.

The model is a combination of smoothing splines , plus linear terms if desired or necessary. A smoothing spline, or partial response function, for a particular predictor is essentially the smoothed predicted outcome variable based on just that predictor.

A smoothing spline is calculated in gam by “summing a bunch of small functions in the data called basis functions.” I’m a little unclear on how this works, but basically gam() does not explicitly try a bunch of different functions like log(x_i), sin(x_i), x_i², etc, which is what we would expect based on the original definition of additive models. Rather, it uses fits a spline using a flexible, computational smoothing method that is capable of taking a form very similar to each of these possible underlying partial response function forms. It fits smoothers by iteratively improving each (improving them all, improving them all again…) until they all reach a local minimum and stop improving.

Question 222

402: What is the difference between an additive model and a generalized additive model?

Answer 222

Basically in generalized additive models, we get to specify the type of probability distribution from which our outcome variable is drawn. If we think our outcome has a normal distribution, or a poisson distribution, we can specify that, which (I assume) increases efficiency in using the data if it’s correct.

We can also specify if it’s categorical data and we want to do classification rather than regression, or if it’s geospatial data, or other more niche things, but I’m less familiar with these applications

Question 223

402: In additive models, how can we assess variable importance and/or perform variable selection?

Answer 223

If I recall correctly, we can assess variable importance by looking at the partial response functions. If there appears to be a relationship in the partial responses, the variable is probably important. If there doesn’t appear to be a relationship, or if “the confidence interval for the partial response contains zero for many values of the predictor variable” or something, then the variable probably isn’t that important. This is referring to variable importance in context, so a variable might have predictive power but be predicting things similar to other variables in the model, for example. But I’m remembering this somewhat hazily, would want to look back at notes and homeworks where we did this to get specific, if needed. Looking on piazza regarding HW12, this observing the partial response function seems to be used for seeing if the outcome and a predictor are independent or dependent, so yeah that assesses variable importance and predictive power in a sense. But this is described on piazza as an informal independence test; it is useful, but not completely rigorous.

We could also assess variable importance by seeing the drop in predictive ability caused by removing a variable! This was something we did often: fit the model with and without that variable, and see how much predictions got worse. We could use bootstrapping to get a confidence interval for the difference in MSEs of the two models and see if the confidence interval contains zero.

To actually perform variable selection, we can include select=TRUE in our gam() call, which penalizes the inclusion of variables in prediction, similar to lasso. We didn’t do this in class, but it exists and could definitely be useful.

Question 224

402: How do we handle interactions in GAMs in R?

Answer 224

The nature of additive models is to not include them by default, but if we suspect they’re there, we can add interaction terms to the model and smooth them using smoothing functions like te() and ti(), which take multiple variables while s() takes 1.

Question 225

402: In what sense are additive models a sort of balance between having an interpretable but non-robust model, and between having a robust model that is non-interpretable/a black box?

Answer 225

They aren’t as interpretable as say, linear models: they lack interpretable coefficients for each variable explaining the expected difference in the outcome variable as we vary the predictor. But we do have the partial response functions, which provide some interpretability of how different predictors impact outcome variables.

Additionally, they aren’t as robust as nonparametric models, as they require an additive form, but are still far more robust than linear models.

Question 226

402: What are some reasons Dr. Shalizi poses for R² and adjusted R² being useless in measuring both predictive error and goodness of fit?

Answer 226

Below is the formula for the “true” value of R² for a model: if we knew the true value of the coefficients of the optimal linear model, as well as the true values of the variance of X and noise epsilon, this would be the value of R². (Recall that even if the underlying model isn’t linear, there still exists an optimal linear model.)

Here, we can see that R can be arbitrarily close to 1 even if model fit is bad: just make Var[X] high or σ² low. Doing the opposite, we can make R arbitrarily close to 0 even if the model fit is perfect.

It also says nothing about your prediction error. R² is typically described as the proportion of variance in the output variable that our regression model explains. In other words, it’s the variance of our predictions divided by the variance of the actual values. Because it’s just a matter of comparing two variances, it doesn’t really say anything about prediction error. We could have a really bad model with similar variance in the outputs that has a “great” R².

Adjusted R² is very similar, it’s only difference is a constant to make σ²-hat an unbiased estimator of σ². It doesn’t solve any of these issues.

• (See section 3.2 here for more:)*
  http: //www.stat.cmu.edu/~cshalizi/mreg/15/lectures/10/lecture-10.pdf

Question 227

402/401: What is the correct way of interpreting a coefficient B_i in a linear regression? What is an incorrect way of interpreting it? Why is the latter correct while the former is incorrect?

Answer 227

Correct: B_i is the expected difference in the outcome variable Y between two points whose difference in X_i is 1, assuming the values of all other predictors are held equal.

Incorrect: B_i is the expected difference in Y caused by increasing X_i by 1.

The incorrect one is wrong because it assumes some sort of causal relationship. Our linear model by itself says nothing about what will happen if we change the value of X_i, it just says that on average, points with higher X_i have higher (or lower, depending on sign of Bi) values of Y based proportionally on B_i, which is what the correct interpretation is saying.

Question 228

402: If we’ve fit a (relatively) simple modelfor example, how can we use a more complex model to check whether the assumptions of our simple model is correct? (We can’t find definitively whether it’s correct, but we can find somewhat definitively evidence that it is incorrect.)

For example, suppose we think that our data are linear, and we find the optimal linear model from the data. How could we use an additive model to check whether our linearity assumptions are correct, and whether the underlying data are actually linear?

Answer 228

We are going to do a hypothesis test.

The null hypothesis is that the underlying data are linear. The alternative hypothesis is that they aren’t difference in MSEs between the linear model and the more complex additive model. If the null hypothesis is true, the difference in MSEs should be about zero, as the linear model can fit the data as well as the additive model; if the alternative hypothesis is true, the difference in MSEs will be nonzero, since the additive model will do a better job of fitting the data.

We start by finding the difference in MSEs on our actual dataset. To perform our hypothesis test, we need to find the p-value of our observation: we need to find the probability of seeing our observed difference in MSEs under the null hypothesis. If our observed difference in MSEs would occur with very low probability under the null hypothesis, we reject; otherwise, we fail o reject.

So, we need to simulate datasets under the null hypothesis that the data are linear. We will find the difference in MSEs on each of these datasets, to get an approximate distribution for the difference in MSEs. Each of our simulated datasets will have the same set of X values as the original dataset, and y values equal to the predicted y value under the linear model plus an error term. In the example in lecture 12, this error term is found by assuming gaussianity of the residuals, and sampling from a normal distribution with variance equal to the sample variance of the residuals. This is very similar to residuals resampling; I expect doing normal residuals resampling is also a viable option.

So, we get all these datasets, get our approximate distribution in the difference in MSEs between the two models under the null hypothesis, and look at the p-value of the difference in MSEs on the actual dataset to make a conclusion about the linearity assumption.

Question 229

402: What should be our go-to tool for model selection, or for comparing the difference in prediction error of two models, rather than R²?

Answer 229

Cross-validation, to approximate the MSEs of each model on out-of-sample data.

Question 230

402: What is a go-to way to measure variable importance in a regression model?

Answer 230

Fit the model with all the variables, as well as the model missing each of the variables. Find the difference in MSE when you remove each of the variables.

It would be good practice to use bootstrapping to find a confidence interval for the difference in MSE cause by removing each variable.