Topic 2 - Financial Planning Skills Flashcards
1
Q
What are the four important terms of considerations of investments?
Page 45
A
- Time value of money
- The effect of inflation and taxation
- Timing of cash flows
- Compounding frequency
2
Q
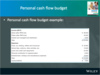
Personal financial statements can be prepared in two parts:
Page 46
A
3
Q
What do income and expenditure include?
When do you have net savings?
Pages 46-47
A
(002)
4
Q
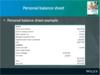
What does the personal balance sheet demonstrate?
What are assets, liabilities and net worth?
Page 48
A
5
Q
The personal financial statements can be used to calculate the following useful financial ratios to analyse the family’s financial position:
Page 49
A
6
Q
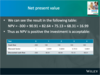
Calculate the net worth ratio:
Page 49
A
7
Q
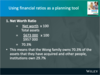
Calculate the liquidity ratio:
Pages 49-50
A
8
Q
Calculate the savings ratio:
Page 50
A
9
Q
Calculate the debt service ratio:
Page 51
A
- over 35% debt service ratio can indicate technical insolvency (not good!)
10
Q
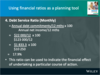
Why do people prefer cash now rather than later?
Page 53
A
11
Q
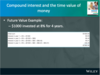
What is the compound interest of $1,000 invested for 4 years at 8% p.a.?
Study example on page 54
A
12
Q
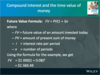
What is the future value (FV) formula?
Calculate the FV for $1,000 invested at 8% for 4 years.
Pages 54-55
A
13
Q
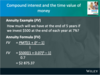
How much do we need to invest now at 8% to accumulate $1,360.49 in 4 years time?
Page 56
A
Note: The power of minus n is the reciprocal of the power of n, 1/n is the same thing as 1 exp -n or 1 to the power of minus n.
14
Q
How much will we have at the end of 5 years if we invest $500 at the end of each year at 7%?
Page 57
A
15
Q
What is the present value of an annuity of $500 for 5 years at 7%?
Page 57
A
16
Q
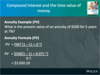
What’s the difference between the nominal and effective interest rate?
Pages 59-64
A
17
Q
Since the time value of money formula assumes annual compounding, to obtain the periodic interest rate (i), an adjustment must be made:
Pages 60-61
A
18
Q
What are the effective interest rates of the following three banks?
- Bank A: 15% compounded daily
- Bank B: 15.5% compounded quarterly
- Bank C: 16% compounded annually
* Page 62*
A
19
Q
For a credit card that charges 1.6% per month, the effective annual rate will be:
Pages 62-63
A
20
Q
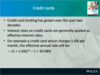
What is the net present value (NPV) formula?
Pages 65-66
A
The holy grail of finance!
NPV is the present value of the future cash flows minus your initial outlay (investment)
Cannot be treated as an annuity because each cash flow is different (an annuity is identical each year)
21
Q
How does the textbook define NPV?
What is missing in the definition?
Pages 65-66
A
- while the textbook covers the Sharpe ratio and the capital asset pricing model (CAPM), it doesn’t mention EMH
- if we don’t have efficient markets, the CAPM doesn’t work
a perfect market
- an infinite number of sellers and buyers
- everyone has perfect knowledge of the situation
- nobody can dominate the market
22
Q
What is an efficient market?
What are the 3 forms of EMH?
What is an inefficient market?
EMH supplementary material handout
A
Efficient market
- how accurately and how quickly the market translates new information into the share price
3 levels of efficiency
Strong-form: stock market where news is accurately interpreted and instantly feeds into share price (non-existent)
Semi-strong-form: you can beat the stock market index by having (illegal) insider information (New York)
Weak-form: insider information is still valuable, but you can also beat the market by applying fundamental analysis of the firms - performance, solvency, reading the accounts, understanding the economics, becoming informed about a company’s competitive position (Tokyo, Hong Kong, London, Sydney)
Inefficient market
- slow to adjust to news, or misinterprets it
- may not be enough traders to buy/sell shares, or cartels keeping up the price
(022)
23
Q
What is the weakness of the NPV technique?
Pages 65-66
A
- based on predictions
- predictions can be wrong - including the cost of capital (the discount rate itself)
- false security to rely exclusively on NPV when choosing between projects
24
Q
If an investment costs $300 today and is expected to return $100 at the end of the next 4 years with an interest rate of 10% p.a., then the NPV is calculated as:
Page 66
A
25
How do we calculate the present value (of future cash flow)?
## Footnote
*Page 66*
discount factor x future cash flow = present value
26
1. What is the internal rate of return (IRR)?
2. Who uses it?
* Pages 67-68*
1.
- the break-even cost of capital
- the discount rate that gives you an NPV of zero
- the maximum interest rate that a project can afford and still be profitable
2.
- the public sector: chooses projects before it chooses to finance
(will NOT be asked to calculate IRR)
27
What does it mean if the IRR is greater than the actual cost of capital?
Why would we need to calculate the IRR?
*Page 68*
- that is good!
- calculate the IRR if you really don't know how you're going to finance the project
28
What are some examples of fixed-interest securities?
What are they?
How do some types differ from others?
*Pages 68-70*
29
If the interest rates drop from 12% to 8%, what happens to the value of his investment?
## Footnote
*Pages 68-70*
30
How do you calculate the present value (PV) of future returns (FV)?
## Footnote
*Page 69*
31
Why has Howard's investment dropped from a value of $1,240 to just $1,072.60?
## Footnote
*Page 69*
*i* is now only 4% (rather than 6%) and the PV of future cash flows decrease
32
Both inflation and tax affect what of an investment?
## Footnote
*Page 71*
33
What is the effect of tax and inflation on the real rate of return?
## Footnote
*Page 71*
- interest is taxable
- if you also subtract the inflation rate, you are left with the real rate of return
real = after inflation
real rate = means having taken inflation into account
34
1. What is the economic interpretation of an NPV?
2. What effect would it have on a strong-form efficient market? A weak-form efficient market?
3. What is one of the reasons why NPV is so popular?
* Pages 65-66*
1. The economic interpretation of an NPV is the amount by which the firm's value will rise as a result of undertaking the project
2. In a strong-form efficient market, NPV would have a stock market effect; in a weak-form efficient market, it would have a very fuzzy one
3. One of the reasons why NPV is so popular is because the dominant school of thought in economics is still based on a strong-form efficient market
35
What is the general NPV rule regarding choosing between projects?
## Footnote
*Page 66*
36
What are the four personal wealth ratios?
## Footnote
*Page 49*
37
What is the difference between the compounding and discounting factor?
*Page 53*
38
What is the discount factor?
## Footnote
*Page 56*
39
What is an ordinary annuity?
*Page 57*
- a series of cash flows that are **identical** in amount and occur at the *end* of consecutive time periods
40
What is the formula for the effective interest rate?
## Footnote
*Page 60*
41
What does the IRR signify?
## Footnote
*Page 67*
- the break-even cost of capital
42
An investment providing a nominal interest rate of 6% p.a. compounded monthly is equivalent to an effective interest rate of:
Select one:
a. less than 6%
b. equal to 6%
c. more or less than 6% depending on the investment term
d. none of the above
**d.** none of the above
An effective interest rate will always exceed the nominal interest rate whenever there is more than a single compounding period per annum. In this situation where there is monthly compounding (hence there are 12 compounding periods per annum), the interest rate will be more than 6% p.a.
(Learning Objective 2.5 ~ understand the difference between nominal and effective interest rates)
43
An ordinary annuity is characterised by:
Select one:
a. a series of cash flows that are identical in amount and occur at the end of consecutive time periods.
b. a series of cash flows that are identical in amount and occur at the start of consecutive time periods
c. a single cash flow that occurs at the end of a particular time period and is accumulated over multiple time periods.
d. none of the above.
**a.** a series of cash flows that are identical in amount and occur at the end of consecutive time periods.
An ordinary annuity is characterised by a series of cash flows that are identical in amount and occur at the end of consecutive time periods.
(Learning Objective 2.4 ~ explain the concept of the time value of money and the benefits of compound interest)
44
Mr Rolf Weasley has recently purchased $12,000 worth of shares in Perloins Ltd. Given the relative risk exposure of Perloins Ltd., Rolf expects an annual rate of return on the investment of 9% p.a. compounded at regular intervals of 4 months. Approximately how much would Rolf expect to realise from the sale of his investment in 5 years from now?
Select one:
a. $18,696
b. $13,911
c. $43,710
d. $18,463
**a.** $18,696
The future value calculation can be made using the formula;
FV = PV(1 + *i*)n as follows:
FV = $12,000(1 + 3%)15
= $12,000(1.03)15 = $18,695.61
The future value of the investment at the end of 5 years is approximately $18,696.
(Learning Objective 2.4 ~ explain the concept of time value of money and the benefits of compound interest)
45
Approximately how much would you currently pay for an investment at a discount rate of 11% p.a. which produces an end of year cash inflow of $160 each year for 3 years?
Select one:
a. $391
b. $1,480
c. $369
d. $480
**a.** $391
The amount currently payable can be calculated using the present value formula; PV = (PMT[1 - (1 + i)-n]) / i as follows:
PV = ($160[1 – (1 + 11%)-3] / 11% = $390.99
The investor would be prepared to currently pay approximately $391 for the investment.
(Learning Objective 2.4 ~ explain the concept of the time value of money and the benefits of compound interest)
46
NPV is:
Select one:
a. the comparison of what is proposed to be outlaid or invested in today’s dollars with what the investment is predicted to return in today’s dollars.
b. the sum of the future value of cash inflows less cash outflows.
c. both a and b.
d. positive at all discount rates greater than the IRR.
**a.** the comparison of what is proposed to be outlaid or invested in today’s dollars with what the investment is predicted to return in today’s dollars.
47
A period of negative savings where income does not meet the required level of expenditures could also be regarded as a(n):
Select one:
a. asset.
b. increase in equity.
c. savings surplus.
d. savings deficit.
**d.** savings deficit.
A savings deficit is another term for a period of negative savings.
(Learning Objective 2.1 ~ prepare personal financial statements)
48
The relationship between the effects of taxation and positive rates of inflation on investment returns for a fixed interest security will be: *page 71*
Select one:
a. positive for both taxation and positive rates of inflation.
b. inverse for taxation and positive for positive rates of inflation.
c. inverse for both taxation and positive rates of inflation.
d. none of the above.
**c.** inverse for both taxation and positive rates of inflation.
Both taxation and positive rates of inflation are inversely related to investment returns for a fixed interest security as higher rates of each reduce the current value of such security.
(Learning Objective 2.7 ~ apply the time value of money concept to different investment choices)
49
A rational response in relation to an investment involving time preference for money issues is to prefer to receive a given sum of money earlier rather than later because:
Select one:
a. there is a greater chance that the entity promising you the money may not fulfil the promise the longer the waiting period.
b. the earlier the money is received the earlier the ability to reinvest and earn a rate of return on such funds.
c. the earlier the money is received the earlier the ability to use the funds for current consumption.
d. all of the above.
**d.** all of the above.
All of the factors mentioned are relevant in providing a rational response as to why an investor would prefer to receive a given sum of money earlier rather than later.
(Learning Objective 2.4 ~ explain the concept of the time value of money and the benefits of compound interest)
50
Technical insolvency occurs when a person or a company
Select one:
a. has run out of cash
b. cannot pay their debts on time
c. has more liabilities than assets
d. files for bankruptcy
**b.** cannot pay their debts on time
51
A loan is made to a borrower at a specified nominal interest rate. In order for the loan to be fully repaid over a specified term:
Select one:
a. periodic repayments would be the same whether they were made at the start or end of each period.
b. periodic repayments would be greater if they were made at the start rather than at the end of each period.
c. periodic repayments would be greater if they were made at the end rather than at the start of each period.
For the loan to be fully repaid over a specified number of repayments, the application of the time preference for money concept (where the preference is for earlier rather than later cash flows) would result in the conclusion that periodic repayments would need to be greater over a specified term if they were made at the end rather than at the start of each period. Learning Objective 2.5 ~ understand the difference between nominal and effective interest rates.
d. whether periodic repayments would be greater if they were made at the start or at the end of each period would depend on the specified interest rate.
**c.** periodic repayments would be greater if they were made at the end rather than at the start of each period.
For the loan to be fully repaid over a specified number of repayments, the application of the time preference for money concept (where the preference is for earlier rather than later cash flows) would result in the conclusion that periodic repayments would need to be greater over a specified term if they were made at the end rather than at the start of each period.
(Learning Objective 2.5 ~ understand the difference between nominal and effective interest rates)
52
The debt-service ratio shows monthly debt commitments as a percentage of:
Select one:
a. before-tax monthly income.
b. total liabilities.
c. after-tax monthly income.
d. none of the above.
**c.** after-tax monthly income.
The debt-service ratio expressed as a percentage is calculated as the monthly debt commitment divided by after-tax monthly income.
(Learning Objective 2.2 ~ understand the purpose of analysing financial statements using ratio analysis)
53
Mr & Mrs Kelso are seeking a loan to buy a caravan to use to travel around Australia. The on-road cost of the caravan is $35,000. The loan details they have been provided from Ezy Credit are that the interest rate charged will be 9% p.a. and require end-of-month repayments over a 4-year term. The initial fees that form part of the loan arrangement are an establishment fee of $750 as well as a brokerage fee to Ezy Credit calculated as 2% of the loan value. Given that Mr & Mrs Kelso wish to borrow all the funds required to obtain the caravan what will be the approximate end-of-month loan repayment? *Page 225*
Select one:
a. $894.60
b. $938.35
c. $612.80
d. $907.80
**d.** $907.80
We initially need to determine the loan amount which will be $35,000 plus the relevant fees. Hence we know that $35,750 will provide Mr & Mrs Kelso with 98% of the total loan value (given a brokerage fee of 2% to Ezy Credit) which can be shown as follows:
98% (loan) = $35,750
Loan = $35,750 / 98% = $36,480
Now that we know the total loan value required ($36,480) we can calculate the monthly loan repayment using the formula:
PV = PMT [1 – (1 + i)-n] / i
$36,480 = PMT [1 – (1 + (9%/12)-48] / (9%/12)
$36,480 = PMT [1 – (1 + (0.0075)-48] / (0.0075)
$36,480 = PMT [1 – (1 + (0.0075)-48] / (0.0075)
$36,480 = PMT (0.3014] / (0.0075)
PMT = $36,480 / 40.1848
= $907.80
(Learning Objective 2.4 ~ explain the concept of time value of money and the benefits of compound interest)
54
The greater the initial investment the:
Select one:
a. greater the future value at a given interest rate and given number of periods.
b. lower the future value at a given interest rate and given number of periods.
c. future value will be the same at a given interest rate and given number of periods.
d. none of the above.
**a.** greater the future value at a given interest rate and given number of periods.
The greater the initial investment the greater the future value at a given interest rate and given number of periods. This follows from the future value equation; FV = PV(1 + i)n . (Learning Objective 2.4 ~ explain the concept of time value of money and the benefits of compound interest)
55
Which of the following is generally true about the calculation of an individual’s equity or net worth ratio?
Select one:
a. For a young person or couple, it is expected that their equity ratio would be relatively low as they are likely to have a relatively high level of debt.
b. For a young person or couple, it is expected that their equity ratio would be relatively high as they are likely to have a relatively low level of debt.
c. The ratio shows the percentage of net worth to total assets.
d. Both a and c.
**d.** Both a and c.
The equity/net worth ratio is the ratio of net worth to total assets, expressed as a percentage and for a young person or couple, it is expected that their equity ratio would be relatively low as they are likely to have a relatively high level of debt.
(Learning Objective 2.2 ~ understand the purpose of analysing financial statements using ratio analysis)
56
The NPV of an investment requiring an initial outlay of $10,000 at a discount rate of 6% which provides end-of-year cash flows of; year 1 - $3,000 (inflow), year 2 - $11,000 (inflow), year 3 - $1,500 (outflow) and year 4 - $7,000 (inflow) will be approximately:
Select one:
a. $9,424.
b. $6,163.
c. $19,500.
d. $6,905.
**d.** $6,905.
We can calculate the NPV as follows:
NPV = -$10,000 + $3,000 / (1 + 6%)1 + $11,000 / (1 + 6%)2 - $1,500 / (1 + 6%)3 + $7,000 / (1 + 6%)4
= -$10,000 + ($3,000 / 1.06) + ($11,000 / 1.1236) - ($1,500 / 1.191) + ($7,000 / 1.2625)
= -$10,000 + $2,830 + $9,789 - $1,259 + $5,545
57
If you were to deposit $850 today into an investment account earning 6% p.a. compounded annually, approximately how much will you have in your account at the end of 5 years?
Select one:
a. $1,165
b. $620
c. $1,206
d. $1,137
**d.** $1,137
The future value calculation can be made using the formula;
FV = PV(1 + i)n as follows:
FV = $850(1 + 6%)5 = $850(1.06)5 = $1,137.49
The future value of the investment at the end of 5 years is approximately $1,137.
(Learning Objective 2.4 ~ explain the concept of time value of money and the benefits of compound interest)
58
A personal balance sheet would not generally include:
Select one:
a. dividends received during a period.
b. a motor vehicle.
c. a collection of rare banknotes.
d. both a and b.
**a.** dividends received during a period.
Dividends received during a period should be included in the personal cash flow statement, not the personal balance sheet.
(Learning Objective 2.1 ~ prepare personal financial statements)
59
Which of the following items would not generally be included in the calculation of an individual’s liquidity ratio?
Select one:
a. the total outstanding balance of a 25-year mortgage loan taken out in the last year
b. debt repayments over the next 12 months
c. amount of an outstanding telephone account
d. both a and c
**a.** the total outstanding balance of a 25-year mortgage loan taken out in the last year
The liquidity ratio includes the amount of debt which is to be repaid within the next 12 months and hence would not include the total outstanding balance of a mortgage loan with a remaining term of more than 12 months.
(Learning Objective 2.2 ~ understand the purpose of analysing financial statements using ratio analysis)
60
An investor is seeking to make an investment decision over a 4-year term between alternative fixed interest securities of equivalent risk with each providing accumulated interest amounts on maturity. The ABC security offers a fixed interest rate of 8% for a 3-year maturity whereas the XYX security offers a fixed interest rate of 9% for a 4-year maturity. What initial calculation should be the basis for the decision-making between the securities?
Select one:
a. to calculate a forward rate for year 4 of the XYX security
b. to calculate a forward rate for year 4 of the ABC security
c. to calculate a forward rate for year 3 of the ABC security
d. none of the above
**b.** to calculate a forward rate for year 4 of the ABC security
To resolve the decision-making dilemma between securities ABC and XYX we can solve for the rate at which the 4th year of security ABC is expected to represent the same financial outcome as for security XYX. This is known as the forward rate.
(Learning Objective 2.7 ~ apply the time value of money concept to different investment choices)
61
In the calculation of the savings ratio, savings is defined as:
Select one:
a. the amount left over after deducting all expenditures from income.
b. the balance of an individual’s funds on deposit at a bank at the end of a period.
c. the amount left over after deducting expenditure from income after we add back items that may be regarded as an investment.
d. both a and b.
**c.** the amount left over after deducting expenditure from income after we add back items that may be regarded as an investment.
Savings, as defined in the savings ratio, is the amount left over after deducting expenditure from income after we add back items that may be regarded as an investment.
(Learning Objective 2.2 ~ understand the purpose of analysing financial statements using ratio analysis)
62
Explain in your own words why $100 today will buy more goods and services than $100 in 3 years.
The difference in value is attributed to the effect of inflation, which erodes the value of $1 at today’s prices.
A participant also mentioned that money available today can be invested for future returns, which are lost from the current consumption of the money.
63
An advertisement offers a fixed term deposit for 4 years with an interest rate of 4.8% p.a. compounded annually or a fixed deposit for 4 years with an interest rate of 4.65% p.a. compounded quarterly. Which one would you choose? Explain why.
This involves working out the future value for each option. A decision can be arrived at by considering the compounding factors. That is (1+0.048)^4 and (1+0.0465/4)^16
Note that the interest rate for compounding or discounting is expressed as an annual rate. Where payments/receipts occur more frequently than on an annual basis than the rate per period has to be used in the calculation. Where payments/receipts are made half-yearly the annual interest rate is divided by 2; where payments/receipts are quarterly the annual interest rate is divided by 4; and by 12 where payments/receipts are monthly. To illustrate the answer to the question, it is assumed the amount of the fixed term deposit is $1000.
Marginally, you would choose Option 1 because it provides a slightly higher return over the 4 years. The difference is a little over $3.00. A participant noted that the difference will be higher if the amount invested is larger.
64
(a) A credit card is a virtual requirement in today’s society. Do you agree or disagree with this statement? Explain.
(b) Find out the nominal interest rate on your own credit card and calculate the effective rate of interest.
The answer depends on the opinion. This was discussed with a number of different opinions. It was mentioned that debit cards are used more often these days than credit cards. I added that credit cards can be handy for paying for things we want or have to pay for (e.g. electricity) when we don’t have our own money. Provided well managed, credit cards can be a good source of cash. On the other hand, if balances on a credit card account are not well managed, interest and fee payments can be high. A participant suggested that credit cards are good for business rather than for individuals.
It was agreed that the effective interest rate will be higher than the nominal rate (annual rate) where payments are made monthly.
65
Your uncle invested $50 000 in a 5-year fixed-term security 2 years ago when the interest rate was 5.5% p.a. payable half-yearly. He now needs to get his money back as an emergency situation has arisen. He asks a broker to sell the security on the securities exchange market and is delighted to receive the sum of $53 000. Explain why your uncle has received more than he originally invested.
66
Brad and Nerida are considering two alternative investments.
Option 1 requires an outlay of $10 000 and from the end of the 2nd year is expected to bring a cash flow of $1500 p.a. for the next 3 years. Then the investment would be terminated and they would get their $10 000 back.
Option 2 requires an outlay of $15 000 and is expected to bring a cash flow of $1200 for each of the next 5 years. They would then expect to sell the investment for $17 500.
Explain how net present value calculations would help them to decide on the best investment choice.
NPV is the sum of the present value of cash inflows less cash outflows and is a means to determine whether an investment is worth undertaking. The NPV technique is widely used to compare and evaluate investment options for investors.
Net present value is calculated as follows:
NPV = PV (Future cash flows) - Investment today
The process of discounting the expected future cash inflows (to give a present value) is based on the reverse of compounding.
**Option 1**
NPV = -10,000 + 0/(1+0.1)1 + 1,500/(1+0.1)2 + 1,500/(1+0.1)3 + 11,500/(1+0.1)4
= -10,000 + 0 + 1,239.67 + 1,126.97 + 7,854.65 = $221.29
**Option 2**
NPV = -15,000 + 1,200/(1+0.1)1 + 1,200/(1+0.1)2 + 1,200/(1+0.1)3 + 1,200/(1+0.1)4 + 18,700/(1+0.1)5
-15,000 + 1,090.91 + 991.74 + 901.58 + 819.62 + 11,611.22 = $415.08
For Brad and Nerida to decide on the two alternatives they need to consider the NPV of the two proposals. The key deciding factor will be the rate of return that they expect or hope to achieve from the two alternatives. To conduct an NPV they should undertake their calculations with their desired rate of return and choose the highest NPV of the two choices. Assume a desired rate of return of 10%
67
Cherie, one of your clients, invested $50 000 into a fixed-term security at a rate of 6% p.a. Cherie earns income that puts her in the 34% marginal tax bracket. She wonders why you have mentioned that she needs to understand the effects of inflation and taxation on her ‘real’ rate of return. Calculate the real rate of return to Cherie if inflation is given as 3% and write a brief explanation to Cherie to demonstrate the real rate of return on her investment.
Cherie’s real rate of return is eroded by her high marginal tax rate and by the inflation rate of 3 cents in the dollar.
68
Angie has received an offer in the mail to transfer her $5,000 credit card balance to a new provider. The offer is ‘low rate and no fees’. The rate offered is 3.99% p.a. compounded monthly for 6 months with no application fees or transaction fees. However, in the terms and conditions it says:
* after the 6-month introductory period, the interest rate will revert to 19.5% p.a., which is a variable rate
* the transferred balance will be repaid first
* note that the effective interest for 19.5% paid monthly is ((1+0.195/12)12) – 1 = 21.34%
* government charges and a late payment fee may apply
* minimum monthly repayments are required to be 3% of the outstanding loan amount or $30, whichever is the greater
a. What advice can you give Angie?
b. Why might Angie consider switching to the new provider?
a.
* Angie needs to pay the balance of her credit card owing before the 6 month period expires otherwise her effective interest rate could be much higher
* Any new purchase she makes may increase the effective interest rate she pays
* Government charges and late fees are potential additional costs she will incur
* She must have sufficient cash available to pay the minimum amount due each month
b.
If she can meet the rules of the new credit card arrangement, in the long-run she may save money by reducing her repayment costs.
