Trigonometry Flashcards
(54 cards)
State the three basic Trigonometric identities.

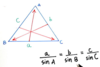
State the sine rule
Draw the cast diagram for degrees (including both positive and negative angles)
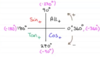
State the Cosine Rule
The cosine rule is as follows:
a2 = b2 + c2 - 2bc cosA
or
b2 = a2 + c2 - 2bc cosB
or
c2 = a2 + b2 - 2bc cosC
How do you convert degrees to radians?
Given that 1º = πc/180
to convert ‘n’ degrees to ‘rad’ multiply ‘n’ as follows:
nº x πc/180º = nπc/180
How do you convert from Radians to Degrees?
Given that 1c = 180º/π
to convert ‘n’ radians to degrees multiply ‘n’ as follows:
nc x 180º/πc = 180nº/π
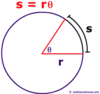
How can you determine the length of an arc using radius length and angle in radians?
Given an angle of radians you can use the following formula:
s = rØ
note: the units of the arc length will be the same as those of the radius.
How can you determine the Area of a Sector given a radius and an angle in Radians?
Given a radius and and angle in radians the area of a sector can be determined using the following equation:
A = ½r2Ø
note: the units of the area are equal to those of the radius squared.

How can you determine the area of a sector given a radius and an angle in degrees?
Given a radius and and angle in degrees the area of a sector can be determined using the following equation:
A = Ø/360 • πr2
note: the units of the area are equal to those of the radius squared.

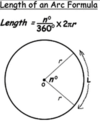
How can you determine the length of an arc using radius length and an angle in degrees?
Given an angle of degrees you can use the following formula:
s = Ø/360 • 2πr
note: the units of the arc length will be the same as those of the radius.
Given a radius and an angle in radians, how can you calculate the area of a segment?
Given that the Area of a Sector is ½r2Ø, Ø in radians
and the Area of the Triangle is ½r2 SinØ
The Area of the Segment = ½r2Ø - ½r2 SinØ
= ½r2(Ø - SinØ)
Given a radius and an angle in Degrees, how can you determine the Area of a Segment?
Given that the Area of a Sector is Ø/360•πr2, Ø in degrees
and the Area of the Triangle is ½r2 SinØ
The Area of the Segment = Ø/360•πr2 - ½r2 SinØ
= ½r2(Øπ/180 - SinØ)
What are the three basic reciprocal trigonometric identities and there definitions?
Sec x = 1/Cos x (The secant function)
Cosec x = 1/Sin x (The cosecant function)
Cot x = 1/Tan x (The cotangent function)
What are the three Triangle Trig Identities and their variations?
Hint: the first is equal to 1, and the others are derived from it.
sin2x + cos2x = 1
var1 : 1 - sin2x = cos2x
var2 : 1 - cos2x = sin2x
1 + tan2x = sec2x
var1 : tan2x = sec2x - 1
var2 : 1 = sec2x - tan2x
1 + cot2x = cosec2x
var1 : cot2x = cosec2x - 1
var2 : 1 = cosec2x - cot2x
What are the Sine Compound-Angle Forulae?
Sin(x + y) = Sin(x) Cos(y) + Cos(x) Sin(y)
Sin(x - y) = Sin(x) Cos(y) - Cos(x) Sin(y)
What are the Cosine Compound-Angle Formulae?
Cos(x + y) = Cos(x) Cos(y) - Sin(x) Sin(y)
Cos(x - y) = Cos(x) Cos(y) + Sin(x) Sin(y)
What are the Tangent Compound-Angle Formulae?
Tan(x + y) = [Tan(x) + Tan(y)] / [1 - Tan(x) Tan(y)]
Tan(x - y) = [Tan(x) - Tan(y)] / [1 + Tan(x) Tan(y)]
What are the Double-Angle Formulae?
Sin 2x = 2 Sinx Cosx
Cos 2x = Cos2x - Sin2x
= 2 Cos2x - 1
= 1 - 2 Sin2x
Tan 2x = [2 Tanx] / [1 - Tan2x]
What is the ratio of Sin 30º?
Sin 30º = ½
What is arcsin (½) in degrees?
sin-1 (½) = 30º
What is the ratio of sin π/6?
sin π/6 = ½
What is the arcsin (½) in radians?
sin-1 (½) = π/6
What is the ratio of sin (45º)?
sin (45º) = 1/√2
= √2/2
What is arcsin (√2/2)?
sin-1 (√2/2) = 45º


