10 - Strings and Text 1

Question 1

What is the terminology for this topic?

Answer 1

an alphabet = {A, C, G, T} (DNA)

= ASCII, Unicode, etc

a string = ACAGTCCGGGACT

all strings indexed from position 1

Let S,T be two strings

|S| is length of S

S(i) is indexing S S(i .. j) denotes S(i)S(i+1) ..

S(j) ST is concatenation of S and T

Question 2

What is a substring?

Answer 2

ACAGTCCGGGACTGACG

a string contained within a string a substring of S is S(i .. j) (i

Question 3

What is a common substring?

Answer 3

TCCACTGACTGCTGC

ACAGTCCGGGACTGACG

GACTG is a common substring U is a common substring of S and T if U is a substring of both S and T

Question 4

What is a subsequence?

Answer 4

ACAGTCCGGGACTGACG

obtained by deleting 0 or more characters from the string

Question 5

What is a common subsequence?

Answer 5

ACAGTCCGGGACTGACG

TCCACTGACTGCTGC

U is a common subsequence of S and T if U is a subsequence of both S and T

Question 6

What is a prefix?

Answer 6

ACAGTCCGGGACTGACG

S(1 . . k) for some k (1 k n), where n = |S|

Question 7

What is a suffix?

Answer 7

ACAGTCCGGGACTGACG

S(k . . n) for some k (1 k n), where n = |S|

Question 8

What is star / *?

Answer 8

* = {,A,C,G,T,AA,AC,AG,AT,CA,…}

set of all strings composed of symbols from the alphabet

Question 9

What is the leaf terminology?

Answer 9

a leaf node: no children

a branch node: 1 or more children

a unary node: exactly 1 child

a binary node: exactly 2 children

Question 10

What is the naive solution to finding longest repeated substring?

Answer 10

• String S of length n, build n x n array A with A(i, j) = 1 if S(i) = S(j) and A(i, j) = 0 otherwise
• repeated substrings are represnted by sequences of 1’s on a diagonal
• scan all diagonals to find longest repeat
• O(n²) time and space
• repeated substrings may overlap

Question 11

What is naive solution to common substrings?

Answer 11

• Find longest common substring of two strings
• two strings S, T of lengths m, n
  
  • build similar m x n array of 0’s and 1’s
  • gives longest common substring of T and S in O(mn) time and space

Question 12

Using trees for suffixes

Answer 12

• Let S be string of length n
  
  • k^th suffix of S is the suffix S(k..n)
  • S has n suffixes, including S itself
• Data structures to store the n suffixes of S
  
  • Suffix Trie - O(n²) space
  • Suffix Tree - O(n) space

Question 13

What problems use a suffix tree to solve them?

Answer 13

• Longest repeat of S
  
  • O(n) time/spacespace
• Longest common substring
  
  • O(m+n) time/space for 2 strings S,T where m = |S| and n = |T|
• Multiple string searching
  
  • O(n+r) time/space, for long peice of text T (n = |T|) and strings of total length r

Question 14

What is a Suffix Trie?

Answer 14

• A trie is a multiway branching tree T
  
  • used to store strings C over an alphabet Σ

Question 15

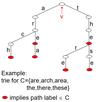
What are the properties of a Suffix Trie?

Answer 15

• suffix trie T for string S is a trie used to store all suffixes of S
• T is rooted at some vertex v
• Each edge of T is labelled with some σ∈Σ
• No 2 children of a node have same edge label
• Each node w corresponds to a string S∈Σ* (concatentation of edge labels on the path from v to w) - S is the path label of w
• Each node is marked according to whether ir corresponds to a string S∈C
• each suffix of S represented by unique leaf node of T
• if some suffix of S is a prefix of another suffix
  
  • then a suffix trie for S may not exist, e.g. consider S = queue
• can ensure the suffix trie exists by appending to s a character $ not appearing in S, before constructing T

Question 16

Example of suffix trie

Answer 16

see slides

lecture 10 slide 11/14

Question 17

Building a suffix trie

Answer 17

• Inserting i^th suffix takes O(n-i) steps
  
  • so requires O(n²) time overall
• How many nodes?
  
  • text length n, typically proportional to n2
  • space needed is quadratic in n
• Searching for string length m is O(m) after O(n²) preprocessing time
• Finding longest repeat is O(n²)
• In both cases O(n²) space needed
• Can we improve?
  
  • Yes - suffix tree