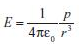Chapter 6: Electrostatics Flashcards
Electrostatics is:
the study of stationary charges and the forces that are created by and act upon these charges
Proton charge:
positive
Electron charge:
negative
Opposite charges exert what kind of forces?
attractive
Like charges exert what kind of forces?
repulsive
The SI unit of charge is the:
Coulomb [C]
The fundamental unit of charge (e) is:
e = 1.6 X 10-19 Coulombs
The charge of one proton and the charge of one electron are equal to:
1.6 X 10-19 Coulombs; protons are positive, electrons are negative
Coulomb’s law gives us:
The magnitude of the electrostatic force F between two charges q1 and q2 whose centers are separated by a distance r.
The equation used to determine the attractive or repulsive force two charges exert on one another:
F = kq1q2 / r2;
where k = 8.99 X 109 NM2/C2; q1 and q2 are in Coulombs; r is in meters
The direction of the force between two charges may be obtained by remembering that:
like forces repel and opposite forces attract
An electric field is:
the electrical force on a stationary positive charge divided by the charge
Electric fields are produced by:
a stationary source charge (q)
A stationary test charge is:
the charge placed in the electric field
Whether the force exerted through the electric field is attractive or repulsive depends on:
whether the stationary test charge and the stationary source charge are opposite or like charges
The equation used to determine the electric field produced by a source charge at a chosen point in space:
E = F/q0 = Kq/r2;
where E is the electric field magnitude, F is the force felt by the test charge q0, k is the electrostatic constant (8.99 X 109), q is the source charge magnitude, and r is the distance between the charges.
E = F/q0 requires:
the presence of the test charge in the electric field
E = kq/r2 does not require:
the presence of a test charge in the electric field
The direction of the electric field vector is given as:
the direction a positive test charge (+q0) would move in the presence of the source charge. If the source charge is positive, the electric field vector radiates outwards. If the source charge is negative, the electric field vector radiates inwards.
A collection of charges in an electric field will exert a net electric field at a point in space that is equal to:
the vector sum of all three of the electric fields
The equation used to determine the total electric field at a chosen point in space:
Etotal = Eq1 + Eq2 + Eq3 + …
The magnitude of the force exerted on a test charge place in an electric field can be calculated using the equation:
F = q0E; where q0 is the charge of the test charge and E is the magnitude of the electric field
Electric potential energy is:
the potential energy related to the relative position of one charge with respect to another charge or to a collection of charges. It is the work necessary to move a test charge from infinity to a point in space in an electric field surrounding a source charge.
The equation used to calculate the electric potential energy between two charges separated in space:
U = kqQ / r
where k = 8.99 X 109, q is one charge, Q is a second charge, and r is the distance between them
Electric potential energy is positive when:
the charges are like charges
Electric potential energy is negative when:
the charge are opposite charges
When unlike charges move towards each other, the electric potential energy:
decreases
When unlike charges move apart from one another, the electric potential energy:
increases
The electrical potential energy (U) is equal to:
the work (W) necessary to move a test charge from infinity to a point in space in an electric field surrounding the source charge.
Electric potential is:
the ratio of the magnitude of a charge’s potential energy (U, which is equal to W) divided by the magnitude of the test charge itself. It is the electric potential energy per unit of charge
The equation used to determine the electric potential due to a known source charge at a chosen point in space is:
V = W / q0 = kQ/r
where V is he electric potential measured in volts, W is the electric potential energy of the charge, q0 is the charge of the test charge, and Q is the magnitude of the source charge.
1 Volte is equal to:
1 Joule / Coulomb
Electric potential is a:
scalar quantity
For a collection of charges, the total electric potential at a point in space is:
the scalar sum of the electric potential due to each charge (Vtotal = Vq1 + Vq2 + Vq3 + scalar sum)
The equation used to determine the potential difference between two points in space:
Vb - Va = Wab/q0
where Wab is the work needed to move a test charge q0 through an electric field from point a to point b.
Positive charges move spontaneously from:
high voltage to low voltage
Negative charges move spontaneously from:
low voltage to high voltage
The equipotential line is the one in which:
the potential at every point is the same (the potential difference between any two points on the equipotential line is zero)
Work needed to move a test charge from point a to point b through an electric field depends only on:
the the potential difference; the path taken is negligible and does not matter
The electric dipole results from:
two equal and opposite charges being separated a small distance from each other
The equation used to determine the electric potential at a point in space due to an electric dipole:
V = (kp/r2)cosØ
where p is the dipole moment, r is the distance between the point in space and the midpoint of the dipole, and theta is the angle between r and the dipole
The equation used to determine the electric field due to an electric dipole along the perpendicular bisector of the dipole:
The equation used to determine the net torque experienced by an electric dipole about the center of the dipole axis due to an external electric field:
t = pE(sinØ)
where p is the magnitude of the dipole moment, E is the magnitude of the electric potential, and Ø is the angle the dipole moment makes with the electric field
The magnitude of the dipole moment (p) is equal to:
p = qd
The torque place on a dipole will cause the dipole to:
reorient itself by rotating so that its dipole moment (p) aligns with the electric field (E)
In an external electric field, an electric dipole will experience a net torque until:
it is aligned with the electric field vector
An electric field will not induce any translational motion regardless of:
its orientation with respect to the electric field vector.
