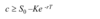Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Finance > Financial Engineering > Flashcards

Financial Engineering Flashcards

You may prefer our related Brainscape-certified flashcards:
Series 65 flashcards Series 63 flashcards Series 66 flashcards Series 7 Top-off Exam flashcards SIE Exam flashcards CFA flashcards Series 79 Top-Off Exam flashcards
1
Q

Optimal Hedge Ratio

A

(Page 57)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Basis Risk

A
  • Basis is usually defined as the spot price minus the futures price
  • Basis risk arises because of the uncertainty about the basis when the hedge is closed out
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Measuring Interest Rates

A

•When we compound m times per year at rate R an amount A grows to A(1+R/m)m in one year

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Continuous Compounding formula etc.

A
  • In the limit as we compound more and more frequently we obtain continuously compounded interest rates
  • $100 grows to $100eRT when invested at a continuously compounded rate R for time T
  • $100 received at time T discounts to $100e-RT at time zero when the continuously compounded discount rate is R
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Contiuous Compounding Conversion formulas

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

If the spot price of an investment asset is S0 and the futures price for a contract deliverable in T years is F0, then….

A

F0 = S0erT

where r is the T-year risk-free rate of interest.

In our examples, S0 =40, T=0.25, and r=0.05 so that

F0 = 40e0.05×0.25 = 40.50

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Forward price when an Investment Asset Provides a known Yield/Return

A

F0 = S0 e<em>(r–q )T</em>

where q is the average yield during the life of the contract (expressed with continuous compounding)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

The value of a Forward Contract

A

•A forward contract is worth zero (except for bid-offer spread effects) when it is first negotiated
•Later it may have a positive or negative value
•Suppose that K is the delivery price and F0 is the forward price for a contract that would be negotiated today
•By considering the difference between a contract with delivery price K and a contract with forward price F0 we can deduce that:
–the value of a long forward contract, ƒ, is

    *(F<sub>0</sub> – K )e<sup>–rT</sup> *        –the value of a short forward contract is

(K – F0 )e–rT

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Forward vs Futures Prices

A

•When the maturity and asset price are the same, forward and futures prices are usually assumed to be equal.
•
•When interest rates are uncertain they are, in theory, slightly different:
–A strong positive correlation between interest rates and the asset price implies the futures price is slightly higher than the forward price
–A strong negative correlation implies the reverse

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Forward Stock Index Pricing

A
  • Can be viewed as an investment asset paying a dividend yield
  • The futures price and spot price relationship is therefore

F0 = S0 e<em>(r–q )T</em>

where q is the average dividend yield on the portfolio represented by the index during life of contract

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Index Arbitrage

A
  • When F0 > S0<em>e(r-q)T</em> an arbitrageur buys the stocks underlying the index and sells futures
  • When F0 < S0e(r-q)T an arbitrageur buys futures and shorts or sells the stocks underlying the index
  • Index arbitrage involves simultaneous trades in futures and many different stocks
  • Very often a computer is used to generate the trades
  • Occasionally simultaneous trades are not possible and the theoretical no-arbitrage relationship between F0 and S0 does not hold (19 October 1987)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Futures and Forwards on Currencies

A
  • A foreign currency is analogous to a security providing a yield
  • The yield is the foreign risk-free interest rate
  • It follows that if rf is the foreign risk-free interest rate

F0=S0e(r-rf)T

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Consumption Assets Formula

A

Storage is Negative Income

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

The Cost of Carry

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Valuation of an Interest Rate Swap

A
  • Initially interest rate swaps are worth close to zero
  • At later times they can be valued as the difference between the value of a fixed-rate bond and the value of a floating-rate bond
  • Alternatively, they can be valued as a portfolio of forward rate agreements (FRAs)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

The Put-Call Parity

A
  • Both are worth max(ST , K ) at the maturity of the options
  • They must therefore be worth the same today. This means that

c + Ke -rT = p + S0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Reasons For Not Exercising a Call Early (No Dividends)

A
  • No income is sacrificed
  • You delay paying the strike price
  • Holding the call provides insurance against stock price falling below strike price
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q
A

Bull Spread Using Calls

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q
A

Bull Spread Using Puts

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q
A

Bear Spread Using Puts
Figure 11.4, page 240

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q
A

Bear Spread Using Calls
Figure 11.5, page 241

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

What is a Box Spread?

A
  • A combination of a bull call spread and a bear put spread
  • If all options are European a box spread is worth the present value of the difference between the strike prices
  • If they are American this is not necessarily so (see Business Snapshot 11.1)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q
A

Butterfly Spread Using Calls
Figure 11.6, page 242

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q
A

Butterfly Spread Using Puts
Figure 11.7, page 243

25
Q
A

Calendar Spread Using Calls
Figure 11.8, page 245

26
Q
A

Calendar Spread Using Puts
Figure 11.9, page 246

27
Q
A

A Straddle Combination
Figure 11.10, page 246

28
Q
A

Strip & Strap
Figure 11.11, page 248

29
Q
A

A Strangle Combination
Figure 11.12, page 249

30
Q

FIX FORMULAS FOR BINOMIAL TREE

A

LECTURE 5

31
Q

Binomial Tree

u

d

A
32
Q

Binomial Tree

probability of an up move formula

A
33
Q

Stochastic Processes

A
  • Describes the way in which a variable such as a stock price, exchange rate or interest rate changes through time
  • Incorporates uncertainties
34
Q

Markov Processes (See pages 280-81)

A
  • In a Markov process future movements in a variable depend only on where we are, not the history of how we got to where we are
  • Is the process followed by the temperature at a certain place Markov?
  • We assume that stock prices follow Markov processes
  • In Markov processes changes in successive periods of time are independent
  • This means that variances are additive
  • Standard deviations are not additive
35
Q

Weak-Form Market Efficiency

A
  • This asserts that it is impossible to produce consistently superior returns with a trading rule based on the past history of stock prices. In other words technical analysis does not work.
  • A Markov process for stock prices is consistent with weak-form market efficiency
36
Q

Black Scholes Call Option Formula

A

C = *S0 N *(d1) - K e-rTN(d2)

37
Q

Black Scholes Put Option Formula

A

p = *K e-rT N (-d2*) - S0N(-d1)

38
Q

Black Scholes d1 and d2

A
39
Q

What is implied volatility?

A

The implied volatility is the volatility that makes the Black–Scholes-Merton price of an option equal to its market price. It is calculated using an iterative procedure.

40
Q

Theta

A

—Theta of a derivative (or portfolio of derivatives) is the rate of change of the value with respect to the passage of time

—The theta of a call or put is usually negative. This means that, if time passes with the price of the underlying asset and its volatility remaining the same, the value of a long call or put option declines

41
Q

Gamma

A
  • Gamma (G) is the rate of change of delta (D) with respect to the price of the underlying asset
  • Gamma is greatest for options that are close to the money
42
Q

Delta

A

•Delta (D) is the rate of change of the option price with respect to the underlying

43
Q

Delta Hedging

A
  • This involves maintaining a delta neutral portfolio
  • The delta of a European call on a non-dividend paying stock is N (d 1)
  • The delta of a European put on the stock is
44
Q

Vega

A

•Vega (v) is the rate of change of the value of a derivatives portfolio with respect to volatility

45
Q

Managing Delta, Gamma, & Vega

A
  • Delta can be changed by taking a position in the underlying asset
  • To adjust gamma and vega it is necessary to take a position in an option or other derivative
46
Q

Rho

A

Rho is the rate of change of the value of a derivative with respect to the interest rate

47
Q

All formulas for

Delta, Gamma, Theta, Vega, Rho

A
48
Q

Lower Bound for European Call Option Prices; No Dividends (Equation 10.4, page 220)

A
49
Q

Put-Call parity with dividend

A

c + Ke-rT+D = p + S0

50
Q

What is implied volatility? How can it be calculated?

A

The implied volatility is the volatility that makes the Black–Scholes-Merton price of an option equal to its market price. It is calculated using an iterative procedure.

51
Q

The Lognormal Property

A

•Since the logarithm of ST is normal, ST is lognormally distributed

52
Q

N’(d1) (N Prime) formula

A
53
Q

Hedge BEta

A

To hedge the risk in a portfolio the number of contracts that should be shorted is

[image]

where VA is the value of the portfolio, B is its beta, and VF is the value of one futures contract.

(Gamla B - Nya B) om nya aer mindre.

54
Q

Put-Call Parity - Market to BS

A
55
Q

Daily Volatilities

A
  • In option pricing we measure volatility “per year”
  • In VaR calculations we measure volatility “per day”
  • Theoretically, sday is the standard deviation of the continuously compounded return in one day
  • In practice we assume that it is the standard deviation of the percentage change in one day
56
Q

Standard Deviation of Portfolio

A
57
Q

The Linear Model and Options

A

Consider a portfolio of options dependent on a single stock price, S. If d is the delta of the option, then it is approximately true that

58
Q

Quadratic Model

A

Finance (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions