Konkrete Wahrscheinlichkeitsverteilungen: Binomialverteilung

Question 1

Vorbereitung I: Definition Fakultät, Binomialkoeffizient

Answer 1

• Def. Fakultät n! einer natürlichen Zahl n∈ℕ: Produkt der ganzen Zahlen von 1 bis n; per Definition: 0!=1
• Def. Binomialkoeffizient für k,n ∈ℕ, n>k:

Question 2

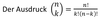
Vorbereitung II: Definition Unabhängigkeit von Zufallsvariablen

Answer 2

Genaue Def. formal sehr aufwendig

→ Intuitive Definition: Zwei ZV X und Y sind unabhängig, falls die Realisation der ZV X keine Auswirkung darauf hat, wie die ZV Y sich realisiert, und umgekehrt

Question 3

Herleitung Wahrscheinlichkeitsfunktion d. Binomialverteilung (Summen von unabhängigen Bernoulli-Variablen)

Answer 3

• Wir betrachten n unabhängige Bernoulli-Variablen X₁, X₂, … X_n mit X_i~Be(p) für alle i= 1, 2, … n (folgen alle einer Bernoulli-Verteilung m. dem selben p und sind unabhängig)
• →Summe dieser n Bernoulli-Variablen X=Σ ⁿ_{i<span> </span>=1} X_i wieder eine Zufallsvariable:
• X steht für die Anzahl der Bernoulli-Variablen, die sich bei n Durchgängen in dem Wert 1 realisiert haben (da sich die einzelnen Bernoulli-Variablen X_i nur i. d. Werten 0 oder 1 realisieren können)

→X kann Werte von 0 bis n annehmen: T_x={0, 1, 2, … n)

⇒Wahrscheinlichkeitsfunktion der ZV X (Summe n unabhängiger Bernoulli-Variablen)= Wahrscheinlichkeitsfunktion der Bernoulliverteilung:

Question 4

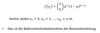
Definition Binomialverteilung

Answer 4

Eine ZV folgt einer Binomialverteilung, falls ihr Träger T_x={0,1,2, … n} ist, und ihre Wahrscheinlichkeitsfunktion die Form

Question 5

Binomialverteilung Verteilungsfunktion

Answer 5

• Erinnerung Zusammenhang Wahrscheinlichkeitsdichtefunktion und Verteilungsfunktion bei diskreten ZV
• Verteilungsfunktion einer binomialverteilten ZV X:

Question 6

Interpretation n und p

Answer 6

• n: Anzahl der zugrundeliegenden Bernoulli-Variablen
• p: Wahrscheinlichkeit für “Erfolg” der zugrundeliegende Bernoulli-Variablen Xi

Question 7

Biomialverteilung Erwartungswert

Answer 7

Ergibt sich aus den Erwartungswerten der eizelnen Bernoulli-Variablen X_i:

Question 8

Zusätzl. Rechenregeln Varianz

(unabhängige ZV)

Answer 8

Question 9

Binomialverteilung Varianz

Answer 9

Die Varianz ergibt sich aus den Varianzen der einzelnen Bernoulli-Variablen und deren Unabhängigkeit:

Question 10

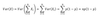
Binomialverteilung Standardabweichung

Answer 10