Konkrete Wahrscheinlichkeitsverteilungen Normalverteilung

Question 1

Definition Normalverteilung

Answer 1

Question 2

Graphische Darstellung d. Wahrscheinlichkeitsdichtefunktion v. ZV mit Normalverteilung: Bedeutung der Parameterwerte

Answer 2

• Parameter µ: bestimmt, bei welchem x-Wert sich das Maximum der Dichtefunktion befindet
• Parameter σ²: legt die “Breite” der Dichtefunktion fest

Question 3

Wichtige Eigenschaften der Normalverteilung

Answer 3

1. Ihre Wahrscheinlichkeitddichtefunktion f(x) hat ihr Maximum an der Stelle x=µ.
2. f(x) ist symmetrisch um µ, d.h.: f(µ+c)=f(µ-c) für alle c∈ℝ. Hieraus folgt u.a.:

• P(X ≤ µ+c)=P(X ≥ µ-c)
• P(X ≤ µ)=P(X ≥ µ)=0.5
  3. f(x) hat eine Glockenform. Je weiter x von µ entfernt, desto kleiner ist die Dichte f(x).

Question 4

Verteilunfsfunktion einer normalverteilten ZV

Answer 4

Erinnerung: Verteilungsfunktionen bei stetigen ZV X

Verteilungsfunktion einer normalverteilten ZV X somit:

Question 5

Beispiele graphische Darstellung d. Dichtefunktion u. Verteilungsfunktion normalverteilter ZV X mit unterschidl. Parameterwerten

Answer 5

Question 6

Erwartungswert einer normalverteilten ZV

Answer 6

Kann aus der allg. Formel für den Erwartungswert für stetige ZV berechnet werden (sehr aufwendig):

Question 7

Varianz einer normalverteilten ZV

Answer 7

Kann aus der allgemeinen Formel für die Varianz füt stetige ZV berechnet werden (sehr aufwendig):

Question 8

Standardabweichung einer normalverteilten ZV

Answer 8

Question 9

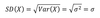
Def. Standardnormalverteilung

Answer 9

Die Normalverteilung mit den Parameterwerten µ=0 und σ²=1

→ Der Erwartungswert einer standardnormalverteilten ZV X ist also E(X)=µ=0, und die Varianz Var(X)=σ²=1

Wahrscheinlichkeitsdichtefunktion der Standardnormalverteilung:

Question 10

z-Standardisierung von normalverteilten ZV

Answer 10

→dies bedeutet, dass jede normalverteilte ZV X in durch z-Standardisierung un eine standardnormalverteilte ZV Z überführt werden kann!