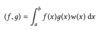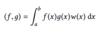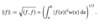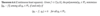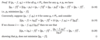Least-sqaures approximation

Question 1

What is the main question in this chapter?

Answer 1

How do we find approximate solutions to overdetermined systems?

Question 2

What is an overdetermined system?

Answer 2

If A is an m x n rectangular matrix with m > n, then the linear system a Ax = b is overdetermined and will usually have no solutions.

Question 3

Define the inner product.

Answer 3

Question 4

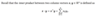
What norm is the inner product related to? And why?

Answer 4

Question 5

What is the angle θ between x and y given by?

Answer 5

Question 6

Define orthogonal.

Answer 6

Question 7

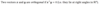
When is the set S = {x₁, x₂, …. , x_n} orthogonal?

Answer 7

Question 8

What is the theorem about an orthogonal set being a basis?

Answer 8

Question 9

Prove the following theorem.

Answer 9

Question 10

Define an orthonormal set.

Answer 10

Question 11

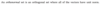
Given an orthogonal set S, how can you construct an orthonomal set S’?

Answer 11

Question 12

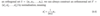
What is the theorem about the columns of a matrix Q being an orthonormal set?

Answer 12

Question 13

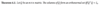
Prove the following theorem.

Answer 13

Question 14

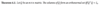
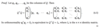
Inner products are preserved under multiplication of what?

Answer 14

Orthogonal matrices

Question 15

Show that inner products are preserved under multiplication by orthogonal matrices.

Answer 15

Question 16

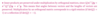
What is the discrete least squares problem?

Answer 16

Find x that minimizes the l₂ norm of the residual ||Ax - b||₂

Question 17

What is the range(A)?

Answer 17

The set of all possible bectors Ax ∈ ℝ^m, where x ∈ ℝⁿ.

Question 18

Why is the range(A) only a subspace of ℝ^m?

Answer 18

Because Ax is a linear combination of columns of A and there are only n < m of them, and in particular it will not, in general, contain b.

Question 19

In discrete least squares what are we looking to minimise?

Answer 19

Question 20

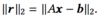
How do you minimise ||r||₂?

Answer 20

By choosing r orthogonal to Ax

Question 21

When minimising ||r||₂ what equation is satisfied?

Answer 21

Question 22

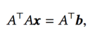
What is the following equation called?

Answer 22

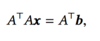
The normal equation

Question 23

Prove the following equation is satisfied when minimsing ||r||₂.

Answer 23

Question 24

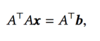
What is the theorem about if a matrix A^TA is invertible?

Answer 24

Question 25

Prove the following theorem.

Answer 25

Question 26

What is the QR decomposition theorem?

Answer 26

Question 27

What is the fastest way to compute Q and R?

Answer 27

Gram-Schmidt orthogonalization.

Question 28

What is the algorithm for Gram-Schmidt

Answer 28

Question 29

How can you construct QR decomposition of A?

Answer 29

Apply Gram-Schmidt to the set of columns of A, this produces a set of orthogonal vectors q_i. Then you write A in the following form.

Question 30

How does QR decomposition help in least squares?

Answer 30

Question 31

What is the continuous least squares problem?

Answer 31

It is to find a polynomial p_n ∈ P_N that minimises ||p_n - f||, in a given inner product.

Question 32

Define an inner product.

Answer 32

Question 33

What does w(x) stand for in the following?

Answer 33

The weight function

Question 34

What is the purpose of the weight function?

Answer 34

To assign varying degrees of importance to errors on different portions of the interval

Question 35

Define the norm ||f|| using the following inner product.

Answer 35

Question 36

What is the continuous least squares theorem?

Answer 36

Question 37

Prove the following theorem.

Answer 37

Question 38

Define a family of orthogonal polynomials.

Answer 38

Question 39

What are the three options for normalising a family or orthogonal polynomials?

Answer 39

Question 40

What is the three-term recurrence theorem?

Answer 40

Question 41

Prove the following theorem.

Answer 41