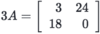Matrices Flashcards
# define: matrix
A
- *rectangular arrangement** of
- *numbers** into
- *rows and columns**.
In plainspeak,
what is a
matrix?
A
compact representation of numbers.
What are the
dimensions
of matrix B?
3 x 2
Pronounced “three by two.”
Rows x Columns
- *Envision** a
- *2 x 3 matrix**.
Rows x Columns
What is
- *another word** for a
- *matrix entry**?
Matrix element
How could you
- *identify** the
- *entry −7** in
- *matrix G**?
g1,3
It’s the entry in the first row and the third column.
What is
element g2,1?
18
It’s in the second row and the first column.
# _define_: augmented matrix
A matrix that
- *represents** a
- *system of equations**.
In an
augmented matrix,
what does each
row represent?
One equation
in the system of equations
In an
augmented matrix,
what does each
column represent?
A
variable
or the
constant terms
in the system of equations
- *Envision** the
- *augmented matrix** that
- *represents** the
- *system below**.
- *Envision** the
- *augmented matrix** that
- *represents** the
- *system below**.
- *Envision** the
- *augmented matrix** that
- *represents** the
- *system below**.
What are the
- *three** elementary
- *matrix row operations**?
Switch any two rows
Add one row to another
Multiply a row by a
nonzero constant
Why can you
switch any two rows in an
augmented matrix?
The
- *order** of the equations
- *doesn’t matter**.
Why can you
add one row to another in an
augmented matrix?
Because you can
- *add two equal quantities** to
- *both sides** of an equation.
Why can you
multiply a row by a nonzero constant in an
augmented matrix?
Because you can
- *multiply both sides** of an equation by the
- *same nonzero constant**.
How do you
- *notate**
- *interchanging rows 1 and 2**?
How do you
- *notate**
- *multiplying row 2 by three**?
How do you
- *notate**
- *replacing row 2** with the
- *sum of rows 1 and 2**?
Just add the corresponding entries.
Just subtract the corresponding entries.
Undefined
Cannot add or subtract matrices with different dimensions.
When working with
matrices,
how do you
refer to
real numbers?
Scalars
Any real number that is
not a part of the matrix is a
scalar.
# _define_: matrix equation
An
- *equation** in which the
- *variable** stands for a
- *matrix**.
# _define_: zero matrix
A
- *matrix** in which
- *all entries are 0**.
When working with
matrices,
what does
O mean?
A zero matrix
What are the
dimensions of the
zero matrix in the equation
B + O = B
given that:
2 x 3
If the dimensions of a zero matrix aren’t given, it’s understood that the dimensions match the dimensions of matrix B.
How would you
notate a
zero matrix with
two rows and four columns?
O2x4
A zero matrix is indicated by O,
and a subscript can be added to indicate the dimensions of the matrix if necessary.
Given
matrices A and O,
A − O = _____?
A
When we add the
m x n zero matrix to
any m x n matrix A, we get
matrix A back.
Given
matrix A,
A + −A = _____?
O
What is the
commutative property of addition?
(applied to matrices)
A + B = B + A
You can
add two matrices in any order and
get the
same result.
What is the
associative property of addition?
(applied to matrices)
(A + B) + C = A + (B + C)
You can
change the grouping in matrix addition and get the
same result.
For example, you can add matrix A to B first, and then add matrix C or you can add matrix B to C and then add this result to A.
What is the
additive identity property?
(applied to matrices)
A + O = A
The
sum of
any matrix A and the
appropriate zero matrix is the
matrix A.
What is the
additive inverse property?
(applied to matrices)
A + (−A) = O
The sum of a
real number and its opposite is
always 0, and so the
sum of any matrix and its opposite gives a
zero matrix.
What is the
closure property of addition?
(applied to matrices)
- A* + B is a matrix of the
- *same dimensions** as
- A* and B.
Due to what
property,
applied to the matrices below,
do we know that
A + B = B + A?
The
commutative property of addition
You can
add two matrices in any order and
get the
same result.
Due to what
property,
applied to the matrices below,
do we know that
(A + B) + C = A + (B + C)?
The
associative property of addition
You can
change the grouping in matrix addition and get the
same result.
Due to what
property,
applied to the matrices below,
do we know that
A + O = A?
The
additive identity property
The
sum of
any matrix A and the
appropriate zero matrix is the
matrix A.
Due to what
property,
applied to the matrices below,
do we know that
A + (−A) = O?
What is the
additive inverse property?
The sum of a
real number and its opposite is
always 0, and so the
sum of any matrix and its opposite gives a
zero matrix.
Due to what
property,
applied to the matrices below,
do we know that
- A* + B is a matrix of the
- *same dimensions** as
- A* and B.
The
closure property of addition
What is the
associative property of multiplication?
(applied to matrices and scalars)
(cd)A = c(dA)
If a matrix is multiplied by
two scalars, you can
multiply the scalars together first,
and then
multiply by the matrix
OR
you can multiply the matrix by one scalar,
and then
the resulting matrix by the other.
What are the
distributive properties?
(applied to matrices and scalars)
c(A + B) = c**A + c**B
and
(c + d)A = cA + dA
A
scalar can be
distributed over
matrix addition.
What is the
multiplicative identity property?
(applied to matrices and scalars)
1A = A
Because 1 • a = a for any real number a, the scalar 1 will always be the multiplicative identity in scalar multiplication.
What are the
multiplicative properties of zero?
(applied to matrices and scalars)
0 • A = 0
and
c • O = O
- In scalar multiplication, 0 times any m x n matrix A is the m x n zero matrix.*
- This is derived from the multiplicative properties of zero in the real number system.*
What is the
closure property of multiplication?
(applied to matrices and scalars)
- cA* is a matrix of the
- *same dimensions** as
- A*.
Due to what
property,
applied to the matrices and scalars below,
do we know that
(cd)A = c(dA)?
The
associative property of multiplication
If a matrix is multiplied by
two scalars, you can
multiply the scalars together first,
and then
multiply by the matrix
OR
you can multiply the matrix by one scalar,
and then
the resulting matrix by the other.
Due to what
property,
applied to the matrices and scalars below,
do we know that
c(A + B) = c**A + c**B
and
(c + d)A = cA + dA?
The
distributive properties
A
scalar can be
distributed over
matrix addition.
Due to what
property,
applied to the matrices and scalars below,
do we know that
1A = A?
The
multiplicative identity property
Because 1 • a = a for any real number a, the scalar 1 will always be the multiplicative identity in scalar multiplication.
Due to what
property,
applied to the matrices and scalars below,
do we know that
0 • A = O
and
c • O = O
The
multiplicative properties of zero
- In scalar multiplication, 0 times any m x n matrix A is the m x n zero matrix.*
- This is derived from the multiplicative properties of zero in the real number system.*
Due to what
property,
applied to the matrices and scalars below,
do we know that
- cA* is a matrix of the
- *same dimensions** as
- A*?
The
closure property of multiplication
# _define_: scalar multiplication
(applied to matrices)
The
- *product** of a
- *real number** and a
- *matrix**
Each entry in the matrix is
multiplied by the given
scalar.
# _define_: *n*-tuple
An
- *ordered list** of
- n* numbers
# _define_: dot product
A
- *single number** obtained from
- *two n-tuples** by
- *summing the products** of the
- *respective entries**
Also called
scalar product
How do you
- *notate** an
- n*-tuple using a
- *variable**?
By a
- *variable** with an
- *arrow on top**
The
product of
two n-tuples of
equal length is
always a
single real number
Take the
- *dot product** of the respective
- *rows of matrix A** and the
- *columns of matrix B**
Specifically, the entry
ci,j is the
dot product of
<strong>→</strong> <strong>→</strong>
ai & bj
For example . . .
Generally,
how do you know whether
matrix multiplication is
defined?
The
number of columns in the first matrix
must be equal to the
number of rows in the second matrix
Generally,
how do you know the
dimensions of the product of
matrix multiplication?
It will have
first matrix’s number of rows
and the
second matrix’s number of columns
(m x n) (n x k):
product is m x k
Is this operation
defined?
If so,
what are the
dimensions of the
product?
Yes,
it’s defined
3 x 2
are the dimensions of the product
Is this operation
defined?
If so,
what are the
dimensions of the
product?
No,
it’s undefined
The would-be factors are
3 x 4 and 3 x 2,
and because the
inside dimensions aren’t the same,
multiplication is undefined.
# _define_: identity matrix
A
- *square matrix** with
- *1’s along the diagonal** from the
- *upper left to bottom right** and
- *0’s everywhere else**
Envision
the matrix
I4.
The n x n identity matrix, denoted
In,
is a matrix with n rows and n columns.
The
product of
any square matrix and the
appropriate identity matrix is always the
original matrix,
regardless of the order in which the
multiplication was performed
The
product of
any square matrix and the
appropriate identity matrix is always the
original matrix,
regardless of the order in which the
multiplication was performed
Applied to the matrices below,
which of the following
is not true?
# _define_: transformation
The
same thing as a
function
(something which
takes in a number and
outputs a number)
BUT while
functions are typically visualized with graphs,
“transformations” are typically visualized as some object moving, stretching, squashing, etc.
How do you represent a
two-dimensional linear transform
with a
matrix?
These are the respective
x- and y-coordinates where the points
(1, 0) and (0, 1)
end up
Note the relationship with I2
How do
- *two dimensional linear transformations**
- *relate** to
- *I2**?
These
- *transformation matrices** are
- *scaled** forms of
- *I2**
Given a
two-dimensional linear transformation,
how do you
determine where a
given vector
ended up?
(x, y) = the vector before transform
(a, c) = where (1, 0) ended
(b, d) = where (0, 1) ended)
Given
matrix A,
what does
| A | mean?
The
determinant of matrix A
Given
matrix A2x2,
how do you
calculate the
determinant of A?
What is the
- *adjugate** of
- *matrix A** below?
Values in the
- descending diagonal are swapped
- ascending diagonal are made opposite
Given
matrix A,
___ • A = I
A−1 • A = I
Also . . .
A • A−1 = I
(Pronounced
“the inverse of matrix A”)
Given
matrix A,
how do you determine
A−1?
A−1 = 1 • adj(A)
| A |
One over the determinant of A
times the
adjugate of A
How do you
know whether a
matrix is
invertible?
A
matrix is invertible
unless the
determinant equals zero
This would require you to divide by zero when determining the inverse, which is an undefined operation
Is
matrix A
invertible?
No
A matrix is invertible
unless its
determinant equals zero
Here . . .
A | = 2•6 − 4•3 = 0
Is
matrix A
invertible?
Yes
A matrix is invertible
unless its
determinant equals zero
Here . . .
A | = 2•6 − 5•3 = −3
What are the
- *steps** to
- *solving a linear system** with
- *matrix equations**?
i.e.
2s – 5t = 7
–2s + 4 = –6
- Represent the system as a matrix
- Multiply each side by the inverse of the matrix, which isolates the variables
- Simplify
