Moments Flashcards
what is centre of mass (or gravity)
the position where the weight of an object appears to act from
it always wants to be in the lowest possible position
talk about humans and centre of mass
humans have to do work to raise the centre of mass
e.g. sit up straight and not slouch
what is the equation for moments?
moments (Nm) = force (N) x perpendicular distance from the pivot to the force (m)
M = Fd
what happened when Cici (more mass) and Tess (less mass) stand on different ends of a balance?
Why?
the balance tipped so that Cici went down to the ground and Tess was raised
Cici and Tess are the same distance away from the pivot but Cici has a greater force han Tess and a thus a greater moment to Tess
the plank is unbalanced
CIci’s moment is anti-clockwise and Tess’ clockwise from the pivot thus the plank rotates anti-clockwise
Explain why the see-saw became balanced with Tess and Nikita in this position relative to Cici
the sum of Tess and Nikita’s force is greater than Cici’s but their distance from the pivot is smaller thus their moments are equal
Cici’s moment is 1200Nm anti-clockwise and Tess’ and Nikita’s is clockwise from the pivot
what is the principle of moments?
the sum of the clockwise moments is equal to the sum of the anti-clockwise moments when the system is in equilibrium
moments are caused by …, but they are not … themselves
they cause objects to turn or …
like forces, they are … quantities and have a direction; these are usually restricted to … or …
moments are caused by forces, but they are not forces themselves
they cause objects to turn or rotate
like forces, they are vector quantities and have a direction; these are usually restricted to clockwise or anti-clockwise
what are moments measured in?
Nm
a door handle is 0.75m from the hinge
the door is closed and a person pulls on the handle with a force of 20N
calculate the moment produced by the person
M = f x d
= 20 x 0.75
= 15Nm
a bus driver uses his right hand to turn his steering wheel
the diameter of the wheel is 40cm and she pulls down on the wheel with a force of 15N
calculate the moment
M = f x d
= 15 x 40
= 300Nm
which direction will the wheel turn?
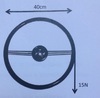
clockwise
describe two ways she could increase the moment on the wheel
pull down with a greater force (force)
make the wheel bigger (distance)
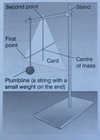
how do you find the centre of mass of an object?
suspend it from two different points (see figure)
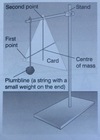
what is the method for finding the centre of mass of a piece of flat card?
suspend the flat card from a pin and let it swing freely
when you do this, the centre of mass of the card is directly below the pin
you can use a ‘plumbline’ to draw a veritcal line on the card from the pin downwards
now repeat this procedure with the card suspended from a different point to give another line
the centre of mass of the card is where the two lines cross
What are A and B?
pivots
A unifrom bridge has a weight of 20,000N. Two supports are placed near the ends, 7.5m from the centre of mass of the bridge. State the value of the support forces at A and B
A = 10,000 N
B = 10,000 N
A car with a weight of 10,000N now parks at the centre of the bridge. State the extra force exerted at A and B
Extra force at A = 5,000 N
Extra force at B = 5,000 N
A similar car drives from A to B at a constant speed. Describe the changes in the support forces acting on A and B, stating values of significant positions of the car along the bridge. You can state the total forces (which include the weight of the bridge), or extra forces (ignoring the weight of the bridge)
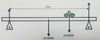
as the car moves away from A, the force acting on A decreases as the force acting on B increases in a directly proportional way in order for the bridge to stay in equilibrium
when the car has moves 1/4 of the way across the bridge the force at A would be 7500N and at B it would be 2500N (exluding the weight of the bridge)
Fa + Fb = the weight of the car when ignoring the weight of the bridge
how do you calculate the mass of ruler?
Wm x d1 = Wr x d2
Explain why Fb increases as the car approaches it
the bridge is in equilibrium
the anti-clockwise and clock-wise moments are equal
Fa + Fb = weight of the car as the resultant force is zero (the bridge is stationary)
the car moving away from A increases the distance from A to car and therefore the anti-clockwise moment about A increases
the car moving closer to B decreases the distance from B to the car but increases the force about B and therefore the clockwise moment increases
Calulate the force of F
M = f x d
10 x 2
= 20 Nm
M = f x d
20 = F x 4
F = 5N
Calculate the distance of d
M= f x d
= 18 x 30
=540 Nm
M= f x d
540 = 36 x d
d = 15
Calculate the force of F (assume cm is m instead)
M = f x d
= 100 x 40
= 4000 Nm
M = f x d
= 40 x 20
= 800 Nm
4000 - 800 = 3200
3200 = 50 x F
F = 64 N
Explain why the ruler is equilibrium. Remember to refer to moments.
“A student investigated equilibrium by using the equiptment in the diagram. The 2N wieght is 60cm from the pivot and the Newton meter is 10.5cm from the pivot.”
the sum of the clockwise moments is equal to the sum of the anti-clockwise moments
(principle of moments)
Show that the upward force is about 10N
“A student investigated equilibrium by using the equiptment in the diagram. The 2N wieght is 60cm from the pivot and the Newton meter is 10.5cm from the pivot.”
M - f x d
2 x 60 = 120 Nm
f = M ÷ d
= 120 ÷ 10.5
= 11.4 N ≈ 10N
The student moves the 2N wieght further away from the pivot while the Newton meter remains in the same position. What happens to F, the value on the Newton meter?
“A student investigated equilibrium by using the equiptment in the diagram. The 2N wieght is 60cm from the pivot and the Newton meter is 10.5cm from the pivot.”
F (the value on the Newton meter) must increase for the ruler to stay in equilibrium
this increase in force is needed to oppose the increase in the clockwise moment which was increased by the increase distance from the pivot
Explain why F increases as the student moves the 2N weight further away from the pivot while the Newton meter remains in the same position
Refer to variables thar are changing and variables that do not change when the 2N weight is moved
“A student investigated equilibrium by using the equiptment in the diagram. The 2N wieght is 60cm from the pivot and the Newton meter is 10.5cm from the pivot.”
When the 2N weight move away from the pivot, the perpendicular distance increased thus increasing the clockwise moment
in order for the ryler to stay in equilibrium, the clockwise moment must be equal to that of the anti-clockwise moment
this means, in order to keep the ruler in equilibrium, the anti-clockwise moment must increase
to increase a moment you must increase either the distance or the force
as the Newton meter (the distance) remains in the same position, the force of the anti-clockwise moment must increase to counter-act and balance out the increased clock-wise moment
A 900N car is parked on a uniform bridge as shown in the diagram. The bridge wieghs 11,000N and is 30m between A and B. The car is 10m from A.
Add arrows and suitable lables (like FA) to represent the force at A, the force at B, the weight of the car, the weight of the bridge, the distance to the weight of the bridge and the distance to the weight of the car
state which force will be greater; the upward force at A or the upward of force at B
the upward force at A
As the bridge and the car is in equilibrium the resultant force on the system is equal to zero
Use this information (Nothing to do with moments yet) to write an equation linking the weight of the car, the weight of the bridge FA and FB
FA + FB = weight of the car and the weight of the bridge
what does ∑mc and ∑mac mean?
∑mc = sum of the clockwise moments
∑mac = sum of the anti-clockwise moments
Take moments about A to calculate the upward force at B
∑ma = ∑mac
Fb x 30 = (Wc x 10) + (Wb x 15)
15 Fb = (900 x 10) + (11,000 x 15)
15Fb = 174,000
Fb = 11600N
The man in the diagram is using a device to hold a 200N bucket of water level
Explain in the system is in equilibrium or not
the system is in equilibrium as the water is level
this means there would be no resultant moment or resultant force so the system must be in equilibrium
The man in the diagram is using a device to hold a 200N bucket of water level
John says: “I think the man will have to exert more than 100N to keep the system in equilibrium.”
Evaluate his comment
He uses correct key words: exerts; equilibrium
His calculations are incorect
the anticlockwise moment is 300Nm:
M = f x d
= 200N x 1.5m
thus, if the man exerted more than 100N the system would not be in equilibrium as:
M = f x d
= +100N x 3m
(this equates to more than 300Nm)
the anti-clockwise moment would be greater than the clockwise moment and thus the system would not be in equlibroum
What will happen to the upward force at A and B as the car moves further away from A?
as the car moves further away from the pivot, A, the perpendicular distance from pivot A increases thus increasing the clock-wise moment
in order for the bridge to stay in equilibrium, the clockwise moment must be equal to the anti-clockwise moment
in this way, as the clockwise moment increases, the anti-clockwise moment must either increase the distance from the pivot or the force
as the length of the bridge is fixed, the force at B must increase to make the anti-clockwise moment equal to the clockwise moment and achieveing equilibrium
A moment is a … effect
A moment is a turning effect
What is a moment?
A moment is the turning effect of a force around a fixed point called a pivot
Where does the centre of mass (gravity) hang?
the centre of mass (gravity) hangs directly below the point of suspension
Through what does an object’s weight act?
an object’s weight acts through the centre of mass
What happens if the anti-clockwise moments do not equal the clockwise moments?
if the anti-clockwise moments do not equal the clockwise moments, there will be a resultant moment
the object will turn
