Newton, Units & Translation

Question 1

What SI unit and common variables are associated with length?

Answer 1

Length or distance has SI units of meters (m).

The variables d and x are used for distance, h for height, z for depth, and r for radius.

Question 2

What SI unit and common variables are associated with time?

Answer 2

Time has SI units of seconds (s).

The variable t is used for time, T is used for period and also has SI units of seconds.

Question 3

What SI unit and common variables are associated with area?

Answer 3

Area has SI units of meters²(m²).

The variable A is used for area, S is used for surface area.

Question 4

What SI unit and common variables are associated with volume?

Answer 4

Volume has SI units of meters³(m³).

The variable V is used for volume.

Question 5

What SI unit and common variables are associated with velocity?

Answer 5

Velocity or speed has SI units of meters/second (m/s).

The variable v is used for velocity (a vector), though rarely used, s may be used for speed (magnitude only, scalar).

Question 6

What SI unit and common variables are associated with acceleration?

Answer 6

Acceleration has SI units of meters/second²(m/s²).

The variable a is used for acceleration (a vector).

Question 7

What two characteristics are necessary to define a vector?

Answer 7

Magnitude and direction.

Question 8

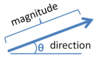
Define:

magnitude of a vector

Answer 8

Magnitude is the quantity, size, or amount and is a scalar value since it lacks direction.

Question 9

Define:

direction of a vector

Answer 9

Direction provides spacial orientation, angle, or path.

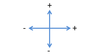
By convention, two perpendicular directions are fixed as positive (right and up) and their opposites as negative (left and down).

Question 10

What is the magnitude of the velocity vector pointing directly down at 5 m/s?

Answer 10

5 m/s.

Magnitude is the quantity, size, or amount.

Question 11

What is the direction of the velocity vector pointing directly up at 13 m/s?

Answer 11

Directly upwards.

Direction is the angle, orientation, or path.

Question 12

Describe the general process for vector addition.

Answer 12

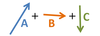
Vectors are added “tip to tail” so that there is a continuous pathway formed from the first arrow through the last one.

The sum vector is made by connecting the original tail to the final tip.

Question 13

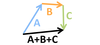
Describe the general process for vector subtraction.

Answer 13

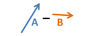
Vectors are subtracted in the same process as addition: “tip to tail”. The direction of the vector being subtracted must be reversed prior to adding.

Question 14

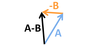
Define:

component vectors

Answer 14

Component vectors represent the magnitude of a given vector along the x axis and y axis.

Generally these are referred to as, for instance, the “x component of [vector]”. In the image below, vector A is shown with its x and y components as A_x and A_y respectively.

Question 15

Give the formula for the x component of a force in the xy plane.

Answer 15

F_x = F * cos θ

In general: [vector]_x = [original vector] * cos θ

Question 16

What is the x component of velocity for a ball thrown upwards at 4 m/s, 30º to the horizon?
(sin(30º) = .5, cos(30º) = .86)

Answer 16

3.4 m/s

v_x = 4*cos (30º)
= 4 (.86)
= 3.4 m/s

Question 17

Give the formula for the y component of a force in the xy plane.

Answer 17

F_y = F * sin θ

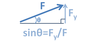
In general: [vector]_y = [original vector] * sin θ

Question 18

What is the y component of velocity for a ball thrown upwards at 4 m/s, 30º to the horizon?
(sin(30º) = .5, cos(30º) = .86)

Answer 18

2 m/s

v_y = 4*sin (30º) = 4 (.5) = 2 m/s

Question 19

Define:

instantaneous velocity (v_o).

Answer 19

Instantaneous velocity is the direction and magnitude of the rate of change of displacement (or position) per unit time.

v_o = Δx / t

or: v_o = p/m

Where p is the object’s momentum and m is its mass.

Question 20

Give the instantaneous velocity for a 3kg block with a momentum of 12kg*m/s.

Answer 20

4m/s

From p = mv, 12 = 3(v), v = 4m/s.

Question 21

Define:

average velocity (v_ave)

Answer 21

Average velocity is the total distance and direction traveled from an initial position, divided by the total time.

v_ave = Δx_total / Δt_total

or: v_ave = (v_f + v_i)/2

Note: the second equation assumes constant acceleration, which is also assumed on the AP exam unless specified otherwise.

Question 22

Give the average velocity for a 1kg block after falling from rest for 2 seconds.

Answer 22

9.8 m/s

From: v = (1/2)at²
v_f= (1/2) (9.8) (2)² = 2 (9.8)
= 19.6 m/s and given: v_i = 0.

From v_ave = (v_f + v_i)/2
v_ave = (19.6 + 0)/2 = 9.8 m/s

Question 23

What formulas can be used to find final velocity, if given initial velocity?

Answer 23

v_f = v_i + at

or: v_f² = v_i² + 2aΔx

Where:
v_f = final velocity in m/s
v_i = initial velocity in m/s
a = acceleration in m/s²
Δx = displacement in m
t = time in s

Question 24

Give the velocity of a 1kg block after falling for 2 seconds from rest.

Answer 24

19.6 m/s

From: v_f = v_i + at
v_f= 0 + (9.8)(2) = 2(9.8)
= 19.6 m/s

Question 25

Define:

acceleration

Answer 25

Acceleration is the rate at which velocity changes per unit of time.

a = Δv / t

Question 26

What must have happened to the value of acceleration, if the same change in distance is now traveled in 1/2 the time?

Answer 26

4x the acceleration.

Since a is proportional to Δx/t², halving t will quadruple a.

Question 27

What is the acceleration always associated with an object in free fall?

Answer 27

9.8 m/s²

This is the acceleration due to gravity, commonly called g. On the AP exam, any falling object is assumed to be in free fall (no air resistance) unless told otherwise.

Note: while it’s convenient to use 10 m/s² for calculations, the AP exam expects you to still choose the correct answer mathematically.

Question 28

How is the maximum height of an object in projectile motion found?

Answer 28

The maximum height of an object in projectile motion can be found by finding the point where the vertical component of velocity, v_y, equals zero. Then input this value into the equation with distance, to solve.

The object moves upwards until it reaches this point, and then starts moving downwards.

Question 29

What is the maximum height of a ball thrown directly upwards from the ground with a velocity of 10 m/s?

Answer 29

The ball’s maximum height is 5m.

The kinematic equation that most easily solves this question is

v_f² = v₀² + 2aΔx

Setting v₀ to 10m/s, v_f to 0m/s, and a to -10m/s² yields:

0 = 100 + 2(-10)Δx
Δx = 5m

Question 30

Define:

air resistance

Answer 30

Air resistance is the frictional force that opposes an object moving in free fall.

F_air = -kv²

The force of air resistance is proportional to the square of the velocity of the object falling. The constant k is a function of the object’s shape and surface area.

Question 31

What is the corresponding change in magnitude of the force of air resistance if an object’s speed doubles?
(assume k remains constant)

Answer 31

Air resistance increases by 4x.

Since F_air is proportional to -v², doubling velocity will quadruple the force. Recall that the negative sign only applies to direction and not magnitude.

Question 32

Define and give units for:

Force

Answer 32

Force is the change in velocity per unit time that a given mass is experiencing. Force can also be thought of as the change in momentum per unit time.

The SI unit of force is the Newton (N),
1N = 1 kg*m/s²

Question 33

What must be done to momentum, for an object to suddenly experience twice as much force on it?

Answer 33

Momentum per unit time must be doubled.

Since force is the change in momentum per unit time, these are directly proportional.

Question 34

Describe Newton’s first law of motion.

Answer 34

aka the Law of Inertia: An object in motion will continue with constant velocity unless acted on by a net force.

Similarly, an object at rest will continue to remain at rest until acted on by a net force.

Question 35

What must be true about the acceleration of an object, if all forces acting on it cancel?

Answer 35

The object has zero acceleration.

Since all forces cancel to be zero, there is not a net force and there will not be a change in velocity. If there is no change in velocity, that is the same as no acceleration.

Question 36

What is the relationship between force, mass, and acceleration in Newton’s second law of motion?

Answer 36

F_net = ma

Note: net force and acceleration are both vectors, and must be pointing in the same direction.

Question 37

What is the proportional change in force to make an object move with twice its original acceleration?

Answer 37

Twice the original force must be applied.

From Newton’s second law, F=ma. Force and acceleration are directly proportional.

Question 38

How does Newton’s third law of motion describe the forces between two objects?

Answer 38

F_1on2 = -F_2on1

For every force from one object on a second, there is an equal and opposite force from the second back on the first.

Question 39

What magnitude of force must exist from apple to an orange in free space, if it’s found that there is a force from the orange to the apple of 5N.

Answer 39

5N

From Newton’s third law, every force excerted must have an equal and opposite force. The negative sign is already factored in, since the question specified direction.

Question 40

What is the formula for gravitational force?

Answer 40

F_g = Gm₁m₂ / r²

Where:
G = gravitational constant in N*m²/kg²
m₁ and m₂ = masses in kg
r = distance between masses in m

Question 41

What is the proportional change in gravitational force between two objects, if the distance between them doubles?

Answer 41

Force is decreased to 1/4.

Since F is proportional to 1/r², doubling r will reduce the force by a factor of 4.

Question 42

What is the proportional change in gravitational force between two objects, if the distance between them halves and each object’s mass also halves?

Answer 42

No change in force.

Since each mass is directly proportional to F, halving each mass will result in 1/4 the original F. But, since F is proportional to 1/r², halving r will result in 4x F. The net change in F is the product both factors: 4(1/4) = 1, no change.

Question 43

What is the more convenient relationship for force on a mass, due to gravity on Earth?

Answer 43

F = mg

Where:
F = force in N
m = mass in kg
g = acceleration due to gravity (9.8 m/s²)

Question 44

What is the magnitude of the force acting downward on an apple with mass .2kg on Earth?

Answer 44

2N.

F = mg = .2(9.8) ≈ 2N

Note: if the apple is resting on the ground, it will also be subject to an equivalent normal force pointing upwards.

Question 45

Define:

Weight

Answer 45

Weight is explicitly the force on an object due to gravity. W=mg

Weight if often confused with mass; an object with one weight on Earth will have a different, lesser, weight on the moon, but its mass will remain constant.

Question 46

What will the proportional weight of an object be on the moon, if the moon has 1/6 Earth’s gravity?

Answer 46

The object will have 1/6 the weight it had on Earth.

Since W is proportional to the acceleration due to gravity, the moon’s lesser gravity will produce a proportionally lesser weight.

Question 47

How could an object’s perceived (or instantaneous) weight seemingly change?

Answer 47

Perceived (or instantaneous) weight is the force pushing back on an object against gravity. This is a specific type of normal force.

A person might experience a decreased instantaneous weight if the ground falls away beneath them, such as if an elevator accelerated downwards.

Question 48

How will a person’s instantaneous weight change if the elevator they are standing in begins to accelerate upwards?

Answer 48

Instantaneous weight while accelerating upwards will be greater than at rest, as the acceleration upwards adds to the normal force that the person experienced while at rest.

If the elevator had accelerated downwards, the person would feel less weight. In fact, if the elevator could accelerate downwards at 9.8m/s² the person would experience weightlessness.

Question 49

Define:

Normal force

Answer 49

When two objects are touching, there exists an opposing force between the two objects and perpendicular to the surface in contact. This is the normal force.

Often, on the AP exam, normal force is opposing the force due to gravity.

Question 50

What is the normal force for a book of mass .5kg sitting stationary on a table?

Answer 50

5N directed towards the book, from the table.

The force pulling down on the book due to gravity is F = mg = (.5)10 = 5N downwards towards the table. Since the book is stationary, we know that normal force is equal and opposite; hence it must also be 5N in magnitude.

Question 51

What is the relationship between normal force and friction for a static object?

Answer 51

Static friction (or rolling friction) is a force that opposes any two surfaces in contact from sliding over each other.

f_s ≤ μ_sF_N

Where:
f_s = force of static friction in N
μ_s = coefficient of static friction
F_N = normal force in N

Question 52

Describe what would happen to a box, if a person pushed directly horizontally on the box with a force of:

• 1/2 μ_sF_N
• μ_sF_N
• 2μ_sF_N

Answer 52

• No motion. 1/2 μ_sF_N will be exerted back by static friction.
• No motion. μ_sF_N will be exerted back by static friction.
• Accelerate forward and begin sliding. 2μ_sF_N is greater than the maximum μ_sF_N force that static friction can resist motion with.

Question 53

What is the relationship between normal force and friction for a sliding object?

Answer 53

Kinetic friction (or sliding friction) is a force that opposes the motion of two surfaces sliding across one another.

f_k = μ_kF_N

Where:
f_k = force of kinetic friction in N
μ_k = coefficient of kinetic friction
F_N = normal force in N

Question 54

Describe what would happen to an already sliding box, if a person continued pushing horizontally on the box with a force of:

• 1/2 μ_kF_N
• μ_kF_N
• 2μ_kF_N

Answer 54

• Eventually come to rest. 1/2 μ_kF_N is less than the force of kinetic friction acting against the box, so friction will slow the box.
• Continue sliding at constant v. μ_kF_N will exactly cancel the force of kinetic friction against the box.
• Accelerate forward. 2μ_kF_N is greater than the force of kinetic friction acting against the box.

Question 55

Why is there an equals sign for the force of kinetic friction, but an inequality for the force of static friction?

Answer 55

Kinetic friction only depends on the composition of the two moving surfaces in contact, hence will be one value.

Static friction opposes any amount of force applied while the object remains immobile, hence its value can vary from zero up to the maximum for those surfaces.

Question 56

In which of the following scenarios is static friction between the surfaces higher than kinetic friction?

• A brick on ice
• A brick on asphalt
• An ice block on glass
• An ice block on rubber

Answer 56

All of them. Static friction is always higher than kinetic friction for any pair of surfaces in contact.

Corollary: it always takes more force to start an object sliding than it does to keep it sliding.

Question 57

What formulas give the component forces for the force due to gravity on an inclined plane?
(note that by covention the “x” axis is along the slope of the plane, and the “y” axis is perpendicular to the plane)

Answer 57

F_x=mg sinθ

F_y=mg cosθ

Since these are opposite from how we normally compute components, a way to remember the x component is: sine is for slope.

Question 58

What calculation will give you the normal force on a box of mass m, on an inclined plane with angle θ?

Answer 58

F_N = -mg cosθ

Since the box is not sinking into the slope, nor launching up off of the slope, the net force acting perpendicular to the slope must be zero. Hence, F_y=-F_N

Question 59

What is the force of static friction, if the box does not start to slide down the plane?

Answer 59

F_s = -mg sin(θ)

There are two forces parallel to the slope of the plane; the component of gravity parallel to the plane, with magnitude mg sin(θ), and the force of static friction, pointing in the opposite direction.

These forces must be equal and opposite to prevent motion.

Question 60

In the pulley system demonstrated below, m₂ is twice the mass of m₁ and there is no net movement. What is the relationship between the tension in the string at points 1 and 2?

Answer 60

The tensions are equal.

A key to all pulley questions is to remember that the tension in the string running through the system is always constant, since it is all one string.

Question 61

What is the force F in the pulley apparatus below, with respect to the mass m₁, assuming that all masses are stationary and no friction exists?

Answer 61

F = m₁g

There are two forces acting on m₁; gravity and tension. If the box isn’t moving, they must be equal and opposite, so T = -m₁g. Since tension is constant through the string, the force on m₂ from tension must also be F = -T = m₁g.

Question 62

What is the force F in the pulley apparatus below, with respect to the mass m₂, assuming that all masses are stationary and no friction exists?

Answer 62

F = -m₂g sinθ

There are two forces acting on the box along the inclined plane: the x component of gravity and the tension in the string. If the box isn’t moving, they must be equal and opposite. Hence F = T = -m₂g sinθ.

Question 63

What is the formula for the centripetal acceleration acting on a body following a circular path with a constant speed v?

Answer 63

a = v²/r

On the AP exam, all circular motion occurs at a constant speed.

Question 64

How does the acceleration experienced by a child on a merry-go-round change if the speed of the merry-go-round doubles?

Answer 64

The velocity increases by a factor of 4.

Since acceleration is proportional to the velocity squared, if the velocity doubles, the acceleration increases by the square of that amount, or 4x.

Question 65

What is the centripetal force F experienced by a body traveling in a circle of radius r at a constant speed v?

Answer 65

F = mv²/r

This comes from F = ma, where a is the centripetal acceleration.

Where:
v = velocity in m/s
a = acceleration in m/s²
m = mass in kg
r = radius of circle in m

Question 66

How does the centripetal force on objects 1 and 2 differ, if both are traveling the same circular path at the same speed, but object 2 is twice as heavy as object 1?

Answer 66

The centripetal force on object 2 (heavier) is twice that on object 1 (lighter).

Centripetal force is F = mv²/r. Since F is proportional to m, with all else equal, the force on the heavier object will be proportionally larger.

Question 67

How does the centripetal force on objects 1 and 2 differ, if both are the same mass and traveling the same circular path, but object 2 is moving three times as quickly as object 1?

Answer 67

The centripetal force on object 2 is nine times that on object 1.

Centripetal force is F = mv²/r. Since F is proportional to v squared, with all else equal, the force on the heavier object will be larger by the square of the velocity difference.

Question 68

Define:

a vector field

Answer 68

A vector field is a function that assigns a vector to every point in space.

The only common fields on the AP exam are force fields, which can be used to interpret the force an object at any given point in space will experience. Common examples are electric fields and gravitational fields.

Question 69

What is the direction of the force experienced by an object placed at point A in the gravitational field depicted below?

Answer 69

The object feels a force down and to the left.

This is the direction the vectors in the vicinity of point A are pointing, and these vectors represet the forces experienced by objects at these locations.

On the AP exam, fields are assumed to be of uniform density until told otherwise.

Question 70

Where is the magnitude of the field depicted below greater, point A or point B?

Answer 70

The magnitude of the field is greater at point B.

The magnitude of a field can be estimated from the density of the field lines in this location. The greater the density, the larger the magnitude of the field. The field lines are packed more tightly at point B than at point A, hence the magnitude of the field is greater there.