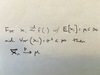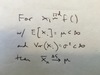Probability Flashcards by Kyle Webb

Definition of sample space

In an experiment, the set of all possible outcomes is the sample space (S)

How well did you know this?

Not at all

Perfectly

Definition of an event and written form

Any outcome in S (E), where E={x in S: x in E}

How well did you know this?

Not at all

Perfectly

7 set operations

Union, intersection, compliment, communicative, associative, distributive, De Morgan’s Law

How well did you know this?

Not at all

Perfectly

Definition of disjoint/ mutually exclusive events

Events A and B are mutually exclusive when their intersection is the empty set

How well did you know this?

Not at all

Perfectly

Definition of pairwise mutually exclusive

For any two subsets of S (A1,A2,A3,…), their intersection is the empty set

How well did you know this?

Not at all

Perfectly

Partition

If A1,A2,A3… are pairwise mutually exclusive and all these sets comprise a set S, then the set {A1,A2,A3,…} partitions S

How well did you know this?

Not at all

Perfectly

Definition of sigma algebra

B, a collection of subsets in S is a sigma algebra if it satisfies the following properties 1) The empty set is contained in B 2) If A is in B then A^c is in B 3) If A1,A2,A3,… are in B then UAi are in B

How well did you know this?

Not at all

Perfectly

What is the largest number of sets in a sigma algebra, B, with n sets?

2^n

How well did you know this?

Not at all

Perfectly

Definition of probability

Given a sample space S with sigma algebra B, a probability function (or measure) is any assigned, real-valued function P with domain B that satisfies the Kolmogorov Axioms.

How well did you know this?

Not at all

Perfectly

Kolmogorov Axioms

1) P(A)>=0, for any A in B 2) P(S)=1 3) For A1,A2,A3,… in B and are pairwise mutually exclusive then P(UAi)=SUM P(Ai)

How well did you know this?

Not at all

Perfectly

1) Gamma Distribution with different parameterizations
2) Expected values and variances of those distributions
3) Gamma funciton
4) Properties of Gamma funciton
5) MGF

How well did you know this?

Not at all

Perfectly

1) Exponential Distribution with different Parameterizations
2) Different expected values and variances
3) MGF

How well did you know this?

Not at all

Perfectly

1) Bernoulli Distribution
2) Expected value and variance
3) MGF

How well did you know this?

Not at all

Perfectly

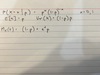
1) Geometric Distribution with different parameterizations
2) Expected values and variances
3) MGF (Also special rule to help solve this)

How well did you know this?

Not at all

Perfectly

1) Poisson Distribution
2) Expected value and variance
3) MGF

How well did you know this?

Not at all

Perfectly

1) Binomial Distribution
2) Expected value and variances
3) MGF

How well did you know this?

Not at all

Perfectly

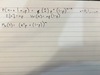
1) Beta Distribution
2) Expected value and variance
3) Beta Funciton
4) Expectation of nth term

How well did you know this?

Not at all

Perfectly

1) Bivariate Normal
2) Conditional expectation
3) Conditional variance

How well did you know this?

Not at all

Perfectly

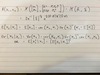
1) Normal and standard normal Distributions
2) Expected values and variances
3) MGFs

How well did you know this?

Not at all

Perfectly

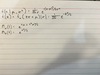
1) Continuous Uniform Distribution
2) Expected value and variance
3) MGF

How well did you know this?

Not at all

Perfectly

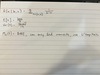
1) Multinomial Distribution
2) Expected value and variance
3) Multinomial Theorem
4) cov(x_i,x_j)

How well did you know this?

Not at all

Perfectly

Bonferonni Inequality

Pr(A∩B)≥Pr(A)+Pr(B)-1

How well did you know this?

Not at all

Perfectly

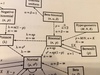
Table of ordered, non-ordered, with replacement, without replacement

How well did you know this?

Not at all

Perfectly

Fundamental Theorem of Counting

For a job which consists of k tasks and tere are n_i ways to accomplish each ith task then the job can be accomplished in (n₁n₂…n_k) ways

How well did you know this?

Not at all

Perfectly

Inequality between unordered with replacement and without replacement

Opposite of this

Binomial Theorem

Paschal's Formula

Three useful properties of binomial coefficients

Bayes' rule (for 2 sets and generally)

Definition of conditional independence

A is conditionally independent of C given B if P[A|B,C]=P[A|B]

Total Law of Probability

Definition of a random variable

A function from a sample space S into the real numbers Formally: P[X=x_i]=P[s_j in S: X(s_j)=x_i]

Conditions for a function to be a CDF (iff)

If RV's have the same cdf then...

X and Y are iid

Can a RV be both discrete and continuous?

Yes

If X and Y are iid (F_X(x)=F_Y(x)) then does this mean X=Y?

A functin f(x) is a pdf (or pmf) iff

Definition of absolutely continuous x

X is absolutely continuous when it is both continuous and differentiable for all x

For a RV x, and Y=g(x), what does f_y(y) equal? (A transformation of random variable)

Let X have cdf F_X(x), let Y=g(X), and let X={x: f_X(x)\>0} and Y={y:y=g(x) for some x in X} What if g is an increasing/ decreasing function on X?

1) If g is an increasing function on X, F_Y(y)=F_X(g^-1(y)) 2) If g is a decreasing function on X and X is a continuous random variable, F_Y(y)=1-F_X(g^-1(y))

Is it always true that E[g(x)]=g(E[x])?

How to find a moment generating function M_X(t) and the moments of a probability distribution

M_X(t)=E[e^tx] dⁿ/dtⁿ M_X(t=0)

Three properties of MGFs

3 mathematical properties

Explain hypergeometric distribution in words

In the presence of two options, the distribution evaluates K selected from M objects from option 1 out of N total objects.

Explain the negative binomial in words

Explains how many trials need to occur to obtain n successes

Memoryless Property

Shapes of Beta distributions

General idea of Poisson process

Two major ways to determine exponential families with respective terms explained

Definition of curved and full exponential family

A curved exponential family is when the number of parameters for an exponential family is less than k A full exponential family is when the number of parameters equals k

Definitions of location, scale, and location-scale families

Location family is one that takes a pdf and includes it in the family of pdfs indexed by the finite parameter u such that f(x-u) remains in the family Scale family is one that takes a pdf and includes it in the family of pdfs indexed by the positive parameter s such that (1/s)f(x/s) remains in the family Location-scale is just a combination of the two

Markov Inequality

Chebyshev's Inequality

How to find E[X₂|X₁] given a joint probability function for the discrete and continuous cases

Given f(X₁, X₂) what is E[X2] (for discrete and continuous case)

If X₁ and X₂are independent and Z=X₁ + X₂then what does this say about the mgf's for these variables?

M_z(t)=M_X1(t)M_X2(t)

What is the equation for bivariate transformations for the continuous case?

If a joint probability function can be factorized what does this say about its factors?

They are independent

Basic idea of Hierarchical models

You are given f(X|Y) and f(Y) and need to find f(X)

E[X] in terms of conditional expectations for hierarchical models

E_Y[E_X[X|Y]]

Var(Y) in terms of conditional expectations for hierarchical models

E_X[Var_Y(Y|X)]+Var_X(E_Y[Y|X])

Two forms of covariance

Correlation equation

cov(aX,bY)=

acov(X,Y)b

cov(X+Y,W+Z)=

cov(X,Z)+cov(X,W)+cov(Y,W)+cov(Y,Z)

Given data, basic difference between Classical and Bayesian approach

Classical model uses simulated or given distribution to obtain some fixed, unknown constant (the parameter) The Bayesian model assumes the parameter is a random variable and relies on prior knowledge of this variable and posterior enhancement through collected data. This method utilizes the idea of exchangability (conditional independence) for the samples

Cauchy-Schwarz Inequality

Holder's Inequality

Jensen's Inequality

If x₁,x₂,x₃,... are mutually independent then what does this say about the function of this vector of mutually independent x's, the product of Expected transformations for each x, and their MGFs?

If _X_₁,_X_₂,_X_₃,... are independent then what does this say about the transformation of these vectors?

What is the "mission" of a statistician?

To learn from data (by obtaining a sample) to make judegements about the unknown (through populations and their parameters)

What is the connection between a sample and a population?

Probability (a measure of randomness/stochasticity)

What is a statistic

A summary of the sample

Equation for S²

Convergence in Probability

WLLN

Convergence in Distribution

Convergence almost surely

SLLN

Definition of consistent

A statistic is consistent when it converges in probability to the truth

Central Limit Theorem

Comparison of convergence almost surely and convergence in probability

CAS is stronger, if CAS holds then CIP holds, but not always the converse

Comparison between convergence in probability and convergence in distribution

CIP is stronger because if CIP holds then CID holds, but not always the converse

Slutsky's Theorem

Three things necessary for proving x follows a t distribution

1. E[X] (X bar) and S² are independent 2. E[X}~N(u,sig²/n) 3. (n-1)/(sig²)S²~X²_n-1

Things to remember: a) If each x_i follows a normal then x²_ifollows what dist? b) SUM( x²_i) follows what distribution (sum to n) c) A chi squared distribution (with p degreees of freedom) follows what distribution with certian parameters? d) SUM(x_i-E[X])=? e) SUM(x_i-u)²=? f) S²=? (not just usual equation)