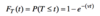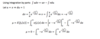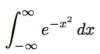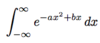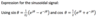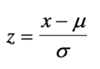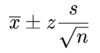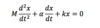Questions

Question 1

Do the first part of the question.

What is the question trying to convey?

Answer 1

By saying r,s = 1,2,3,4

It is saying any combination of the following set of values…

So if you choose 1 and 2.

You multiply the matrix 1 by 2, and then you multiply the matrix 2 by 1.

Question 2

What should you think about doing when your see this type of question?

Answer 2

The angles are already given, so try and simplify the expression as much as possible.

Don’t convert to Euler exponential form immediately.

Question 3

How would you solve this?

Answer 3

If the argument is the same magnitude but a different sign then the value must be on the opposite side of the pi circle, offset by pi.

Question 4

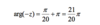
How would this question be solved?

Answer 4

We know that the conjugate has the opposite sign for the complex number part of the cartesian representation.

As such if arg(z) has a positive ratio between b and a, arg(z) for the conjugate must be a negative ratio.

Question 5

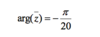
How do you solve this?

How would you start solving the dimensions?

Answer 5

Define all the units that are used.

They should form a product with each other, and each dimension should have a power.

With respect to the variable whose dimension you’re trying to find, define the powers.

Solve each of the power equations obtained. For example, if the variables come out as being dimensionless, all the powers should be equated to zero.

Question 6

What did need to remember about these questions

Answer 6

You confused the x and y in the linear regression equations.

Make sure to choose the right x and y.

Carefully plug the numbers in your calculator, its easy to mess up.

Question 7

Besides solving the questions, what is an important thing to remember about differentiating when there are two variables in a term?

Answer 7

Question 8

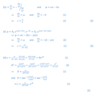
How would this be solved?

Answer 8

Question 9

?

What do you need to remember about question b)

Answer 9

When diff. Bte^-t remember that you need to apply the product rule since you’re multiplying two varaibles.

Question 10

Solve C)

Answer 10

Question 11

Solve d)

Answer 11

Question 12

What is something you need to remember when doing question with trig?

Answer 12

Leave the trig calc for the end!!

You never know when you can simplify using indentities.

If you solve, you wont be able to identify any of them…

Question 13

Solve c)

Answer 13

Question 14

What is the order and degree of this differential equation?

What do you need to remember?

Answer 14

Question 15

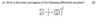
Linear and Non-linear

Answer 15

Question 16

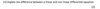
Why do we need to transform non-linear equations.

Answer 16

• Solutions to linear equations can be expressed in terms of a general solution, which is not usually the case for non-linear equations.
• Linear solutions have explicitly defined solutions while non-linear equations do not. Also, non-linear equations may or may not have implicitly defined solutions.

Question 17

In other words, find the expectation.

Answer 17

Question 18

Obtain an expression for the probability that the manufacturing plant will fail within a time 𝑡₀ of continuous operation.

Answer 18

Question 19

Calculate d) given that the expected value(mean time to failure) was found to be 1/Vc

What did you learn from this question?

Answer 19

• That E(X²) applied to function turns out to be equal to E[x²f(x)].
• That you can factor out a variable from a integral, to convert it to an integral you know the value of. Bear in mind if you are factoring out a variable, it can’t be the variable you’re integrating against.

Question 20

Solve e) given that the probability the plant is going to fail within time t ₀ was calculate to be 1−𝑒^v_c*t₀ .

Answer 20

Question 21

What can you do to the negative sign of the magnitude in polar form?

Answer 21

You can move it to the angle…

Question 22

What is something you constantly need to be thinking about when doing the exam?

What would be a good habit to employ in and outside of the exam?

Answer 22

Never forget/drop negatives…

Habit:

Draw negatives really clearly/thickly.

Use a thicker pen or a different color so it stands out.

Question 23

When asked to find a confidence interval for a normal distribution and the z-values do not exactly add up, do you take the lower or higher value?

Using the normal distribution table what is the answer for 6)?

Answer 23

You take the lower value…

Question 24

What do they mean when they say “The proportion of all manufactured items of a certain kind that are defective is 0.04 . Use this to estimate the probabilities that in a batch of 100 of these items”

Answer 24

That out of manufactured items the probability of defect was 0.04.

By multiplying 100 by 0.04 you’ll get the expected mean value of defects for the sample.

Question 25

When you need to calculate the probability that something is going to occur in the future (poisson), what equation do you use?

Answer 25

Question 26

Answer 26

Question 27

How would you go about solving this type of question?

Answer 27

In the hints, they indicate that you need to maximize the compound probability. You can do that by minimising the function in the sum.

To find minimum find derivative wrt a.

From observation, we can see that the sum of xt divided by n is equal to the mean of the product of the two variables multiplied.

Similarly for t² .

The current equation does not exactly match, so divide by 2 and n. Transpose mean of xt and t² into the equation.

Question 28

When doing linear regression equations, what is good practice?

Answer 28

write down the individual values of all the sums you calculate, you might have to use them to calculate another parameter.

Question 29

?

What do you have to remember about this question

Answer 29

That you cannot split a derivative term such as dt across two terms.

If it is split, arrange the expression in such a way that both sides have one term.

Question 30

How do you find the probability distribution function if isn’t given in the formula booklet?

Answer 30

Using the equations under the cumulative distribution function section.

It is important to classify the data you’re looking at properly. Is it continuous or discrete?

Question 31

When calculating the mean/expectation of a function what do you most likely need to do ?

Example attached.

Answer 31

Using integration by parts.

Question 32

When you’re calculating the expectation (or any other integral) across a range and need to use integration by parts, what do you need to make sure you calculate?

Answer 32

Make sure you apply the definite range across both terms obtained from the integration by parts.

Question 33

When you have to integrate a function like the one attached, what should come to mind?

Answer 33

Using the Gaussian integrals

The one you need to use is attached below.

Question 34

What is the equation for the 95% confidence interval?

Answer 34

Question 35

What is the Gaussian integral of this function?

Answer 35

Question 36

What is the gaussian integral of this function

Answer 36

Question 37

How do you solve this ?

Answer 37

Question 38

solve c)

Answer 38

Question 39

If you get this sort of sinusoidal signal, how should you represent it ?

Answer 39

Using complex numbers.

Question 40

Solve!

Answer 40

Question 41

When they ask you what the least squares fit is, what do you do?

Answer 41

Use least squares regression to determine the equation.

Question 42

How do you calculate the z score ?

Answer 42

where x is a data point

mu the mean

and sigma the std deviation

Question 43

When do you use this equation for confidence interval calculation?

Answer 43

When you do NOT know the POPULATION mean.

However, you do have a sample mean.

Question 44

What is the category of this differential equation?

Answer 44

This is a second order, homogeneous, linear ordinary differential equation.

Question 45

Suppose, the historical record shows that annual rainfall in a certain catch basin follows N(60, 15) (inches)

What is the probability that in a future year the annual rainfall exceeds 70 (inches)?

Answer 45

remember that the phi(2/3) is referring 1/sqr(2pi) * exp(-0.5z²)

Question 46

If you have got the following normal distributions what would be the combination of the normal variables?

Given that they are mutually independent.

Answer 46

Note how the standard deviations have been squared and have an overarching square root.