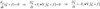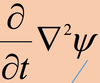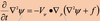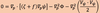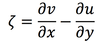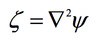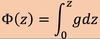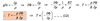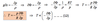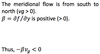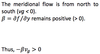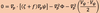Chapter 1: Analysis of Mid-lat syn systems using balance equations Flashcards
the two derived scalar quantities of the horizontal wind
Stream function
velocity potential
stream function is represented by
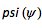
velocity potential is represented by
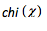
The horizontal wind is then represented by these scalars as:
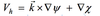
the term means
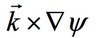
the term means
psi represents
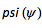
Stream function
chi represents
velocity potential
the following equation is the
The horizontal wind
the rotational (non-divergent) part of horizontal wind is represented by the term
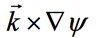
the divergent (irrational) part of horizontal wind is represented by the term
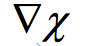
Stream function, velocity potential are the
two derived scalar quantities of the horizontal wind
The scalar equations for u and v can then be written in form of (stream function) and (velocity potential)as
If one of the scalars (stream function) or (velocity potential) is set equal to zero, then the wind that remains can be one of the following
Non-divergent or Rotational wind:
in non-divergent:
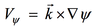
Non-divergent or Rotational wind:
in scalar notation:
irrotational or divergent wind:
the irrotational wind:
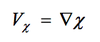
irrotational or divergent wind:
in scalar notation:
the following stands for
vorticity
vorticity in terms of stream function
For horizontal motion that is rotational (non-divergent), the velocity components are given by
Vorticity (ع ) in terms of streamfunction
substituting u and v for ع
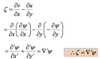
the velocity field and the vorticity can both be represented in terms of
the variation of the single scalar field, (psi)
…………………………… and ……………………… can both be represented in terms of the variation of the single scalar field, (psi)
the velocity field
the vorticity
Obtain an expression for divergence of an irrotational wind
The barotropic vorticity is written as
the barotropic vorticity states that
the absolute vorticity is conserved following the hor. motion.
The barotropic vorticity equation can be written as
prognostic eqn. for vorticity
The barotropic vorticity equation can be written as a prognostic eqn. for vorticity in the form:
the following term represents
local tendency of relative vorticity
the following term represents
advection of absolute vorticity
prognostic equation for vorticity’s condition
prognostic equation for vorticity can be solved
numerically
prognostic equation for vorticity can be solved numerically to
predict the evolution of the streamfunction
prognostic equation for vorticity can be solved numerically to predict the evolution of the stream function, and hence
of the vorticity and wind fields.
The QG vorticity equation in pressure coordinates can be written as
the following equation is a
prognostic equation for the geostrophic relative vorticity.
The QG vorticity equation in pressure coordinates states that
the local change of geostrophic relative vorticity is a function of three terms
The QG vorticity equation in pressure coordinates states that the local change of geostrophic relative vorticity is a function of three terms
- A) the geostrophic horizontal advection of geostrophic relative vorticity,
- (B) the geostrophic meridional advection of planetary vorticity, and
- (C) the vertical stretching of planetary vorticity .
terms A and B in the QG vorticity equation related to
horizontal advection of geostrophic relative vorticity and meridional advection of planetary vorticity.
A
B
C
D
E
F
G
H
I
the following is shown by the …………………………….
500 hPa geopotential field
_East of the trough (Region-II):_
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the ……………. of the ………………..
base of the trough
East of the trough (Region-II):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the base of the trough where the ………… is ………………………….
vorticity is cyclonic عg >0
East of the trough (Region-II):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the base of the trough where the vorticity is cyclonic to region of
anti cyclonic vorticity (عg < 0)
East of the trough (Region-II):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the base of the rough where the vorticity is cycloncic to region of anticyclonic vorticity.
this implies ………………………………………
thus
an increase in geostrophic relative vorticity (PVA).
East of the trough (region -II)
meridional Adv of planetary vorticity
the meridional flow is from ……………….. ( )
south to north
vg > 0
East of the trough (region -II)
meridional Adv of planetary vorticity
the meridional flow is from south to north (vg>0)
…………………….. is ………………. ( )
East of the trough (region -II)
meridional Adv of planetary vorticity
The meridional flow is from south to north (vg > 0).
= ⁄ is positive (> 0).
thus
West of the trough (Region-I):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the ……………. of the ………………..
Apex of the ridge
West of the trough (Region-I):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the apex of the ridge where …………….. is ………………
the vorticity is anticyclonic (عg < 0)
West of the trough (Region-I):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the apex of the ridge where the vorticity is anticyclonic (عg < 0) to region of …………………….. ( )
cyclonic vorticity (عg >0)
West of the trough (Region-I):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the apex of the ridge where the vorticity is anticyclonic (عg < 0) to region of cyclonic vorticity (عg >0)
this implies ………………. in ………………………….. ( )
a decrease
geostrophic relative vorticity (NVA)
West of the trough (Region-I):
Hor. Adv. Geostrophic Rel. Vorticity:
Large-scale flow is directed from the apex of the ridge where the vorticity is anticyclonic (عg < 0) to region of cyclonic vorticity (عg >0)
this implies a decrease in geostrophic relative vorticity (NVA)
Thus
West of the trough (Region-I):
Meridional Adv. of planetary vorticity
The meridional flow is from ……………… to ………………… ( )
north to south (vg < 0)
West of the trough (Region-I):
Meridional Adv. of planetary vorticity
b= ……………………… is …………………. ( )
thus
Thus, the two advection terms are of …………………….sign in both the regions.
opposite
Which of the two advection terms dominates the other?
For shortwave troughs, or those of
zonal (east-west) extent less than approximately 3,000 km
Which of the two advection terms dominates the other?
For shortwave troughs, or those of zonal (east-west) extent less than approximately 3,000 km, ……………………………..dominates over ………………………………
the geostrophic horizontal advection of geostrophic relative vorticity
the geostrophic meridional advection of planetary vorticity.
Which of the two advection terms dominates the other?
For shortwave troughs, or those of zonal (east-west) extent less than approximately 3,000 km, the geostrophic horizontal advection of geostrophic relative vorticity dominates over the geostrophic meridional advection of planetary vorticity. Thus, these features generally move ……………… with the ………………………..
eastward
westerly large-scale flow
Which of the two advection terms dominates the other?
For longwave troughs, or those of
onal extent greater than approximately 10,000 km
Which of the two advection terms dominates the other?
For longwave troughs, or those of zonal extent greater than approximately 10,000 km, …………………………………………dominates over …………………………………
the geostrophic meridional advection of planetary vorticity
the geostrophic horizontal advection of geostrophic relative vorticity.
Which of the two advection terms dominates the other?
For longwave troughs, or those of zonal extent greater than approximately 10,000 km, the geostrophic meridional advection of planetary vorticity dominates over the geostrophic horizontal advection of geostrophic relative vorticity. Thus, to ………………………..
first approximation
Which of the two advection terms dominates the other?
For longwave troughs, or those of zonal extent greater than approximately 10,000 km, the geostrophic meridional advection of planetary vorticity dominates over the geostrophic horizontal advection of geostrophic relative vorticity. Thus, to first approximation, these features move ……….. or …………………. against the ………………………
westward, or retrogress, against the westerly large-scale flow.
Troughs of ……………………………extent (between …………………..) tend to move……………………….
intermediate zonal
3,000-10,000 km
eastward
Troughs of intermediate zonal extent (between 3,000-10,000 km) tend to move eastward, but at a rate of speed ……………………………… than that of the …………………………………
slower to much slower
westerly large-scale flow.
When there is rising motion:
When there is rising motion:
When there is rising motion:
When there is rising motion:
When there is rising motion:
rising motion gives rise
to an increase in geostrophic relative vorticity
By analogy, sinking motion implies a
decrease in geostrophic relative vorticity.
divergence equation can be obtained as
this equation is called
the balance equation
the balance equation can be used to find
the balance equation. It can be used to find if Φ is known, or Φ if is known.
It is useful for example, if we wish to compute the
forcing functions in the height tendency and quasi-geostrophic w equations , in the absence of height (Φ) data
It is useful for example, if we wish to compute the forcing functions in the height tendency and quasi-geostrophic equations , in the absence of height (Φ) data.
STEPS (step 1)
- The vorticity field can be computed from the wind field, if it is available.
It is useful for example, if we wish to compute the forcing functions in the height tendency and quasi-geostrophic equations , in the absence of height (Φ) data.
STEPS (step 2)
The stream function can then be determined from vorticity using eq.7, given proper boundary conditions.
It is useful for example, if we wish to compute the forcing functions in the height tendency and quasi-geostrophic equations , in the absence of height (Φ) data.
STEPS (step 3)
Then, the geopotential height field Φ can be computed from equation (11), again given proper boundary conditions.
It is useful for example, if we wish to compute the forcing functions in the height tendency and quasi-geostrophic equations , in the absence of height (Φ) data.
STEP 4
Since, temperature is related to the vertical gradient of Φ (explained below) through the hydrostatic equation, we can compute temperature from wind field.
The geopotential Φ at any point in the Earth’s atmosphere is defined as
he work that must be done against the Earth’s gravitational field to raise a mass of 1 kg from sea level to that point.
The geopotential Φ at any point in the Earth’s atmosphere is defined as the work that must be done against the Earth’s gravitational field to raise a mass of 1 kg from sea level to that point.
In other words, Φ is
the gravitational potential energy per unit mass.
In other words, Φ is the gravitational potential energy per unit mass. The units of geopotential are
J kg−1 or m2 s−2
The work (in joules) in raising
1 kg from z to z +dz is gdz
The work (in joules) in rising 1 kg from z to z +dz is gdz. the geopotential Φ(z) at height z is thus given by
The work (in joules) in rising 1 kg from z to z +dz is gdz. the geopotential Φ(z) at height z is thus given by
where the geopotential Φ 0 at sea level (z = 0) has been taken as
zero
the thickness of the layer of air between two isobaric surfaces is proportional to the mean temperature of air in the layer.
the equation states that
the thickness of the layer of air between two isobaric surfaces is proportional to the mean temperature of air in the layer.
……………………………………… is conserved following the hor. motion.
the absolute vorticity
……………………………………………. can be written as a prognostic eqn. for vorticity
The barotropic vorticity equation
………………………………………….. can be solved numerically
prognostic equation for vorticity
………………………………………………………………………………… predict the evolution of the stream function
prognostic equation for vorticity can be solved numerically to
…………………………………………………………………… the local change of geostrophic relative vorticity is a function of three terms (A) the geostrophic horizontal advection of geostrophic relative vorticity, (B) the geostrophic meridional advection of planetary vorticity, and (C) the vertical stretching of planetary vorticity
the QG vorticity equation in pressure coordinates
……………………………………………… related to horizontal advection of geostrophic relative vorticity and meridional advection of planetary vorticity
consider the terms-A and B
east of the trough (region-II)
hor. Adv. Geostrophic Rel. Vorticity
East of the trough (Region-II)
Meridional Adv. of Planetary Vorticity
West of the trough (Region-I)
Hor. Adv. Geostrophic Rel. Vorticity
West of the trough (Region-I)
Meridional Adv. of Planetary Vorticity
the balance equation
……………………………………………………………. the work that must be done against the Earth’s gravitational field to raise a mass of 1 kg from sea level to that point.
The geopotential Φ at any point in the Earth’s atmosphere
J kg−1 or m2 s−2 are the units of
geopotential
