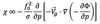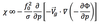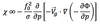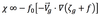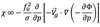chapter 2: Analysis of Mid-latitude Synoptic Scale Systems using QG Height Tendency Equation Flashcards
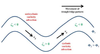
The QG Height Tendency Eq. can be expressed as:
the equation is a
partial differential equation describing the local change of the geopotential height (Φ) on an isobaric surface with respect to time
There are three forcing terms on the right-hand side of The QG Height Tendency Eq. From left to right, these forcing terms represent:
- Geostrophic vorticity advection
- Differential thermal advection and
- Differential diabatic heating.
The QG Height Tendency Eq. is applied to
the study of troughs and ridges in the middle troposphere – often at 500 hPa – and not at the surface
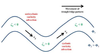
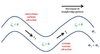
The contribution to the local geopotential height tendency exclusively due to geostrophic vorticity advection can be expressed by:
The contribution to the local geopotential height tendency exclusively due to geostrophic vorticity advection can be expressed by:
It depicts the
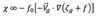
advection by the geostrophic wind of the geostrophic relative (عg) and planetary vorticity (f)
Cyclonic geostrophic vorticity advection will result in
local decrease in geopotential height with time
Cyclonic geostrophic vorticity advection will result in local decrease in geopotential height with time, because:
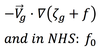
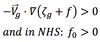
Cyclonic geostrophic vorticity advection will result in local decrease in geopotential height with time, because:
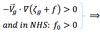
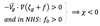
Cyclonic geostrophic vorticity advection will result in local decrease in geopotential height with time, because:
Anticyclonic geostrophic vorticity advection will result in
local increase in geopotential height with time
Anticyclonic geostrophic vorticity advection will result in local increase in geopotential height with time, because:
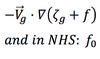
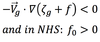
Anticyclonic geostrophic vorticity advection will result in local increase in geopotential height with time, because:
Anticyclonic geostrophic vorticity advection will result in local increase in geopotential height with time, because:
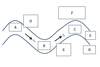
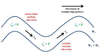
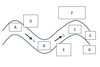
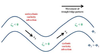
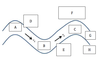
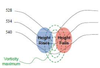
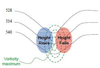
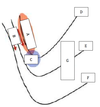
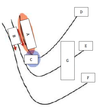
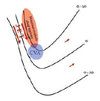
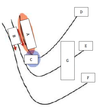
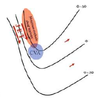
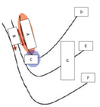
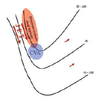
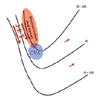
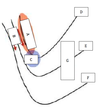
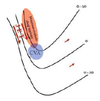
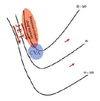
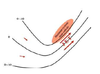
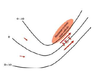
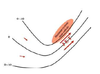
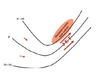
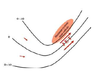
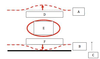
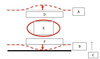
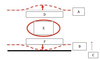
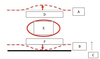
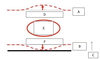
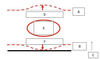
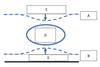
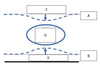
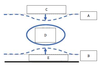
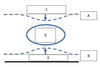
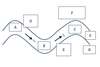
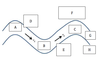
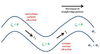
In an idealized trough/ridge scenario where the geostrophic wind is
uniform everywhere
In an idealized trough/ridge scenario where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is ………………………. in the base ……………………………
maximized
of each trough
In an idealized trough/ridge scenario where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is ………………………….. in the apex …………………………..
minimized
of each ridge
In an idealized trough/ridge scenario where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is maximized in the base of each trough
Thus, there is an …………………………… geostrophic vorticity advection to the ……………………………… axis
anticyclonic
west of the trough
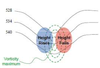
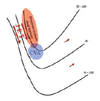
In an idealized trough/ridge scenario where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is (minimized) in the (apex) of each (ridge).
Thus, there is an ……………………. geostrophic vorticity advection to the…………………………….
(cyclonic)
west of the trough axis
n an idealized trough/ridge scenario where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is maximized in the base of each trough
Thus, there is an anticyclonic geostrophic vorticity advection to the west of the trough axis, which is associated with a tendency for height …………
rises
In an idealized trough/ridge scenario (Fig.1), where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is (minimized) in the (apex) of each (ridge).
Thus, there is an (cyclonic) geostrophic vorticity advection to the west of the trough axis, which is associated with a tendency for height ………..
falls
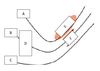
A
B
C
D
E
F
G
H
A
B
C
D
E
F
At the center of a cyclonic vorticity maximum, the height tendency is
zero.
Since the geostrophic wind blows
parallel to contours of constant geopotential height
Since the geostrophic wind blows parallel to contours of constant geopotential height, geostrophic absolute vorticity advection does
not result in the amplification (or intensification) of troughs and ridges.
geostrophic absolute vorticity advection does not result in the amplification (or intensification) of troughs and ridges.
Rather, it results in
their movement from one location to another.
geostrophic absolute vorticity advection does not result in the amplification (or intensification) of troughs and ridges.
Rather, it results in their movement from one location to another. This is identical to the interpretation offered with
the quasi-geostrophic vorticity equation
When a wind speed asymmetry exists in the vicinity of an upper trough, as shown in the import or export of ……………………………………. can lead to
cyclonic shear vorticity can lead to a net height tendency in the base of the trough
A
B
C
D
E
F
G
The following represents a
digging trough
A
B
C
D
E
F
The following represents a
lifting trough
Digging Trough
In the case where a jet streak is located to the
west of the trough axis
Digging Trough
In the case where a jet streak is located to the west of the trough axis, as in Fig.3a, there is a
net import of cyclonic vorticity into the base of the trough
Digging Trough
In the case where a jet streak is located to the west of the trough axis, as in Fig.3a, there is a net import of cyclonic vorticity into the base of the trough, and we expect
the trough to amplify and dig equatorward toward lower latitudes
In the case where a jet streak is located to the west of the trough axis, as in Fig.3a, there is a net import of cyclonic vorticity into the base of the trough, and we expect the trough to amplify and dig equatorward toward lower latitudes.
Such a trough configuration is commonly referred to as a
“digging” trough
wind speed maximum on the downstream side of the trough leads to
a net export of vorticity
In contrast, a wind speed maximum on the downstream side of the trough leads to a net export of vorticity, leading to a
a weakening and poleward movement of the trough
In contrast, a wind speed maximum on the downstream side of the trough leads to a net export of vorticity, leading to a weakening and poleward movement of the trough; this is known as a
“lifting” trough
A process that is often strongly linked to the amplification or decay of upper- level troughs and ridges is represented by the
differential thermal advection term
A process that is often strongly linked to the amplification or decay of upper- level troughs and ridges is represented by the differential thermal advection term in The QG Height Tendency Eq.
the term involves the
vertical derivative of thickness advection
This term involves the vertical derivative of thickness advection and represents
thickness tendency that would accompany a given sign of temperature advection within an atmospheric layer.
A
B
C
D
E
F
A
B
C
D
E
The images explain
Geopotential height changes associated with the differential thermal advection
Warm advection
Suppose a …………………….. of warm advection is located…………………………..
maximum
near the 700-mb level
If the column experiences net warming due to this process, the
thickness of the layer must increase.
The sign of the height tendency depends on
whether the pressure surface in question lies above or below the level of maximum thermal advection
The sign of the height tendency depends on whether the pressure surface in question lies above or below the level of maximum thermal advection:
- Height raises above the level of maximum warming.
- Height falls below the level of maximum warming.
- For a pressure surface located exactly at the level of maximum thermal advection, the height tendency would be zero.
A similar interpretation applies to ………………….. of cold advection in the …………….
a local maximum
lower troposphere
A similar interpretation applies to a local maximum of cold advection in the lower troposphere (Fig. 4b); only the signs of the height tendency are
reversed relative to those in the warm-advection case
Differential thermal advection of either sign is frequently observed in
the vicinity of midlatitude cyclones
Warm advection to the ………………………………………….. is often associated with
east of such systems (ahead of a warm front)
pressure falls in the lower troposphere and a building of an upper ridge downstream of the system.
Behind the surface cold front to the
west of a cyclone, lower-tropospheric cold advection
Behind the surface cold front to the west of a cyclone, lower-tropospheric cold advection is consistent with
rising surface pressure and falling upper-level geopotential height surfaces.
The role of the diabatic term in Eq.(1) is similar to that of
the thermal advection
Diabatic warming…………………………. increases with ………………
J =dQ/dt
hight
Diabatic warming increasing with height leads to ……………. , implying a ………………………………
x < 0
local decrease in geopotential height with time
Conversely, diabatic warming decreasing with
height (or diabatic cooling increases with height)
Conversely, diabatic warming decreasing with height (or diabatic cooling increases with height), leads to ……… implying a ………………..
x > 0
local increase in geopotential height wind time
the following is the equation of
the QG Height Tendency Eq.
the terms are
- Geostrophic vorticity advection
- Differential thermal advection and
- Differential diabatic heating.
three forcing terms of the GQ height tendency equation
the following equation represents
The contribution to the local geopotential height tendency exclusively due to geostrophic vorticity advection
………………………………………… will result in local decrease in geopotential height with time
Cyclonic geostrophic vorticity advection
……………………………………………………………….. will result in local increase in geopotential height with time
Anticyclonic geostrophic vorticity advection
In an idealized trough/ridge scenario (Fig.1), where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is maximized
in the base of each trough
thus there is an anticyclonic geostrophic vorticity advection to the west of the trough axis, which is associated with a tendency for hight rises
In an idealized trough/ridge scenario (Fig.1), where the geostrophic wind is uniform everywhere and thus geostrophic relative vorticity is minimized
in the apex of each ridge
this, there is a cyclonic geostrophic vorticity advection to the west of the trough axis, which is associated with a tendency for hight falls
………………………………………………. blows parallel to contours of constant geopotential height
the geostrophic wind
……………………………………………………. does not result in the amplification (or intensification) of troughs and ridges
geostrophic absolute vorticity advection
……………………………………………. results in their movement from one location to another
geostrophic absolute vorticity advection
………………………………………………. is identical to the interpretation offered with …………………………………….
geostrophic absolute vorticity advection
the quasi-geostrophic vorticity equation
………………………………………………… can lead to a net height tendency in the base of the trough.
wind speed asymmetry exists in the vicinity of an upper trough
the import or export of cyclonic shear vorticity
…………………………………………………………… is represented by the differential thermal advection term
A process that is often strongly linked to the amplification or decay of upper- level troughs and ridges
the following is
Differential Thermal Advection
