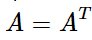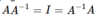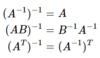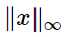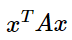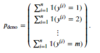Linear Algebra with NumPy Primer Flashcards
(52 cards)
1
Q
What does this mean?
A
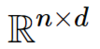
the set of all real-valued matrices with n rows and d columns
2
Q
What is this called? What does it mean?
1(x)
A
- binary indicator function,
- returns 1 if x is a true boolean and 0 otherwise
3
Q
What does this mean?
A
the set of all real-valued n-dimensional vectors
4
Q
What does this mean?
A
the set of real numbers
5
Q
What is this?
A
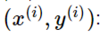
- A pair of input vector and output scalar
- The superscript indicates the index of this pair, not the exponent. In other words, x(5) is the input vector at index 5, not x raised to the power of 5.
6
Q
What is this?
|C|
A
- Determinant if C is a matrix
- Cardinality (number of member elements) if C is a set.
7
Q
What’s a column vector?
A
Each entry occupies one row.
8
Q
What’s this?
A
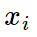
One use: denotes the i-th entry of a column vector
9
Q
What does this mean?
A
Row vector. Each entry covers 1 column
10
Q
For matrix A, what is
A
denotes the i-th row of A
11
Q
For matrix A, what is
A
denotes the i-th column of A
12
Q
What can dot product be applied to? What’s the formula?
A
Two vectors of same dimensions
13
Q
What’s the inner product?
A
Same as dot product
14
Q
- What can outer product be applied to?
- What does it result in?
- What’s the formula?
A
- Vectors (can have different number of elements)
15
Q
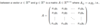
What’s another way to express a dot product for two column vectors x and y?
A
16
Q
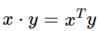
What’s this for two vectors x and y?
A
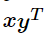
The outer product
17
Q
What’s a matrix-vector product?
A
18
Q
- What are the properties of matrix multiplication? (2)
- What properties does it not have? (1)
A
Matrix multiplication is:
- associative, (AB)C=A(BC)
- distributive, A(B+C)=AB+AC
Is not:
- commutative, AB≠BA
19
Q
What’s a property of transposes?
A
20
Q
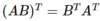
What’s the Hadamard product?
A
elementwise matrix multiplication
21
Q
What does this mean?
A
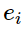
A standard basis vector - ith entry is 1 and the other entries are all 0
22
Q
What does this denote?
A
Identity matrix of nxn size
23
Q
What’s the point of a basis vector?
A
By multiplying a basis vector with a vector x∈Rn, we obtain the single entry xi
24
Q
Describe the idea of one-hot encoding
A
- In each row of the resulting one-hot-encoded matrix:
- In each row of the original vector, find the value
- This value will serve as the column index of the “1” entry in the same row in the corresponding matrix.
- The remaining values in that row are 0
25
What's a symmetric matrix?
26
What's this? What can it be applied to?
* Inverse matrix
* Only applied to square matrices
27
What's the fundamental rule of matrix inverses?
28
What are the properties of matrix inverses?
29
What's a diagonal matrix?
a rectangular matrix with non-zero entries only on the main diagonal
30
What's this?
* The p-norm (a vector norm).
* It's indicative of its magnitude or length
31
What's the formula of this?
32
What's this called? (2)
* L2 norm (aka Euclidean norm):
33
What's this?
Gives the number of non-zero entries in the vector
34
What's this?
gives the maximum magnitude across the entries in vector x
35
What's this? What can it be applied to?
trace(A)
* Sum of the elements across the main diagonal
* Only applied to square matrices
36
* What's this?
* What can it be applied to?
* quadratic form
* See screenshot for applied to
37
What's vectorization?
a style of programming where operations are applied to whole arrays instead of individual elements (i.e. operate on entire data structure instead of loops)
38
When should we use vectorization?
Whenever possible
39
Why are python loops slower than C or Java loops?
* Python performs variable type checks at each loop iteration
40
* What's ndarray?
* What's a characteristic of its data structure?
* Data structure with an interface similar to python lists, but its operations are performed in optimized C code
* A homogeneous data structure
41
What's the runtime complexity of matrix multiplication using the original definition of MM? (optional)
O(n^3)
Description:
Here each entry in AB is the result of the dot product between a row in A and a column in B, which are both n-dimensional vectors. Therefore, it takes roughly n computations to yield one entry in AB, and because there are n2 entries, a total of n3 computations are required.
More formally, we say that the runtime complexity of matrix multiplication is O(n3). This notation indicates the growth rate of matrix multiplication -- if we increase the size of A and B by a factor of 10, we will need (10n)3=1000n3 computations
42
What do we know about the matrix multiplication algorithms of data science libraries?
They use algorithms that are more efficient than the textbook definition of matrix multiplication
43
* What's a condition for vectorization?
* What do we have to do if it's not met?
* What are 3 scenarios that pose this problem?
* the elementwise operations are independent of each other
* If not met, need to revert to using loops
* Problem scenarios (examples in screenshot)
* Loop dependency
* Indirect memory access
* Code branching
44
How do you know if a function is vectorizable?
It doesn't belong to the 3 problem scenarios of the independence condition
45
How do you vectorize a function using numpy?
"register" it through the np.vectorize function.
46
How does the performance of a custom vectorized function compare to alternatives?
Not as fast as functions of same functionality from DS libraries like numpy because they're not executed in optimized C code
47
How do you vectorize an interative function? (4)
1. Given an iterative formula, organize its expected outputs in a suitable vector or matrix format.
2. Break down this vector or matrix into smaller components.
3. Vectorize each component by using matrix and vector operations. Honorable mentions include one-hot encoding, quadratic form, XXT along with XTX, and elementwise operators.
4. Identify the appropriate NumPy functions to convert the vectorized expression into code.
48
With two arrays x and y of the same size, how do you make a new array with some elements from x and some from y based on a condition?
numpy.where(condition, x, y)
where x and y are arrays
Returns an array with elements from x where the condition is True, and elements from y elsewhere.
49
What are honorable mentions changes for when you can't fully vectorize a component? (4)
* one-hot encoding
* quadratic form
* XXT along with XTX
* elementwise operators
50
What should you be thinking when you're trying to vectorized a function and you see this?
This is the same as a one-hot encoding then summing across the rows
51
What's a property of the binary indicator function?
𝟙(𝑎 & 𝑏)=𝟙(𝑎)×𝟙(𝑏).
52
What should you think when you see a vector of dot products?
it very likely comes from a matrix-vector multiplication.
