Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

11637 Foundations of Computational Data Science > numpy Primer > Flashcards

numpy Primer Flashcards

(85 cards)

Start Studying
1
Q

What’s a major benefit of numpy? How does it do this?

A

Efficient manipulation of large datasets. It’s especially useful for high-dimensional array operations.

It does this through:

  • A homogeneous array that allows for faster access
  • Specialized C-based implementations of many operations.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What’s the heart of numpy?

A

The array data structure np.ndarray, which offers many powerful utilities.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What’s the rank of an array?

A

The number of dimensions it has

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What’s the shape of a numpy array? (type, make-up)

A
  • Type: An n-element tuple
  • Make-up: each element denotes the size of an array along a particular dimension.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

How to create an array

A

a = np.array([[1., 2.], [3., 4.]])

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What type are the elements of a numpy array?

A
  • numpy will deduce using the elements passed in
  • If you don’t pass elements in initially (e.g. zeros method), default is float64
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

How do you access an element in a numpy array?

A

[row_index, col_index]

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

How to create a numpy array of a certain constant

A

np.full((2,2), 100)

goes to:

array([[100, 100], [100, 100]])

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

How to create an identity matrix in numpy

A

np.eye( length of side)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

How to create a numpy array of a random sample from a predefined distribution (e.g. normal)?

A

np. random.some_distribution.(size = some_shape_tuple)
np. random.normal(size = (2, 3))

goes to:

array([[-1.41377114, -0.26157494, 0.05751016],

[0.64421317, -0.46843433, -2.47728257]])

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

What do we know about arrays of shape ( some_int, )?

A

They should be thought of as column vectors, since they have multiple rows, but only one column.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

What does the shape (2,) mean? How do you initialize an array of that shape?

A

For example: np.array([1,2])

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What happens when you transpose a 1D array in numpy?

A

Nothing. It will still be a column vector.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

How do you get the shape of a numpy array?

A

.shape

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

How do you transpose a numpy array?

A

.T

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

What’s the syntax for slicing in numpy?

A

Syntax is start_index:end_index. You must specify a slice for each dimension of the array. To take all values in a certain dimension, you can use a standalone : or just leave that dimension blank.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

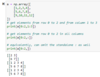
What do we know about how numpy slicing works in memory?

A

It’s a shallow copy? If you make a new array that’s a slice of another array and you modify the new array, it will also modify the original array.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

When mixing integer and slicing indexing, how does slicing vs using integer indexing effect the rank?

A

Each dimension with integer indexing reduces the rank by 1. Using slicing in all dimensions preserves the rank.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What’s integer array indexing?

A

Instead of an index, you put an array of indexes where the index would be. That will get all of the portions or the array corresponding to the specified indexes, and it will combine them into the output array.

E.g. this gets two copies of row 0 in a and three copies of row 1 in a:

a[[0, 0, 1, 1, 1],:]

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

What’s a good way to quickly combine different portions of an input array to form a new output array?

A

integer array indexing

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

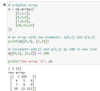
How do you manipulate two elements in a numpy array in one line?

A

Use integer array indexing. E.g.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

What’s boolean array indexing?

A

Can easily test a numpy array with a boolean condition.

a = np.array([[1,2], [3,4], [5,6]])
print(a > 2)

Returns an array of booleans.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

What does this do on multidimensional numpy array a?

print(a[a > 0.9])

A

Returns a rank-1 array of elements that meet the condition. This boolean array indexing is always rank 1.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

How does numpy determine the data type of array elements?

A
  • Numpy will try to guess the data type of an array upon creation, but you can also explicitly specify the data type
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
How do you explicitly specify a datatype in numpy?
z = np.array([1, 2], dtype=np.int64)
26
How do you convert from one datatype to another in numpy?
Use astype. E.g.: print(x.astype(np.float64))
27
How do you element-wise multiply two arrays in numpy?
\*
28
What do we know about binary operator operations in numpy?
the two input arrays must have the same shape (I think after broadcasting, if applicable)
29
How do you raise elements to an exponent in numpy?
\*\*
30
What's np.dot used for? (3) What method type is it?
use np.dot to * compute inner products of vectors * multiply a vector by a matrix * multiply matrices dot is available both as a function in the numpy module and as an instance method of array objects. dot product of v and w print(v.dot(w)) equivalent function to compute dot product print(np.dot(v, w))
31
In which cases should we not use "dot"? (2)
Use these equivalents in these situations: * if both a and b are 2-dimensional arrays, dot is equivalent to matmul or @ * if either a or b is scalar, dot is equivalent to \* (elementwise multiplication),
32
What do we know about 1D arrays in numpy?
Numpy vectors are always treated as column vectors.
33
What do we know about operations that involve both row and column vectors in numpy?
Numpy vectors are always treated as column vectors. Therefore, to perform operations that involve both row and column vectors, we cannot use the typical matrix multiplication operators, but instead need to call the appropriate Numpy function. For example, to compute the outer product 𝑤×𝑤𝑇 , which we expect to be a 2×2 matrix, we can use np.outer
34
How do you sum all elements?
x.sum()
35
How do you sum along the rows?
x.sum(axis = 1)
36
How do you sum along the columns?
x.sum(axis = 0)
37
What is broadcasting?
A process where numpy scales up a smaller array to make operations with an array of a different shape possible. The simplest cases are making operations between a small array and large array possible.
38
What's the process for broadcasting?
* If a and b have different ranks, add one-element dimensions to a or b until they have the same ranks. For example, if a = [[1,2],[3,4]] (2-dimensional) and b = 10 (0-dimensional), we would turn b to 2-dimensional, i.e., [[10]]. * Now that a and b have the same ranks, iterate through each dimension i of a and b: * If the shapes of a and b in dimension i are the same, move on. * Else if the shape of b is 1 in dimension i, we'll copy index 0 of dimension i of b until its shape is the same as that of a. * Else if the shape of a is 1 in dimension i, we'll copy index 0 of dimension i of a until its shape is the same as that of b. * Else, raise "ValueError: operands could not be broadcast together"
39
What does the "None" keyword do?
Same as np.newaxis. This increases the rank of the array by 1
40
What's an alternative to np.outer?
For outer products on vectors, an alternative to np.outer is broadcasting the 1D vectors to 2D matrices and multiplying them as usual. This has the advantage of working with not just outer products, but also any other binary operations.
41
How do you copy an array a certain number of times in any given direction in numpy?
numpy. tile(arr, reps) reps: The number of repetitions of A along each axis.
42
What does np.tile do?
construct a new array by repeating an input array the number of times given by the reps arg
43
What's view and copy?
View: Shallow copy (i.e. shares same address in memory with the input) Copy: Deep copy (i.e. doesn't share memory with the input)
44
Does boolean array indexing return a view or copy?
copy
45
Does integer array indexing return a view or copy?
copy
46
Does slicing return a view or copy?
View
47
What do we know about broadcasting?
Use it wherever we can. It should be preferred whenever possible
48
What do we know about functions that return a view?
functions that return a view typically are very fast because they do not need to allocate new memory.
49
What's one important thing to remember while writing your code?
**Knowing when a copy or a view is returned** is essential in understanding the behavior of your code. Otherwise, you may run into a situation where an array value changes even though you never touch it (but you modified a view of it), which can be difficult to debug.
50
How are numpy arrays represented in memory? What's it similar to?
contiguous one-dimensional segment of computer memory Similar to a C array
51
What's the type policy of numpy arrays?
* Variables all have to be the same type (i.e. it's a homogeneous data structure)
52
What's one interesting characteristic of numpy arrays?
Numpy arrays inherit many attributes of C arrays
53
What happens when you make a heterogeneous numpy array?
* no error is thrown * You are not able to do anything significant with it beyond the functionalities of a standard Python list
54
What do we know about operations that add or remove elements to/from a numpy array? (2)
* Will return a new array, instead of modifying the input in-place * Creating a new array in memory is time-consuming, so these operations **should not be used inside a loop.**
55
What's a sparse matrix?
Matrix which contain mostly zero entries and only a few non-zero entries
56
What does Scipy's sparse matrix library do?
An important advantage of Scipy's sparse matrix: It consumes a lot less memory while being functionally similar to standard Numpy matrices.
57
How should you create a sparse matrix?
Use the coo\_matrix method. 1. Construct 3 lists: value, row index and column index 2. Pass the lists and the shape to the method
58
How should you **not** create a sparse matrix?
Convert a dense matrix to sparse
59
How do you print the dense representation of a sparse matrix?
Use ".A"
60
How do we do an operation on a sparse matrix? Why? What does it return?
* Should be converted to csr\_matrix (compressed sparse row) or csc\_matrix (compressed sparse column) * Because coo\_matrix is slow in row and column access * Returns: 2D sparse matrices, not 1D vectors like what Numpy would return
61
What are the pros (3) and cons (2) of CSR / CSC?
62
What operations are available for CSR matrix and CSC matrix? Why would we use them?
* Standard mathematical transformations (e.g., power, sqrt, sum), as well as matrix operations (dot, multiply, transpose) are available. * They're usually faster
63
If we're working with a scipy sparse matrix and an operation is supported by both scipy.sparse and numpy, which do we use? Why?
* always use the scipy.sparse version * Why: Sometimes the numpy version will convert the sparse matrix input to dense matrix
64
How do we optimize matrix-vector multiplication?
Minimize the amount of times you need to multiple two matrices together. Instead, do as many matrix\*vector operations as possible. Example: * two matrices A,B and a vector x. * (AB)x=A(Bx), but which is faster? * right side is faster because it's 2 matrix\*vector operations instead of 1 matrix\*matrix and 1 matrix\*vector operation
65
What's the best operation for this? Description: Inner product between vectors Setting: Vectors u and v with same shape
u.dot(v)
66
What's the best operation for this? Description: Multiply a matrix with its transpose Setting:
X @ X.T or X.T @ X
67
What's the best operation for this? Description: Outer product between vectors Setting: Vectors u and v
np.outer(u,v)
68
What's the best operation for this? Description: Add a vector to every row of a matrix Setting: Matrix X with shape (m, n), vector u with shape (n,)
X + u
69
What's the best operation for this? Description: Add a vector to every column of a matrix Setting: Matrix X with shape (m, n), vector v with shape (m,)
X + v[:,None]
70
When should you not use a sparse matrix? (2) Why? (2)
* When either: * The underlying data is not sparse * There are operations that break sparsity (e.g. result of operation is not sparse) * Why: * Takes up more space when data is not sparse
71
For what operation is sparse matrix best used?
matrix multiplication
72
How can we tell the rank of a numpy array from the numpy array syntax? E.g. [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
rank = number of opening brackets at the beginning
73
How do you create a numpy array with values that are spaced linearly in a specified interval?
np. linspace numpy. linspace(start, stop, num\_samples\_to\_generate)
74
How do you create this array in numpy? array([0, 1, 2, 3])
np.arange(4)
75
How do you create a numpy array with evenly spaced values within a given interval?
numpy.arange(start, stop, step)
76
What numpy methods are there to create arrays with certain values in the same shape as another array you already have? (4)
* empty\_like * ones\_like * zeros\_like * full\_like
77
Given np array arr=[1, 1, 2], how do you create [4, 4, 4]?
np.full\_like(arr, 4)
78
How do you create a 3x4 numpy array where each element is 6?
np.full((3,4), 6)
79
How do you specify the data type for elements of a numpy array?
dtype=
80
For a numpy array, how do you get array of elements at particular indices?
arr[[indices of dimension 1], [indices of dimension 1]] E.g. this returns a 1-dimensional array of shape (4,): arr[[0, 1, 2, 3], [3, 2, 1, 0]]
81
How should we matrix multiply two 2-D matrices?
matmul or @
82
How should we multiply a scalar with a matrix?
\*
83
How does numpy handle it if your array elements do not conform to numpy's supported data types?
* No error will be thrown * The default data type will be object
84
How does access performance of sparse matrices vs ndarrays compare?
Data access is much slower in sparse matrix than in Numpy matrix:
85
What's the syntax of pandas vectorization?
df[index\_some\_row\_or\_col] = some\_vectorizable\_function(df[some\_row\_or\_col], df[another\_r\_or\_c])

11637 Foundations of Computational Data Science (14 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions