Topic 4: Descriptive Statistics III Flashcards
(20 cards)
Name measures of variation.
- Range
- Variation
Variation
Degree at which score differ from one another of from central tendency.
Range
The range is one measure that allows us to know the variation of data.
Range = X_max - X_min
What is one advantage of Range?
a disadvantage?
- Very easy to compute
- sensitive to the size of the sample
Mean deviation
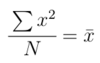
What happens if you add all the deviation scores?
You get 0
What should you do to get the mean of deviation scores?
You should square every deviation score before adding them up.
Sample variance
There is two kinds of sample variance:
-biased and unbiased
What does it mean for a sample variance to be unbiased?
It means that the variance is the same a the parameter. Therefore, it reflects the population.
Variance
Mean of squared deviations scores ( mean square)

Standard deviation
Is the square root of the variance.

Use up to 2 decimal points.
Standard deviation from a frequency table
1) Find the mean by doing
mean = (sum f*X_mid)/N
where X_mid = (up - low)/2
2) Find variance but multiply every (X-mean)^2 times f
3) square root the variance to get the standard deviation
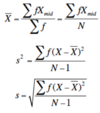
Do example in page 19 of notes
True of false
In a frequency table, if you have a column with all
(X_mid - mean)
the sum of every entry in the column will be 0.
False
Standard Scores
(z-scores)
Number of standard deviations from mean

By dividing by s, one can normalize or scale deviation
scores into standard deviation units.
What does this mean?
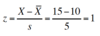
It means that X is 1 standard deviation away from the mean.
What are the units of the z-scores
They have the same units as the standard deviation.

True or False
z-scores can standardize raw data whose Mean = 0, and Standard deviation = 1
True

Do exercise in slide 15, topic 4


