Wahrscheinlichkeitsfunktionen und Wahrscheinlichkeitsdichtefunktionen

Question 1

Motivation Wahrscheinlichkeits- u. Wahrscheinlichkeitsdichtefunktionen

Answer 1

Wenn wir eine konkrete Wahrscheinlichkeitsverteilung Px angeben wollen, müssen wir die Wahrscheinlichkeit P_x(A_x) für jedes Ereignis A_x aus der Ereignismenge angeben.

Problem:

• für diskreten ZV meistens extrem aufwendig (Größe d. Ereignismenge)
• für stetigen Variablen unmögl. (Explizite Angabe aller Elementarereignisse nicht einmal mögl.)

→Angabe einer Funktion mit Hilfe derer die Wahrscheinlichkeiten aller Ereignisse A_x berechnet werden können

• Für diskrete ZV: Wahrscheinlichkeitsfunktion
• Für stetige ZV: Wahrscheinlichkeitsdichtefunktion

Question 2

Definition Wahrscheinlichkeitsfunktion f

Answer 2

Funktion, die jedem Element x_j des Trägers T_x die Wahrscheinlichketi P(X=x) des entsprechenden Elementarerereignisses zuordnet.

Formale Definition:

f: T_x ⟶ℝ

x_j ⟶f(x_j)=P(X=x_j)

• Darstellung i.d.R. in Balkendiagrammen
• (Motivation: Wahrscheinlichkeitsverteilung einer diskreten ZV angeben:)

Allgemein kann man für stetige ZV die Wahrscheinlichkeit für jedes beliebige Ereignis A_x aus der Summe der Wahrscheinlichkeiten der Elementarereignisse berechnen, aus denen sich dieses Ereignis A_x zusammensetzt (3. Kolmogorov- Axiom; Px({x₁, x₂}) = P_x({x₁∪x₂}) = P_x({x₁})+P_x({x₂}); gilt für beliebig viele Wahrscheinlichkeiten von Elementarereignissen)

→

Question 3

(Beispiel Berechnung der Wahrscheinlichkeit P_x(A_x) beliebiger Ereignisse A_x mit Hilfe der Wahrscheinlichkeitsfunktion)

Answer 3

Question 4

Eigenschaften von Wahrscheinlichkeitsfuntionen

Answer 4

Question 5

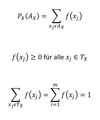
Definition Wahrscheinlichkeitsdichtefunktion

Answer 5

Funktion, deren Integral für jedes Ereignis die Wahrscheinlichkeit dieses Ereignisses angibt:

P_x(A_x)= ∫ f(x)dx

^Ax

Formale Definition:
f: Tx⟶ℝ

x⟼f(x)​

• (Motivation: Wahrscheinlichkeitsverteilung P_x stetiger ZV angeben:)
• Idee d. Wahrscheinlichkeitsfunktion hilft uns nicht weiter (Ereignisse hier häufig Intervalle: nicht als (endliche) Vereinigungsmenge v. Elementareireignissen darstellbar)
• Der Funktionswert f(x) entspricht nicht der Wahrscheinlichkeit des Elementarereignisses {x} (im Gegensatz zur Wahrscheinlichkeitsfunktion)

→ f(x) wird Wahrscheinlichkeitsdichte der Realisation x genannt: kann auch Werte größer als 1 annehmen, besitzt keine intuitive Interpretation

Question 6

(Beispiel Berechnung der Wahrscheinlichkeit Px(A_x) eines beliebigen Ereignisses einer stetigen ZV mit Hilfe der Wahrscheinlichkeitsdichtefunktion und der Formel

P_x(A_x)=∫ f(x),

^Ax

also durch Berechnung der Fläche unter der Wahrscheinlichkeitsdichtefunktion)

Answer 6

Question 7

Eigenschaften von Wahrscheinlichkeitsdichtefunktionen

Answer 7

(analog zu Eigenschaften von Wahrscheinlichkeitsfunktionen)

-Anmerkung: Die letzte Eigenschaf bedeutet, das die gesamte Fläche unter einer Wahrscheinlichkeitsdichtefunktion 1 ergibt (Die Wahrscheinlichkeit dass sich die ZV in dem größten Wert x oder einem kleineren realisiert ist 1)

Question 8

Definition Verteilungsfunktion

Answer 8

Funktion, die jedem Element x des Trägers T_x der ZV die Wahrscheinlichkeit zuordnet, dass sich die ZV in diesem Wert x oder einem kleineren Wert realisiert

Formale Definition:

F: T_x ⟶ℝ

x ⟼F(x)= P(X≤x)

• sowohl für diskrete als auch für stetige ZV definiert

Question 9

3 Bemerkungen Verteilungsfunktion

Answer 9

• I: wird auch kumulative Verteilungsfunktion genannt
• II: Der (kleinste) Wert x, für den P(X=x)= p ist, wird auch p-Qunatil der ZV genannt
• III: Bei Kenntniss der Verteilungsfunktion kann, ähnlich wie bei der Wahrscheinlichkeitsfunktion oder der Wahrscheinlichkeitsdichtefunktion, die Wahrscheinlichkeit P_x(A_x) für jedes Ereigniss A_x berechnet werden

Question 10

Verteilungsfunktion und Wahrscheinlichkeitsfunktion

Answer 10

Im Fall einer diskreten ZV X besteht folgender Zusammenhang zwischen der Verteilungsfunktion F und der Wahrscheinlichkeitsfunktion f:

• Bemerkung: der Zsm.hang zw. F und f bei diskreten ZV ist sehr ähnlich wie der Zsm. zw. kummulierten relativen Häufigkeiten und relativen Häufigkeiten in der Deskriptivstatistik

Question 11

Verteilungsfunktion und Wahrscheinlichkeitsdichtefunktion

Answer 11

• Im Fall einer stetigen ZV besteht folgender Zsm.hang zw Verteilungsfuntion F und Wahrscheinlichkeitsdichtefunktion f:

Question 12

(Beispiel Verteilungsfunktion einer diskreten ZV)

Answer 12

Question 13

(Beispiel Verteilungsfunktion einer stetigen ZV: Darstellung)

Answer 13

Question 14

(Beispiel Verteilungsfunktion einer stetigen ZV)

Answer 14

Question 15

(Beispiel Verteilungsfunktion einer stetigen ZV: graphische Darstellung)

Answer 15