Week 10

Question 1

Find the derivative of the following functions by first principals (i.e. using the definition of the derivative).

y= 2x−5

Answer 1

Question 2

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative).

y= 5x²

Answer 2

Question 3

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative)
y= 4x−3x²

Answer 3

Question 4

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative).

y=x²−2x+√7

Answer 4

Question 5

Find dydx for each of the following functions

y= 4x−7

Answer 5

Question 6

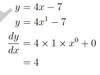
Find dydx for each of the following functions.

y=−7x+ 2

Answer 6

Question 7

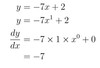
dydx

y= 3x²−4x+ 8

Answer 7

Question 8

dydx

y= 5x³−8x²+ 9x+ 1

Answer 8

Question 9

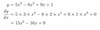
dydx

y=−6x⁴+ 10x³

Answer 9

Question 10

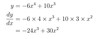
dydx

y= 6 sin(x) +x²

Answer 10

Question 11

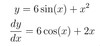
dydx

y= 9 cos(x)−3 sin(x)

Answer 11

Question 12

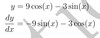
dydx

y=−4 cos(x) + 7 sin(x)

Answer 12

Question 13

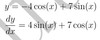
dydx

y=e^3x+ 4

Answer 13

Question 14

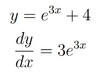
dydx

y= 6e^2x+x²

Answer 14

Question 15

dydx

y= 10e^−5x

Answer 15

Question 16

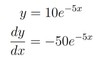
dydx

y= 2 ln(x)

Answer 16

Question 17

dydx

y=−4 ln(x)

Answer 17

Question 18

dydx

y=−7 ln(x) + 4

Answer 18

Question 19

dydx

y=4/x2

Answer 19

Hint: At first glance, it may not appear asthough the functions below match the table of derivatives. You may first need to rewrite the function so that it matches the table of derivatives.

Question 20

dydx

y=−3√x

Answer 20

Hint: At first glance, it may not appear asthough the functions below match the table of derivatives. You may first need to rewrite the function so that it matches the table of derivatives.

Question 21

dydx

y= 1/e^2x

Answer 21

Hint: At first glance, it may not appear asthough the functions below match the table of derivatives. You may first need to rewrite the function so that it matches the table of derivatives.

Question 22

dydx

y= 5 ln(x²)

Answer 22

Hint: At first glance, it may not appear asthough the functions below match the table of derivatives. You may first need to rewrite the function so that it matches the table of derivatives.

Question 23

Consider the function

f(x) = 2x³+ 3x²−36x+ 12

where −6 ≤ x ≤ 4.

Determine the greatest and least values for f(x).

Answer 23

Question 24

Consider the function

f(x) =−x²+ 6x

(a) Find the equation of the tangent to the function

f(x) at x= 2.

Answer 24

Question 25

Consider the function f(x) =−x²+ 6x (b) Find the equation of the tangent to the function f(x) at y= 5. (Note that there willbe two tangents so you will require an equation for each tangent).

Answer 25

(b) We have been asked to find the equation of the tangent line when y= 5. The first step is to find the corresponding x values. 5 =−x²+ 6x x²−6x+ 5 = 0 (x−1)(x−5) = 0 x= 1 or x= 5 We will find the tangent line for x= 1 first. When x= 1, y = −1²+ 6×1 = 5 When x= 1, dydx = 4 Therefore the tangest line at x= 1 has a gradient of 4 and passes through the point (1,5). y−y1=m(x−x1) y−5 = 4(x−1) y−5 = 4x−4 y= 4x+ 1 Now we will find the tangent line for x= 5. When x= 5, y = −5²+ 6×5 = 5 When x= 5, dydx = −4 Therefore the tangest line at x= 5 has a gradient of −4 and passes through the point (5,5). y−y1 = m(x−x1) y−5 = −4(x−5) y−5 = −4x+ 20 y = −4x+ 25 Therefore, the tangent lines when y = 5 are y = 4x+ 1 and y = −4x+ 25.

Question 26

Consider the function f(x) =−x²+ 6x (c) Find the equation of the tangent to the function f(x) at the x-intercept. (Similar to part (b), there will be two tangents)

Answer 26

We have been asked to find the equation of the tangent line when the curve cuts the x-axis. −x²+ 6x= 0 x(−x+ 6) = 0 x= 0 or x= 6 We will find the tangent line for x= 0 first. When x= 0, y = −0²+ 6×0 = 0 When x= 0, dydx = 6 Therefore the tangest line at x= 0 has a gradient of 6 and passes through the point (0,0). y−y1=m(x−x1) y−0 = 6(x−0) y= 6x Now we will find the tangent line for x= 6. When x= 6, y = −6²+ 6×6 = 0 When x= 6, dydx = −6 Therefore the tangest line at x = 6 has a gradient of−6 and passes through the point (6,0). y−y1=m(x−x1) y−0 =−6(x−6) y=−6x+ 36 Therefore, the tangent lines where the curve cuts the x-axis are y = 6x and y = −6x+ 36.

Question 27

The population of a colony of seagulls can be modelled by G(t) = 20t(9−t²) + 450 where G(t) is the number of seagulls and t is number of months since the research project began and 0 ≤ t ≤ 3. (a) Determine the number of seagulls in the colony at the start of the research project.

Answer 27

G(t) = 20t(9−t²) + 450 (a) The initial population is when t= 0. G(0) = 20×0×(9−0²) + 450 = 450 There was initially 450 seagulls.

Question 28

The population of a colony of seagulls can be modelled by G(t) = 20t(9−t2) + 450 where G(t) is the number of seagulls and t is number of months since the research project began and 0 ≤ t ≤ 3. (b) Calculate the rate of change of seagulls one month after the start of the research project.

Answer 28

Question 29

The population of a colony of seagulls can be modelled by G(t) = 20t(9−t²) + 450 where G(t) is the number of seagulls and t is number of months since the research project began and 0 ≤ t ≤ 3. (c) What was the seagull population at the end of the research project?

Answer 29

G(3) = 20×3(9−3²) + 450 = 450 There were 450 seagulls at the end of the research project.

Question 30

The population of a colony of seagulls can be modelled by G(t) = 20t(9−t²) + 450 where G(t) is the number of seagulls and t is number of months since the research project began and 0 ≤ t ≤ 3. (d) Determine the greatest population of seagulls during the research project.

Answer 30

Question 31

Oil is spilling from an oil rig at sea and has created a circular oil patch on the water. (a) Construct a function A(r) that models the oil spill where A(r) is the area of the oilpatch with a radius of r.

Answer 31

The equation for the oil spill is A(r) =πr² where A(r) is the area of the oil spill and r is the radius of the oil spill.

Question 32

Oil is spilling from an oil rig at sea and has created a circular oil patch on the water. (b) Find the rate at which the area of the oil patch is increasing with respect to the radius of the oil patch.

Answer 32

Question 33

Oil is spilling from an oil rig at sea and has created a circular oil patch on the water. (c) Calculate the rate at which the area of the oil patch is increasing when its radius is 15 metres.

Answer 33

Question 34

(Harder) Tangents are drawn to the curve y=x²+ 5x−6 at the points where the curve intersects the x-axis. Where do the two tangents intersect?

Answer 34

y=x²+ 5x−6 dydx = 2x+ 5 To begin, we need to find the x values of the tangent lines. When the curve cuts the x-axis, y= 0. x²+ 5x−6 = 0 (x+ 6)(x−1) = 0 x=−6 or x= 1 We will start by finding the tangent line at x = −6. When x = −6, dydx = −7 Therefore, the tangent line at x = −6 has a gradient of −7 and passes through the point (-6,0) y−y1=m(x−x1) y−0 =−7(x−−6) y=−7(x+ 6) y=−7x−42 We will now find the tangent line at x= 1. When x= 1, dydx = 7 Therefore, the tangent line at x = 1 has a gradient of 7 and passes through the point (1,0) y−y1=m(x−x1) y−0 = 7(x−1) y= 7x−7 Therefore, the equations of the tangents when the curve cuts the x-axis are y=−7x−42 y= 7x−7 To find where the two tangents intersect, we need to solve the simultaneous equations above. This gives −7x−42 = 7x−7 14x=−35 x=−2.5 Substituting x = −2.5 into the first equation gives y = −7×−2.5−42 = −24.5 Therefore, the two tangent lines intersect at x = −2.5, y = −24.5