Week 7 Complete Flashcards

Question 1

Q

Linear Functions can be written in 2 ways

Answer

A

Standard form: 𝑎𝑥+𝑏𝑦+𝑐=0

Gradient-Intercept form: y=𝑚𝑥+𝑐

Question 2

Q

Write 𝑦=3𝑥+2 in standard form

Answer

A

𝑦=3𝑥+2 𝑦=3𝑥+2(−𝑦) 0=3𝑥−𝑦+2 or 3𝑥−𝑦+2=0

Question 3

Q

The gradient intercept form is so called because

Answer

A

if 𝑦=𝑚𝑥+𝑐 then the gradient of the line is 𝑚 and 𝑐 is the 𝑦 value where the line cuts the y axis.

Question 4

Q

slope is also called the gradient, which is calculated by?

Answer

A

rise/run **(y/x)**

Question 5

Q

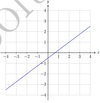
linear function? form

Answer

A

y=mx+c 𝑦=(3/2)𝑥+(1)

Question 6

Q

dissect linear function form

Answer

A

y=(3/2)x+1 3/2 = gradient/slope = m 1 = y-int = c

Question 7

Q

y=(3/2)x+1

x intercept (at y = 0)

Answer

A

y=(3/2)x+1

x intercept (at y = 0)

0=(3/2)x+1

1 = (3/2)x
2/3 = x

Question 8

Q

y=(3/2)x+1

y intercept (at x = 0)

Answer

A

y=(3/2)x+1

y intercept (at x = 0)

y=(3/2)(0)+1 y=1

Question 9

Q

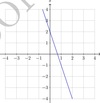
Graph 4𝑥+2𝑦−5=0

using the gradient and y-intercept.

Answer

A

4𝑥+2𝑦−5=0

2𝑦−5 =−4𝑥

2y/2= - 4x/2 +5/2

y= -2x + 2 1/2

m = -2 = - 2/1

(means graph will drop from left to right)

y-intercept = 2 1/2

i.e. (0,2 1/2)

Question 10

Q

Special Linear Equations

There are 2 straight lines that don’t quite fit the form of:

𝑎𝑥+𝑏𝑦+𝑐=0

or

𝑦=𝑚𝑥+𝑐.

Answer

A

𝑥=𝑎
e. g.

𝑥=3 (or 𝑥−3=0)

This means every point on this line, 𝑥 must be 3.

𝑦=𝑏
e. g.

𝑦=−2(or 𝑦+2=0)

Likewise, every point on this line 𝑦 must equal −2.

Question 11

Q

the line is positive if it rises from the:

and negative if it rises from the:

Answer

A

positive if Left to Right

negative if Right to Left

Question 12

Q

Question 13

Q

Another method for plotting the graph:
𝑦 = 3/2𝑥 + 1

Question 14

Q

Finding the equation of lines, given one point and the gradient.
Sometimes we know a line passes through a given point and we know the gradient, hence
we can find the equation of this line. This requires the rule:

Answer

A

𝒚 - 𝒚₁ = 𝒎(𝒙 - 𝒙₁)

where (𝑥₁, 𝑦₁) is the point the line passes through and 𝑚 is the gradient

Question 15

Q

Find the equation of the line that passes through (-3,4) with a gradient of 2

Answer

A

(-3,4) with a gradient of 2

(𝑥₁, 𝑦₁) ↔ (-3,4) (i.e. 𝑥₁ = -3, 𝑦₁ = 4)
𝑚 = 2
𝑦 - 𝑦₁ = 𝑚(𝑥 - 𝑥₁)
𝑦 - 4 = 2(𝑥 - (-3))
𝑦 - 4 = 2(𝑥 + 3)
𝑦 - 4 = 2𝑥 + 6
𝒚 = 𝟐𝒙 + 𝟏𝟎
Check: (because (-3,4) lies on this line, when we substitute in 𝑥 = -3 we should get 𝑦 = 4)
𝑦 = 2 × (-3) + 10
𝑦 = -6 + 10
𝑦 = 4
Also 𝑦 = 2𝑥 + 10 has a gradient of 2

Question 16

Q

Find equation of lines through 2 points.
If we know 2 points, we can find gradient, then use 𝑦 - 𝑦₁ = 𝑚(𝑥 - 𝑥₁)
Example: Find the equation of the line that passes though (-3,4) and (2, -1)

Answer

A

Solution: Although its not necessary, we may find it useful to quickly sketch the 2 points on
the Cartesian Plane. The gradient of the line joining 2 points (𝑥₁, 𝑦₁) and (𝑥₂, 𝑦₂)

is

m=y₂-y₁/x₂-x₁

(rise/run)

Question 17

Q

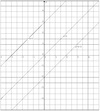
Parallel lines have the same gradient.

Answer

A

𝑦 = 3𝑥 - 2 𝑦 = 3𝑥 + 1 6𝑥 - 2𝑦 + 5 = 0
all have a gradient of 3 and when sketched will be parallel to each other

Question 18

Q

Find the equation of the line passing though (-4, -2) which is parallel to
3𝑥 - 5𝑦 + 8 = 0

Answer

A

Solution: We know parallel lines have the same gradient, so we need to find the gradient of
the given line.

Question 19

Q

𝑦 = 𝑚₁𝑥 + 𝑐₁

𝑦 = 𝑚₂𝑥 + 𝑐₂

product of gradient? perpendicular

Answer

A

𝑚₁ × 𝑚₂ = -1

because they are perpendicular, always -1

Question 20

Q

Find equation of line through (3,4) that is perpendicular to the line
𝑦 =2/5 𝑥 - 1

Question 21

Q

If 2 lines are not parallel to each other

Answer

A

then they will intersect each other at one point (𝑥, 𝑦)
only.
Point of Intersection or the Simultaneous
Solution.
There are 2 methods of finding this
unique solution, Substitution and
Elimination.

Question 22

Q

Solve

3𝑥 + 2𝑦 - 6 = 0
and

2𝑥 - 𝑦 + 10 = 0

by substitution

Answer

A

The substitution method entails rearranging one of the equations to get either 𝑥 or 𝑦 by itself
and then substituting that value into the other equation.

Solution:

3𝑥 + 2𝑦 - 6 = 0 –(1)
2𝑥 - 𝑦 + 10 = 0 –(2)
Number both equations, and make sure
both are in the form 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0

Upon inspection we can see that in equation (2) it can be easily rearranged to make 𝑦 the
subject.

(2)→ 2𝑥 + 10 = 𝑦 –(2a)

Now substitute for 𝑦 in equation (1)

(1)→ 3𝑥 + 2(2𝑥 + 10) - 6 = 0
3𝑥 + 4𝑥 + 20 - 6 = 0

7𝑥 + 14 = 0
7𝑥 = -14
𝑥 = -2

Now substitute for 𝑥 = -2 in (2a)
2𝑥 - 2 + 10 = 𝑦

6 = 𝑦

Answer:

𝒙 = -𝟐
𝒚 = **6**

Question 23

Q

The Elimination method involves

Answer

A

adding or subtracting the equations

Question 24

Q

Solve

2𝑥 + 7𝑦 = 16

and

3𝑥 - 6𝑦 = 2

by elimination

Answer

A

write each equation in standard form

2𝑥 + 7𝑦 - 16 = 0 –(1)
3𝑥 - 6𝑦 - 2 = 0 –(2)

We need to make the co-efficients of either 𝑥 or 𝑦 the same

(1) × 3 6𝑥 + 21𝑦 - 48 = 0 –(1a)
(2) × 2 6𝑥 - 12𝑦 - 4 = 0 –(2a)
(1a) – (2a) 33𝑦 - 44 = 0

33y = 44

y = 44/33 = 4/3

Sub for 𝑦 = 4/3
in either (1) or (2) to find 𝑥

in (1) 2x+7*4/3 -16=0

2x+28/3 - 48/3 = 0

2x=20/3

x=10/3

Answer:

x = 10/3

y = 4/3

Question 25

Q

Solutions to Quadratic Equations

Quadratic functions can be written

𝑦=𝑎𝑥²+𝑏𝑥+𝑐

y as a function of x

Answer

A

y = ax²+bx+c

[If 𝑎 = 0, then 𝑦 = 𝑏𝑥 + 𝑐 and this is a linear equation or function, so not quadratic.]

Now 𝑦 is a function of 𝑥, i.e. 𝑦 = 𝑓(𝑥)
Hence a quadratic can also be written 𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐

Question 26

Q

Graphing Quadratics:

Let’s graph 𝑦=𝑥²+2𝑥−3

Answer

A

This is the shape of the parabola. All quadratics take this shape.

It is symmetrical (a mirror
image) on either side of 𝑥 = -1

Note that the y-intercept is -3.
Recall from work on linear functions, that with all functions
𝑥 intercept is when 𝑦 = 0
𝑦 intercept is when 𝑥 = 0

𝑦 = 𝑥²+ 2𝑥 - 3
𝑦 int. (𝑥 = 0) 𝑦 = 0² + 2 × 0 - 3
So the 𝑐 value still gives the 𝑦 intercept

The 𝑥 intercept is when 𝑦 = 0
0 = (𝑥 + 3)(𝑥 - 1)
Either 𝑥 = -3 or 𝑥 = 1
and these are the 2 points where the graph intersects the 𝑥 axis.
The line of symmetry is 𝑥 = - 𝑏/2𝑎
for 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐

In 𝑦 = 𝑥2 + 2𝑥 - 3, 𝑎 = 1, 𝑏 = 2, 𝑐 = -3
𝑥 = -2/2×1
= -2/2
= -1

We can also find the Turning Point of the parabola, i.e. then point where the function has the
greatest or the least value. For this example, it will be the least or minimum value.
Because 𝑥 = -1 is the line of symmetry, then the least value of the function 𝑦 = 𝑥² + 2𝑥 - 3
will occur at 𝑥 = -1

Substitution 𝑥 = -1 into this equation gives
𝑦 = (-1)² + 2 × (-1) - 3 = 1 - 2 - 3 = -4

So the Turning point is (-1, -4), as can be seen in the previous graph and the minimum
value of the function is -4

Question 27

Q

Sketch the graph

𝑦=−9+6𝑥−𝑥²

showing all 𝑥 and 𝑦 intercepts. As well state the Domain and Range of this function

Answer

A

Line of symmetry

𝑥=−𝑏/2𝑎

𝑥=−6/2×−1=3

When 𝑥=3,

AND 𝑦=−9+6×3−3² = −9+18−9 = 0

So this quadratic only cuts the 𝑥 axis once at 𝑥=3.

Note that the parabola is upside down. When “𝑎” or the coefficient of 𝑥² is negative, the parabola is always upside down

Domain of 𝑦=−9+6𝑥−𝑥²

All possible Real 𝑥 values

−∞<𝑥<∞

Range: The greatest value 𝑦 can take is 0, which occurs at the Turning Point.

−∞<𝑦≤0

Question 28

Q

The Discriminant

Answer

A

𝑏² - 4𝑎𝑐 in the Quadratic Formula is called the Discriminant. By calculating 𝑏² - 4𝑎𝑐, we can
determine how many times the quadratic function cuts the 𝑥 axis.

Question 29

Q

The number (𝑁) of motorists detected speeding on the M1 𝑑 days
(1 ≤ 𝑑 ≤ 10) after the installation of a speed camera can be modelled by the
equation: 𝑁(𝑑) = 𝑑<sup>2</sup>/2 - 3𝑑 + 75

Find

a) When least speeding violations occur
b) When most speeding violations occur

Answer

A

𝑎 = 1/2, 𝑏 = -3, 𝑐 = 75
Line of symmetry
𝑑 = - 𝑏/2𝑎
𝑑 = - -3/2×1/2
= 3
𝑁(3) = 3²/2 - 3 × 3 + 75
𝑁(3) = 4 1/2 - 9 + 75 = 70 1/2

So (3, 70 1/2) is the Turning Point.

Sub in the end values of 𝑑, i.e 𝑑 = 1, 𝑑 = 10
𝑑 = 1 𝑁(1) = 1²/2 - 3 × 1 + 75

= 1/2 - 3 + 75

= 72 1/2

𝑑 = 10 𝑁(10) = 10²/2 - 3 × 10 + 75

= 50 - 30 + 75

= 95

*a) Least violations on day 3 (70 1/2)
b) Most violations on day 10 (95)**

Question 30

Q

A ball is thrown vertically upwards such that its height (metres) above the ground is:

ℎ(𝑡) = 40𝑡 - 5𝑡²

where 𝑡 is the number of seconds after it is thrown

Find:

a) The maximum height reached
b) The times when it is 15m high

c) The time taken to hit the ground

Answer

A

a) Axis of symmetry 𝑡 = - 𝑏/2𝑎

-40/2×-5
=
-40/-10
= 4
At 𝑡 = 4, Turning Point occurs.
Sub in ℎ(𝑡)

ℎ(4) = 40 × 4 - 5 × 4<sup>2</sup>
ℎ(4) = 160 - 80 = 80m

b) ℎ = 15

so 15 = 40𝑡 - 5𝑡²
5𝑡² - 40𝑡 + 15 = 0

÷ 5 𝑡² - 8𝑡 + 3 = 0
𝑎 = 1, 𝑏 = -8, 𝑐 = 3
𝑡 = -𝑏±√𝑏²-4𝑎𝑐/2𝑎
𝑡 = 8±√(-8)²-4×1×3/2×1
𝑡 = 8±√64-12/2
= 8+√52/2
or
8-√52/2
𝑡 = 7.61secs or 0.39secs

c) ℎ = 0

0 = 40𝑡 - 5𝑡²
0 = 5𝑡(8 - 𝑡)
𝑡 = 0 or 𝑡 = 8
𝑡 = 0 corresponds to when the ball is thrown
So 𝑡 = 8 or 8 seconds before it hits the ground

Question 31

Q

Linear and Quadratic Functions are examples of functions called?

Answer

A

polynomials.

Linear:

𝑓(𝑥) = 𝑚𝑥 + 𝑐

𝑚 ≠ 0

Quadratic:

𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐

𝑎 ≠ 0

Cubic:

𝑓(𝑥) = 𝑎𝑥³ + 𝑏𝑥² + 𝑐𝑥 + 𝑑

𝑎 ≠ 0

Quartic:

𝑓(𝑥) = 𝑎𝑥⁴ + 𝑏𝑥³ + 𝑐𝑥² + 𝑑𝑥 + 𝑒

𝑎 ≠ 0

Question 32

Q

Graphical Transformation
It is possible to change the shape and position of a function by?

Answer

A

changing the co-efficients of 𝑥 and the constant term

Question 33

Q

Linear Transformation
Consider graphs of the form 𝑦 = 𝑚𝑥 + 𝑐 (𝑐 = 0). They will all pass through the origin (0,0)

Answer

A

𝑚 = 1 𝑦 = 𝑥

will pass through origin at 45˚
𝑚 = 2 𝑦 = 2𝑥

Is twice as steep

𝑚 = 1/2 𝑦 = 1/2x

Is half as steep

and so on
𝑚 = -1 𝑦 = -𝑥

will pass through origin from negative direction (i.e. top
left at 45˚

𝑚 = -2 𝑦 = -2𝑥

Is twice as steep as 𝑦 = -𝑥
𝑚 = -1/2 𝑦 = -1/2𝑥

Is half as steep

Question 34

Q

The value of 𝑐 moves the line vertically. Start with 𝑦 = 𝑥

Answer

A

𝑦 = 𝑥 + 3

is parallel to

𝑦 = 𝑥

and moved units 3 up on the y axis
𝑦 = 𝑥 - 2 moves 𝑦 = 𝑥 2 units down

Question 35

Q

Sketch 𝑦 = -2𝑥 + 3 showing all transformations from 𝑦 = -𝑥

Answer

A

𝑦 = -2𝑥
3 units up 𝑦 = -2𝑥 + 3

Question 36

Q

Transformations of Quadratics
Let’s start with a simple quadratic, 𝑦 = 𝑥²

Answer

A

𝑦 = 2𝑥²

is twice as steep

𝑦 = 1/2**𝑥²

is half as steep

Now

𝑦 = -𝑥²

and

𝑦 = -2𝑥²

and

𝑦 = -1/2**𝑥²

Question 37

Q

We can move these quadratic graphs vertically

Answer

A

by adding and subtracting values

Adding 2 to 𝑦 = 2𝑥² moves 𝑦 = 2𝑥²
2 units up the y axis

𝑦 = 2𝑥² + 2

Subtracting 3 from 𝑦 = 2𝑥² gives
𝑦 = 2𝑥² - 3 and the graph moves 3
units down the y axis

Question 38

Q

Show all transformations, starting with 𝑦 = 𝑥²,

to sketch 𝑦 = - 1/3**𝑥² - 2

Answer

A

𝑦 = 𝑥²
𝑦 = 1/3**𝑥²
𝑦 = - 1/3**𝑥²
𝑦 = - 1/3**𝑥² - 2

Question 39

Q

Horizontal Transformations
To move 𝑦 = 𝑥²
a) 2 units to right?
b) 3 units to left

Answer

A

a) y = (x - 2)²
b) 𝑦 = (𝑥 + 3)²

Question 40

Q

The graph 𝑦 = (𝑥 - 1)² + 4

Answer

A

𝑦 = 𝑥²
𝑦 = (𝑥 - 1)²
𝑦 = (𝑥 - 1)² + 4

Question 41

Q

Write in standard from

y = 3/5x + 2

Answer

A

y = 3/5x + 2

3/5x - y + 2 = 0

3x - 5y + 10 = 0

Question 42

Q

Write in gradient-intercept from

3𝑥 - 2𝑦 + 5 = 0

Answer

A

3𝑥 - 2𝑦 + 5 = 0

2y = 3x + 5

y = 3/2x + 5/2

Question 43

Q

Write in gradient-intercept from

𝑥 + 3𝑦 - 8 = 0

Answer

A

𝑥 + 3𝑦 - 8 = 0

3y = -x + 8

y = -1/3**x + 8/3

Question 44

Q

state the gradient and y intercept

2𝑥 - 3𝑦 - 1 = 0

Answer

A

2x - 3y - 1 = 0
3y = 2x - 1
y = 2/3**x - 1/3

Question 45

Q

state the gradient and y intercept

𝑦 + 3𝑥 = 4

Answer

A

y + 3x = 4
y = -3x + 4

Question 46

Q

state the gradient and y intercept

y = 6

Answer

A

y = 6
y = 0x + 6

Question 47

Q

Sketch each of these functions showing the 𝑥 and 𝑦 intercepts

a) 𝑦 = 4𝑥 - 8

Answer

A

x-intercept is 2, y-intercept is -8, gradient is 4

Question 48

Q

Sketch each of these functions showing the 𝑥 and 𝑦 intercepts

b) 3𝑥 - 4𝑦 - 2 = 0

Answer

A

3𝑥 - 4𝑦 - 2 = 0

y = 3x/4 - 1/2

x int 2/3, y int -1/2, gradient 3/4

Question 49

Q

Sketch each of these functions showing the 𝑥 and 𝑦 intercepts

2x + y + 1 = 0

Answer

A

2x + y + 1 = 0

y = -2x - 1
x-intercept is -1/2

y-intercept is -1

gradient is -2

Question 50

Q

Sketch each of these functions showing the 𝑥 and 𝑦 intercepts

𝑦 = -3𝑥 + 2

Answer

A

x-int 2/3

y-int 2

gradient -3

Question 51

Q

Find the equation of the line that

a) passes through (-1,4) with gradient 3

Answer

A

y - y₁ = m(x - x₁)
y - 4 = 3(x + 1)
y - 4 = 3x + 3
y = 3x + 7

Question 52

Q

Find the equation of the line that

b) passes through (2, -3) with gradient -1

Answer

A

y - y₁ = m(x - x₁)
y + 3 = -1(x - 2)
y + 3 = -x + 2
y = -x - 1

Question 53

Q

Find the equation of the line that

c) passes through (-3,1) and (4, -5)

Answer

A

We will start by finding the gradient, m, of the line.

m = y2-y1/x2-x1

m = -5-1/4+3

m = -6/7

Now we can find the equation of the line that passes through the two points.

y - y1 = m(x - x1)

y -1 = -6/7(x + 3)

y -1 = -6/7**x - 18/7

y = -6/7**x - 11/7

Question 54

Q

Find the equation of the line that

d) passes through (-4,0) and (0,3)

Answer

A

start by finding the gradient of the line

m = y₂-y₁/x₂-x₁
= 3-0/0+4
= 3/4

Now we can find the equation of the line that passes through the two points.

y - y₁ = m(x - x₁)
y - 0 = 3/4(x + 4)
y = 3/4**x + 3

Question 55

Q

Find the equation of the line that
e) passes through (1,8) and parallel to

𝑦 = 2/3**𝑥 + 4

Answer

A

If the line is parallel to y = 2/3**x + 4, then the gradient of the line will be 2/3

y - y1 = m(x - x1)
y - 8 = 2/3**(x - 1)
y - 8 = 2/3**x - 2/3
y = 2/3**x + 22/3

Question 56

Q

Find the equation of the line that

f) passes through (-2, -4) and parallel to 5𝑥 - 𝑦 + 1 = 0

Answer

A

We will start by finding the gradient of 5x - y + 1 = 0

5x - y + 1 = 0
y = 5x + 1

Therefore, the gradient is 5.

y - y1 = m(x - x1)
y + 4 = 5(x +2)

y +4 = 5x + 10

y = 5x + 6

Question 57

Q

g) passes through (5,1) and perpendicular to 3𝑥 + 2𝑦 = 0

Answer

A

We will start by finding the gradient of 3x + 2y = 0

3x + 2y = 0

2y = -3x

y = -3/2**x

Therefore, as the line we are trying to find it perpendicular to 3x+2y = 0, the gradient of the line we are trying to find must be 2/3.

(Remember the gradients of perpendicular
lines multiply to give -1).

y-y1=m(x-x1)

y - 1 = 2/3**(x-5)

y - 1 = 2/3**x - 10/3

y = 2/3**x - 7/3

Question 58

Q

Solve these simultaneous equations (then check your answers)

a)

-2𝑥 + 7𝑦 = 8
𝑦 + 1 = 3𝑥

Answer

A

-2x + 7y = 8 (1)
y + 1 = 3x (2)

Rearranging the second equation gives

-2x +7y = 8 (1)
3x -y = 1 (2)

To eliminate the y term, we will calculate (1) + 7 × (2).
19x = 15
x = 15/19
To find y, we will substitute x = 15/19 into Equation (2). (It doesn’t matter which equation is used to solve for y. Equation (2) was chosen as it appeared to be the
easiest to use to solve for y).
y + 1 = 3 × 15/19
y + 1 = 45/19
y = 26/19

Thus,

x = 15/19

y = 26/19

Question 59

Q

Solve these simultaneous equations (then check your answers)

b)

2𝑥 - 𝑦 - 11 = 0

4𝑥 + 𝑦 - 8 = 0

Answer

A

2x - y - 11 = 0 (1)
4x + y - 8 = 0 (2)
Simply adding Equations (1) and (2) will eliminate the y term

6x - 19 = 0

6x = 19

x = 19/6

to find y we will substitute x = 19/6 into Equation (1)

2 * 19/6 - y - 11 = 0

-y - 14/3 = 0

y = -14/3

Thus,

x = 19/6

y = -14/3

Question 60

Q

Solve these simultaneous equations (then check your answers)

c)

-3𝑥 + 𝑦 - 8 = 0

4𝑥 + 2𝑦 - 21 = 0

Answer

A

-3x + y - 8 = 0 (1)
4x + 2y - 21 = 0 (2)

To eliminate the y term, we will calculate 2 × (1) - (2).
-10x + 5 = 0
10x = 5
x = 1/2

To find y, we will substitute x = 1/2 into Equation (1)
-3 × 1/2 + y - 8 = 0
y - 19/2 = 0
y =19/2

Therefore,

x = 1/2
y = 19/2

Question 61

Q

Solve these simultaneous equations (then check your answers)

d)

4𝑥 - 7𝑦 = 21
6 = -2𝑥 + 𝑦

Answer

A

4x - 7y = 21 (1)
-2x + y = 6 (2)

To eliminate the x term, we will calculate (1) + 2 × (2)

-5y = 33

y = -33/5

To find x, we will substitute y = -33/5 into Equation (1).

4x - 7 * -33/5 = 21

4x + 231/5 = 21

4x = -126/5

x = -63/10

thus

x = -63/10

y = -33/5

Question 62

Q

a) fill in the table

b) Plot the 9 ordered pairs (𝑥, 𝑦) on the Cartesian plane
c) Draw a smooth curve through all 9 points
d) Calculate and draw in the line of symmetry
e) Label all 𝑥 and 𝑦 intercepts
f) Calculate and label the co-ordinates of the Turing Point.
g) State the Domain and Range of 𝑓(𝑥) = -𝑥² + 3𝑥 + 4

Answer

A

y = -x²+ 3x + 4

x -4 -3 -2 -1 0 1 2 3 4

y -24 -14 -6 0 4 6 6 4 0

(b) See graph below.
(c) See graph
(d) The line of symmetry is at x = 1.5. It is shown on the graph using a red, dashed line.
(e) See graph
(f) There is a turning point, a maximum, at (1.5, 6.25).
(g) Domain: All real values of x, Range: y ≤ 6.25

(a)

Question 63

Q

Use the Discriminant to determine the number of intercepts on the 𝑥 axis
a) 𝑦 = 3𝑥² + 4𝑥 - 1

Answer

A

To find the discriminant, D, of the quadratic y = ax² + bx + c, calculate D = b² - 4ac.

If the discriminant is positive (D>0), the quadratic has two x-intercepts.

If the discriminant is zero (D = 0), the quadratic only has one x-intercept.

If the discriminant is negative (D<0), the quadratic has no x-intercepts.

y = 3x<sup>2</sup> + 4x - 1
D = 4<sup>2</sup> - 4 × 3 × -1 = 28

As the discriminant is positive, the quadratic has two x-intercepts.

Question 64

Q

Use the Discriminant to determine the number of intercepts on the 𝑥 axis

b)

𝑦 = 𝑥² + 4𝑥 + 4

Answer

A

y = x<sup>2</sup> + 4x + 4
D = 4<sup>2</sup> - 4 × 1 × 4 = 0

As the discriminant is zero, the quadratic has one x-intercept.

Answer 62

A

y = -x² - 10x + 2
D = (-10)² - 4 × -1 × 2 = 108
As the discriminant is positive, the quadratic has two x-intercepts.

Answer 63

A

y = -2x² + x - 1
D = 1² - 4 × -2 × -1 = -7
As the discriminant is negative, the quadratic has no x-intercepts.

Answer 64

A

y = -x is drawn in blue
y = -2x is drawn in red
y = -2x + 3 is drawn in black

To draw a graph of y = -2x+3, it may be easier to just start with a graph of y = -2x.

Answer 65

A

y = x² is drawn in blue
y = 2x² is drawn in red

• y = 2x² - 4 is drawn in black
To draw a graph of y = 2x² -4, it may be easier to just start with a graph of y = 2x²

Answer 66

A

y = x² is drawn in blue
y = -1/4**x² is drawn in red
y = -1/4**x² + 2 is drawn in black

Answer 67

A

y = x² is drawn in blue
y = (x - 3)² is drawn in red
y = (x - 3)² + 1 is drawn in black

Answer 68

A

V (0) = 2 × 0² - 16 × 0 + 40
= 40
Initially (t = 0) there is 40 m³ of water in the tank

Answer 69

A

V (10) = 2 × 10² - 16 × 10 + 40
= 80

After 10 months (t = 10) there is 80 m³ of water in the tank.

Answer 70

A

To find the minimum volume in the tank over the first 10 months, we will start by drawing a graph of V (t).

From the graph, it can be seen that the minimum volume in the tank occurs at t = 4.

V (4) = 2 × 4² - 16 × 4 + 40
= 8
Alternatively, if we didn’t want to draw a graph, the x value of the turning point is given by
x = -b/2a
= 16/2*2
= 4

Thus the minimum volume in the tank over the 10 month period is 8 m³

Answer 71

A

To find the maximum volume in the tank over the 10 month period, we need to test the end points, t = 0 and t = 10.

The maximum volume will not occur at the turning
point as it was a minimum.

V (0) = 40 and V (10) = 80 (found in part (a)).

Therefore
the maximum volume of water in the tank over the 10 month period is 80 m³

Answer 72

A

The graph is a little hard to see, but we have the following information about the function h(d) where h is the height of the arch, in metres, above the water and d is the distance, in metres, across the river.

h(0) = 0
h(60) = 30
h(120) = 0

We have also been told that h(d) is a parabolic function (a quadratic).
Let h(d) = ad<sup>2</sup> + bd + c

where a, b and c are constants that we need to determine. Using h(0) = 0 gives
h(0) = a × 0² + b × 0 + c = 0
c = 0
Using h(120) = 0 gives
h(120) = a × 120² + b × 120 = 0
b × 120 = -a × 120²
b = -120a

Using h(60) = 30 and b = -120a gives
h(60) = a × 60<sup>2</sup> + b × 60 = 30
3600a + 60 × -120a = 30
3600a - 7200a = 30
-3600a = 30
a = -1/120

Finally, using b = -120a and that a = -1/120 gives

b = -120 * -1/120 = 1

Therefore, putting all the information together, the function h(d) is given by

h(d) = ad² + bd + c
= -1/120 × d² + 1 × d + 0
= -d²/120 + d