Binary Search Trees Flashcards
(37 cards)
What are the limitations of HashSets and the other data structures that we’ve seen so far in general?
There are additional operations that we may need to perform that other data structures cannot accomodate with O(1) efficiency such as:
- Retrieving elements in sorted order
- Determining the largest / smallest element
- Representing relationships between elements in the collection
What is a tree?
A data structure comprised of nodes in which each node has a value and links to zero or more child nodes. There is a single “root” node at the top of the tree.
What is a binary tree?
A binary tree is a type of tree where each node has exactly two children, a left and a right. Either or both children can be null. However, to qualify as a binary tree, every node must have at most one parent and there be exactly one node without a parent.
What is a binary search tree?
A data structure comprised of nodes and links in which values can be stored in a sorted order and each node has an associated value as well as links to two child nodes. The left child of a node always contains a smaller value and the right child contains a larger value than the parent node. Note: all the elements in the left sub-tree of a node are of lesser value than that node. Similarly, all elements in the right sub-tree of a node are of a higher value than that node.
What is a prerequisite for using a Binary Search Tree?
There must be a natural order to the elements so that they can be sorted. For example, the natural order of numbers is to store them in increasing order and the natural order of strings is alphabetic, or lexigraphic, order. For other objects, a class imposes natural order by implementing the Comparable interface and defining the CompareTo method.
What is a node?
In a tree, a node is a data object that is typically used as a building block. In a binary search tree a typical node contains fields for storing a value as well as links to two children (either or both of which can be null).
What is a leaf node?
In a tree, a node that has no children, in other words, both of its pointers point to null, is called a leaf node.
What is a root node?
In a tree, this is the topmost node of the tree. All other nodes are descendents of this node. In a balanced binary search tree this will typically be the median of the sorted set of values in the tree.
What is a child node?
In a tree, a child node is one that is pointed to by another node. That is, there is a link from another node pointing towards it.
What is a parent node?
In a tree, a node P that directly points to another node A is called its parent; P is the parent node of A.
What does it mean to “visit” a node on a tree?
To process the data stored in the node, such as printing it.
Inorder traversal
A strategy for traversing binary search trees in which we recursively traverse the left sub-tree, followed by the root, followed by the right subtree. This traversal method leads to visiting nodes in sorted order. Note that if we want to explore all the values of a BST in order, we perform inorder traversal.
How can you use inorder traversal to print the values of a binary search tree to print the values in sorted order?

Postorder traversal
A strategy for traversing binary search trees in which we recursively traverse the left sub-tree, followed by the right subtree, followed by the root.
Preorder traversal
A strategy for traversing binary search trees in which we recursively traverse the root, followed by the left sub-tree, followed by the right subtree.
How are binary search trees implemented in Java?
The Java collections framework implements binary search trees via the TreeSet class, which provides the following:
Constructors:
- TreeSet( ) - constructs a new, empty tree set, sorted according to the natural ordering of its elements
- TreeSet(Collection c) - constructs a new tree set containing the elements in the specified collection, sorted according to the natural ordering of its elements.
- TreeSet(Comparator comparator) - Constructs a new, empty tree set, sorted according to the specified comparator.
- TreeSet(SortedSet s) - Constructs a new tree set containing the same elements and using the same ordering as the specified sorted set.
Methods:
- add(E e) - adds the specified element to the set if it is not already present
- contains(Object o) - returns a boolean indicating whether the specified element is contained in the set
- remove(Object o) - removes the specified element from the set if it is present
- first( ) - returns the first (lowest) element currently in this set
- last( ) - returns the last (highest) element currently in this set
- pollFirst( ) - retrieves and removes the first (lowest) element, or returns null if this set is empty
- pollLast( ) - retrieves and removes the last (highest) element, or returns null if this set is empty
- floor(E e) - returns the greatest element in this set less than or equal to the given element, or null if there is no such element
- ceiling(E e) - returns the least element in this set greater than or equal to the given element, or null if there is no such element
- size( ) - returns the number of elements in this set (its cardinality)
- isEmpty( ) - returns true if this set contains no elements
Note that this is just a subset of the methods available. There are several others to extract a subset of elements. However it’s important to also note that as we saw with the HashSet class previously, there is no method to get, add, or remove a value by it’s index, since all of the values in a TreeSet are sorted by the elements’ natural order as opposed to being determined by the programmer.
How does the add method of the TreeSet work?
Like most operations on binary trees, adding a value to a binary search tree has a natural recursive implementation. The method
protected boolean add(Node n, E val)
adds the value to the tree rooted at Node n and returns true or false to indicate if it was successful. First, the method checks to see if the tree is empty, or null, and if so, creates and adds a new Node to the tree using the value provided. If it is not empty, then the method compares the value provided to the value in the root. If it’s less, then it’s added to the left subtree. If it’s greater, then it’s added to the right subtree.

How does the remove method of the TreeSet work?
To remove a value, you must locate the node that contains the value and remove it from the tree. There are 3 cases to consider:
- If the node has no children, then set the reference to it in its parent node to null.
- If the node has one child, then replace it with the child by updating the reference in its parent node.
- If the node has two children, then replace it with the largest value in its left subtree or the smallest value in the right subtree, which reduces this case to case 1 since the last node in that subtree will have no children.
Why would you use a TreeSet instead of HashSet?
You’d use a TreeSet instead of a HashSet if you need to work with elements in sorted order. Although you can insert elements into a HashSet more efficiently, they must be sorted each time they’re retrieved. Therefore, even though it may take more time to insert elements into the TreeSet, they’ll be retrieved in sorted order, eliminating the need keep subsequently sorting them.
What is a benefit of using a TreeSet over a HashSet?
TreeSet’s contains() function has a better worst case scenario than HashSet’s. That is, in the worst case, the contains() method for a TreeSet is O(log n) whereas the contains() method for a HashSet could take O(n) since as it becomes full it can devolve into a LinkedList.
What is the problem with just maintaining a sorted LinkedList?
Adding to a sorted LinkedList is a O(n) operation.
What is the output of the following snippet of code?

appled banana peach watermelon
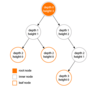
What is the “height” of a Binary Search Tree?
The length of the path from the deepest leaf node to the root of the tree. It is important to minimize the height of a BST in order for the contains, add, and remove operations to have logarithmic complexity. Otherwise, a BST can divulge into a linked list and have O(n) complexity.
Note that each node on the BST has a height as well. (The height of the tree is the height of the root node.) In the case of a node, it is the length of the path from it to a leaf node. A leaf node will have a height of 0.
What is the “depth” of a node on a Binary Search Tree?
The depth of a node is the length of the path from it to the tree’s root node. A root node will have a depth of 0. This is contrasted to the height in the following diagram: