Graphs Flashcards
(25 cards)
Graph
A data structure that stores relationships between elements in a collection. It consists of two main types of components: nodes (vertices) and edges connecting them. In a graph, each node can have an arbitrary number of edges to other nodes.
What is the difference between a relationship (stored in a graph) and an association (stored in a map)?
Maps can only store a single association (value) to a key. For example, a HashMap could be used to associate a city with it’s population, but it could not store the relationships between a city and multiple other cities such as distance.
Vertex
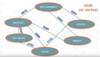
A vertex is a point on a graph that is also known as a junction. It is implemented with the same Node object used in linked lists and binary search trees. They generally contain some fields to store information about the elements contained in the graph. In the following example the Nodes contain names of cities that are stored in the graph:
Edge
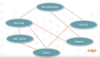
An object representing a link, or relationship, between two vertices (nodes) in a graph. These edges can be weighted (have some value attached to the link between two nodes) or unweighted. They can also be directed (point from one node to another) or undirected. Attributes such as weight and direction are typically stored as fields of the Edge object.
Weighted graph
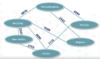
A graph in which all edges have an associated numerical value (weight). The opposite is an unweighted graph, in which all edges are assumed to have the same (or no) weight. In the following example, this weighted graph stores the distances between cities:
Degree of a node
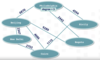
The number of each edges that a node has. In a directed graph these are split into in-degree (the number of edges pointing towards the node) and out-degree (the number of edges pointing away from the node). In the following example, the degree of the Node storing the city of Philadelphia is 3:
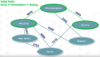
Path
In a graph, a path is a list of nodes from a start node to an end node in which each successive pair of nodes is connected by an edge. We frequently use paths to evaluate the relationships between elements in a collection. The simplest way is determining if an element is reachable from another. For example, the following example illustrates a valid path between cities in a graph:
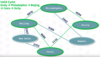
Cycle
A path of at least 3 nodes in which the start and end node are the same. For example, the following example illustrates a valid cycle between cities in a graph:
What is true of a valid cycle in a graph?
- The cycle’s start and end node are the same.
- It is also a valid path in the graph. (A path is defined as a list of nodes from a start node to an end node in which each successive pair of nodes is connected by an edge. The start and end nodes being the same does not violate the definition of a path.)
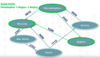
- The cycle can be directed or undirected. Remember: if the graph is directed, then any cycles that exist will also be directed. If the graph is undirected, then any existing cycles will also be undirected. That is, in a directed graph, a valid path or cycle must contain source/destination pairs. In the following example, there is a not a valid out-edge from Bejing to Philadephia so we cannot complete a valid cycle on that path.
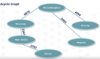
Cyclic / acyclic graph
A cyclic graph is a graph that contains at least one cycle. The opposite is an acyclic graph, which contains no cycles. The following example illustrates a acyclic graph:
Connected / disconnected graph
A connected graph is a graph in which all nodes are reachable from all other nodes (either directly or through some path in the graph). The opposite is a disconnected graph in which one or more nodes are not reachable from every other node. The following example illustrates a disconnected graph:
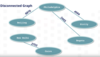
Connected component
A subgraph (part of a larger graph) in which each node is reachable from any other node in the same subgraph.
Directed / undirected graph
A directed graph is one in which the edges between nodes encode a specific direction to the relationship between the two nodes. The opposite is an undirected graph. The following example illustrates a directed graph:
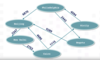
Source and destination nodes
In a directed graph, the source node is the origin of the path and the destination is the landing place. This is illustrated in the following example:
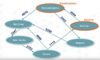
In / out edges
In a directed graph, an in-edge is an edge that points towards this node from another node. In contrast, an out-edge is an edge that points away from this node to another node. In the following example, the edge with weight 4594 is an out-edge from Sicily and and in-edge to Philadelphia.
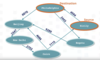
In degree/ out degree
The number of in-edges and/or out-edges of each node. This is illustrated in the following example:
How are graphs implemented in Java?
Unlike the other data structures that we’ve studied so far, there’s no standard implementation of a graph in the Java collections framework! In addition, there’s no one agreed upon “right” way to represent them in Java. However, there are generally 3 common ways to represent a graph in Java.
3 common graph representations
- Adjacency matrix - One of the common ways of representing a graph in code. It is a 2D array in which the value of [x, y] represents the weight of the edge from x to y. In an unweighted graph, it will typically be simply a 1 to indicate the presence of an edge.
- Edge set - Another common way to represent a graph in code. As the name suggests, it is a set of objects representing edges in the graph.
- Adjacency list - An efficient and general purpose implementation to represent a graph in code. The data structure is a map with the nodes as keys and a list of the nodes with which they share an edge (adjacent keys) as values. Given that there’s no implementation of a graph in the Java collections framework, this is the one that we’ll use in this course.
Adjacency list
The data structure is a map with the nodes as keys and a list of the nodes with which they share an edge (adjacent keys) as values. The list of nodes with which they share an edge is stored as {Source Node, Destination Node, Weight}. This is illustrated in the following example:

Neighbor
In a graph, a neighbor to a node A is any node that shares an edge with that node A. In a directed graph, a node is only considered a neighbor of node A if it is the destination node of one of the out-edges of node A. That is, a neighbor is any node that follows another in a path. The following code illustrates how to get all of the neighbors for a given node in a directed graph:

Breadth first search (BFS)
A graph traversal algorithm in which all immediate neighbors are visited before any more distant neighbors (e.g. neighbors of neighbors) are visited. That is, the nodes are visited horizontally, across the breadth of the graph, from left to right before visiting the next level down. The order in which the nodes are visited is typically maintained using a Queue in BFS implementations.
*Elaborate on this by specifying the complexity
Depth first search (DFS)
A graph traversal algorithm in which all unvisited neighbors of a node N are recursively visited before moving on to the next unvisited node in the graph and applying the same strategy.
*Elaborate on this by specifying the complexity!
Given an undirected graph G with n nodes, what is the minimum number of edges necessary for G to be connected?
For an undirected graph with n nodes to be connected, each node must have at least one edge connecting it to the other nodes in the graph, which gives us n edges. Then, since each edge actually connects two nodes, the minimum number of edges necessary to connect the graph is n - 1.
Given an undirected graph G with n nodes, what is the maximum number of edges possible for G if no nodes have self-loops (edges that connect a node to itself)?
The maximum number of edges in an undirected graph with no self-loops occurs when each node is directly connected to the remaining n - 1 nodes by an edge which gives n ( n - 1 ) edges. However, since this is an undirected graph an edge from A to B is equivalent to one from B to A. So, to remove the double-counted connections, we divide by 2 giving us n ( n - 1 ) / 2 as the maximum number of edges in an undirected graph.


