Heaps & Tries Flashcards
(15 cards)
What is a heap?
A heap is a complete or partially complete binary tree* in which the value of any node is always greater than that of its children, ensuring that the largest value node is the root of the tree. Therefore a heap enables us to quickly find the largest value in a collection since this can be done in O(1) time. Adding a value and removing the largest value can be done in O(log n) time.
*Note that a complete binary tree is a tree in which each node has exactly two children, a left and a right, either or both of which can be null. To qualify as a binary tree, every node must have at most one parent and there be exactly one node without a parent. To be a valid heap, every node doesn’t have to have two child nodes, but they must be added in the correct order such that the following example is a valid heap but if node 5 had a child and 11 didn’t, it’d be invalid since the nodes are in the wrong order.
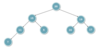
What is the heap property?
A heap satisfies the heap property: each node has a greater value than its children, and thus all of its descendants.
How do you implement a heap?
A heap can be implemented using array representation. This is therefore the first data structure that we’re encountering that has an implementation that doesn’t match the conceptual data structure!
The underlying array of the heap must abide by the following properties:
- A heap with max height h will have an array size of 2h - 1
- The root of the tree is in array index 0
- If a node is at index k
- Its left child is at index 2k+1
- Its right child is at index 2k+2
- Its parent is at index (k - 1) / 2
These relationships hold true because each level of the tree is filled before the next and each level of the tree is filled in from left to right with no gaps. This is represented as follows:
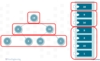
How many elements are in the bottom level of the following heap when represented in array form?
[18 14 16 13 9 12 10 11 4 6 7 8]
5
How do you add a value to a heap?
In order to satisfy the properties of a heap, you must add the new value by placing it in the next available spot in the complete binary tree (as shown below). The value then “bubbles up” as long as it is greater than its parent’s value so that it is stored in the correct position.

How do you remove a value from a heap?
You can only remove the largest value from a heap, which is the root. However, after removing the root you need to join the two separate subtrees. This is done by replacing the missing root with the last value in the heap’s underlying array (at index position size - 1). This value then “bubbles down” until it’s in the correct place and the largest value is in the root position. This is done by comparing the root to each of its children and swapping them as needed, which can be done concisely with recursion.
How are heaps implemented in the Java API?
In the Java API, they are implemented as Priority Queues: java.util.PriorityQueue<e>. This class implements a Min-Heap in which the smallest value is at top of tree in contrast to the Max-Heap examples that we've seen so far. Although the queue data structure is based on a linked list and the priority queue is based on a heap, the priority queue still abides by the same property that a value can only be removed from the front or top of the queue and added to the back or end. However, it has an additional property of the top value always being the smallest which is its priority. </e>
This class provides the following methods:
- add(Element) : inserts element into heap
- remove( ) : retrieves and removes root of the heap (minimum value; “head” of the “priority queue”)
- peek( ) : retrieves but does not remove root of the heap
Note that the add and remove methods are O(log2n); peek is O(1).
Why is a binary search tree less efficient storing strings?
Given that strings are compared lexigraphically, more than one comparison is needed if they start with the same letter. Therefore comparing the values in 2 nodes may take 2, 3, 4, 4, 6, etc. comparisons. This is illustrated in the following diagram:

What is a trie?
A trie is a tree based data structure that efficiently stores strings in order to support fast pattern matching. In a trie each node holds a single character and the concatenation of the characters stored in all subsequent nodes on any path from it to a leaf yields a string in collection. That is, reading each letter of a node on the path from the root to a leaf produces a word.
It satisfies the following properties:
- Each node, except the root is labeled with a character from the alphabet (the root is always empty!)
- The children of an internal node have distinct labels (i.e. letters are not stored more than once)
- Each leaf node is associated with a string, such that the concatenation of the labels of the nodes on the path from root to leaf yields that particular string
Note the additional properties of a trie:
- The height is equal to the length of the longest string stored
- The number of children of each internal node is at most the number of characters in the alphabet
- The number of leaves is equal to the number of strings
- The number of nodes is at most n+1 where n is the total length of all strings
The following diagram is an example in which you can see it does not have the same properties as a binary search tree. That is, a node can have more than 2 children, the nodes are not in size order, etc.
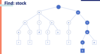
How do you find a string to a trie?
You start at the root and look for a child node that contains the first letter of the word. If there is a match, then you continue to traverse the tree comparing the child nodes to each subsequent letter of the word until the full match is found. The following diagram illustrates an example:
How do you add a string to a trie?
Follow a path from the root of the trie that contains as many letters in the string as possible and then add as many remaining characters as needed.
How do you add a string to a trie if one of its paths already contains that word? (i.e. the word is a prefix or another such as sun in sunshine or be in bell)
You terminate that prefix with a null value to indicate that it is a unique word in the tree as well:
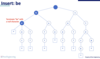
How do you delete an element from a trie?
You begin the same way as finding a node: You start at the root and look for a child node that contains the first letter of the word. If there is a match, then you continue to traverse the tree comparing the child nodes to each subsequent letter of the word until the full match is found. Note that that you DO NOT delete each character as it’s found. Instead, you locate the entire word in the trie and then delete characters one by one as long as they do not have any children. That is, as long as they are not used in any other words. This is important characters can be present in more than one word in the trie! This means that deleting a word does not require deleting every letter of which it’s comprised!
For example, to delete the word “BID” in the following trie, you locate the full word, delete the letter D, and then delete the letter I.
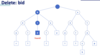
What is the complexity of trie operations?
The complexity of trie operations is a function of the number of letters in a given string as opposed to the number of elements in the collection. We express this as O(m) where m is the length of the string. However, this requires each node to store its child nodes in an O(1) data structure such as a hash set so that it can be located in one comparison as opposed to checking each letter of the alphabet in the worst case scenario, which would have O(m ∙ |Σ| ) complexity. This is illustrated in the following example:
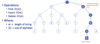
Which of the following are true of a standard trie containing n strings of m maximum length using an s sized alphabet? (Assume that all strings are null-terminated.)
- Each node is labeled with a character from the alphabet
- The height of the tree is n
- The maximum number of children of each internal node is at most s+1
- The number of leaves of the tree is equal to n
- The find, insert, and delete operations can be optimized to O(m)
- Each node is labeled with a character from the alphabet - FALSE, the root is always empty
- The height of the tree is n - FALSE, the height is equal to the longest string, not the number of strings in the collection
- The maximum number of children of each internal node is at most s + 1 - TRUE, the plus 1 accounts for the null-terminating node
- The number of leaves of the tree is equal to n - TRUE, since the paths from root to leaf represent a full string the number of leaves should be equal to the number of strings.
- The find, insert, and delete operations can be optimized to O(m) - TRUE, as long as each node stores its children in an O(1) data structure such as a hash set


