Math Flashcards
The concept from economics and game theory addressing dynamics of a non-cooperative game, referring to a situation in which players in a game pursue the optimal strategy while knowing the other players’ strategies, is commonly named after what mathematician and Nobel laureate?
John Forbes Nash Jr.
A posthumous paper by mathematician August Ferdinand Möbius explores the properties of one-sided surfaces via a strip, connected at the ends with a half-twist in the middle. Fellow German mathematician Felix Klein pursued a similar illustration using a theoretical surface that is today, perhaps due to a mistranslation of the original German, most commonly referred to as what type of object?
Bottle
What metric unit of area is roughly equal to 2.47 acres in the U.S. customary system?
Hectare
First proposed in the 1860s and controversial at the time, the scientific laws known as the law of segregation, the law of independent assortment, and the law of dominance are known collectively as a set of laws named after what Augustinian friar?
Gregor Mendel
While a quadrilateral with at least one pair of parallel sides is known in North America as a trapezoid, outside North America it is known as what? The term in question, to North Americans, describes a quadrilateral with no parallel sides (which, outside North America, is simply called a general irregular quadrilateral).
Trapezium
A historically significant mathematics problem, asking, essentially, if a graph on four nodes with seven edges has a “Eulerian path,” was answered in the negative (by Leonhard Euler himself) using the seven bridges of what Prussian city?
Konigsberg
In his Elements, Euclid states five postulates of plane geometry. Four of them are considered fundamental, and apply in many non-Euclidean geometries as well. What geometric term is typically used to name the fifth postulate, despite Euclid not using the word in the postulate’s description?
Parallel
This is the name of the division sign.
Obelus
British mathematician Charles Hinton was known for coining this term, used to describe a shape in the fourth dimension.
Tesseract
What is the term in mathematics for a positive integer that is equal to the sum of its proper divisors (i.e., its divisors not including the number itself)? The first such number is 6 (1+2+3); the next four are 28, 496, 8,128, and 33,550,336.
Perfect number
Among the named properties of equalities in mathematics are the transitive property (if a=b and b=c, then a=c), the symmetric property (if a=b, then b=a), and what other property, which states that any quantity is equal to itself (a=a)?
Reflexive Property
“No three positive integers a, b, and c satisfy the equation a^n + b^n = c^n for any integer value of n greater than 2.” This mathematical statement is associated with British mathematician and Oxford professor Sir Andrew Wiles, but even moreso with what Frenchman?
Pierre de Fermat
99/70 (“Ninety-nine seventieths”) is a frequently used rational approximation for an irrational number that is most commonly referred to as what?
Square root of two
The cube is one of the 5 “platonic solids” or regular these.
Polyhedra
In mathematics, the best-known and most commonly used coordinate system for identifying a point in a plane is named after what man, who invented it in the 17th century?
Rene Descartes
Whose “witch” is pictured here?
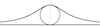
(Maria Gaetana) Agnesi
What term can be used in geometry for the region of a circle bounded by an arc of the circle and a chord that connects the endpoints of the arc, and also for the portion of a sphere included between a pair of parallel planes that intersect the sphere? Note, while these are common uses of the term in question in geometry, they are not the most common.
Segmemt
This geometric shape is the portion of a solid (normally a cone or pyramid) that lies between one or two parallel planes cutting it. A “right” version of this shape is a parallel truncation of a right pyramid or right cone.
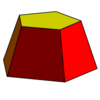
Frustum
In 1952 an early computer was used to discover the thirteenth Mersenne one of these numbers.
Prime
What is a fractal?
A curve or geometric figure, each part of which has the same statistical character as the whole. Fractals are useful in modeling structures in which similar patterns recur at progressively smaller scales, and in describing partly random or chaotic phenomena such as crystal growth, fluid turbulence and galaxy formation.
A quadrant is a circular measure equal to this many degrees.
90
What term in mathematics most commonly represents the set of all values that a given function’s independent variable (e.g. “x” in y=2x) can have?
Domain
What branch of mathematics, which dates back to 1874, is based on binary operators like union, intersection, and Cartesian product?
Arithmetic has addition, subtraction and so on; unions and intersections are from set theory.
What is the term for the mathematical property, applicable to addition and multiplication (but not subtraction or division), that states that a given operation’s result is independent of the order of the numbers/objects in the operation? For example, 3 + 5 = 5 + 3 and 2 x 6 = 6 x 2.
Commutative
What term is most often used to refer to all numbers that can be represented on the number line? The complete set includes all natural numbers, whole numbers, integers, rational numbers, and irrational numbers.
Real Numbers
All of the faces of a polyhedron known as a regular dodecahedron are what shape?
(Regular) Pentagon
It is as yet an unproven conjecture that there exist infinitely many pairs of primes that differ by two. These special prime numbers (e.g., 17 and 19, or 1019 and 1021) are sometimes known as “prime pairs” but are best known as what?
Twin Primes
What mathematical term is used to designate a trapezoid (in the UK, a trapezium) having its two non-parallel sides of equal length? Such a shape is also sometimes referred to as a regular trapezoid.
Isoceles
What kind of logic gate produces a true output only when exactly one of its inputs is true?
XOR (Exclusive OR)
In statistics, a series of random events in which the probability of a given event is determined only by its predecessors is known as a “chain” named after what Russian mathematician?
Andrei Markov
It’s the term for a chord that goes through the center of a circle.
Diameter
What rule of logical inference, sometimes called implication elimination, is abbreviated “MP”?
Modus ponens is Latin for “method of affirming.” The rule holds that, if p implies q, and we know p is true, then so is q. Um, no duh!
In mathematics, what is denoted by this symbol: ≅?
Congruent
From the Latin for “cushion”, what word describes the 3-dimensional shape known colloquially as a doughnut shape?
Torus
The statement that, for all integers n > 2, the equation xn + yn = zn has no positive integer solutions was proven in 1994 by Andrew Wiles, but is most often associated with (and named after) what other mathematician?
Pierre de Fermat
My Dear Aunt Sally can help you learn the order of these mathematical processes, which include addition, subtraction, division, and multiplication, among others. What name is given to these processes?
Operations
Besides 1, what’s the first number in a Fibonacci sequence that’s also a perfect square?
144
In 1882, what German mathematician described a one-sided “surface,” or “Fläche,” that was later called a “Flasche,” meaning “bottle”?
Yup, Dr. Felix Klein’s namesake “Klein bottle” may be a mistranslation of “Klein surface.”
What is the most common term used for a number defined as a real number that cannot be expressed as a ratio between two integers (i.e., it has an infinite number of non-repeating digits to the right of the decimal point)?
Irrational
This non-imperial measure was originally defined as one 10-millionth the distance from the North Pole to the equator
Meter
What word was coined by French mathematician Benoit Mandelbrot to refer to an irregular pattern that’s self-similar in scale (i.e., where any section resembles the whole)?
Fractal
The mathematical constant pi (π) is commonly defined as the ratio of the a of a circle to its b. What two words, in order, correctly replace a and b in the preceding sentence?
Circumference, Diameter
What unit of measurement of angles is equal to approximately 57.296 degrees? Exactly π/2 of this unit equals a right angle.
Radians
Arab mathematician and astronomer Muhammad ibn-Musa al-Khwarizmi, who compiled early works on arithmetic and astronomical tables, introduced algebraic concepts to Western mathematics as a result of his work’s translation into Latin. In fact, it is from the Latinization of his name that what common word in mathematics is derived?
Algorithm
The symbol known as the cap symbol, such as in the expression A ∩ B, is used in mathematics to represent the operation most often given what name?
Intersection
In mathematics, the sum of a real number and an imaginary number, expressed typically as x + iy or a + bi, is referred to most often as what kind of number?
Complex Number
